2024年浙教版数学八(下)微素养核心突破24 反比例函数与一次函数综合
试卷更新日期:2024-06-01 类型:复习试卷
一、选择题
-
1. 如图,一次函数与反比例函数的图象相交于A,B两点,点A的横坐标为2,点B的横坐标为 , 则不等式的解集是( )
 A、或 B、或 C、或 D、2. 如图,反比例函数的图象与一次函数的图象相交于点 , , 则不等式的解是( )
A、或 B、或 C、或 D、2. 如图,反比例函数的图象与一次函数的图象相交于点 , , 则不等式的解是( ) A、或 B、或 C、或x>2 D、或3. 在平面直角坐标系xOy中,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y=相交于点A,B,且AC+BC=4,则△OAB的面积为( )A、2+或2- B、2+2或2-2 C、2- D、2+24. 如图,反比例函数和正比例函数的图象相交于A(-1,-3),B(1,3)两点.若则x的取值范围是( )
A、或 B、或 C、或x>2 D、或3. 在平面直角坐标系xOy中,直线AB垂直于x轴于点C(点C在原点的右侧),并分别与直线y=x和双曲线y=相交于点A,B,且AC+BC=4,则△OAB的面积为( )A、2+或2- B、2+2或2-2 C、2- D、2+24. 如图,反比例函数和正比例函数的图象相交于A(-1,-3),B(1,3)两点.若则x的取值范围是( )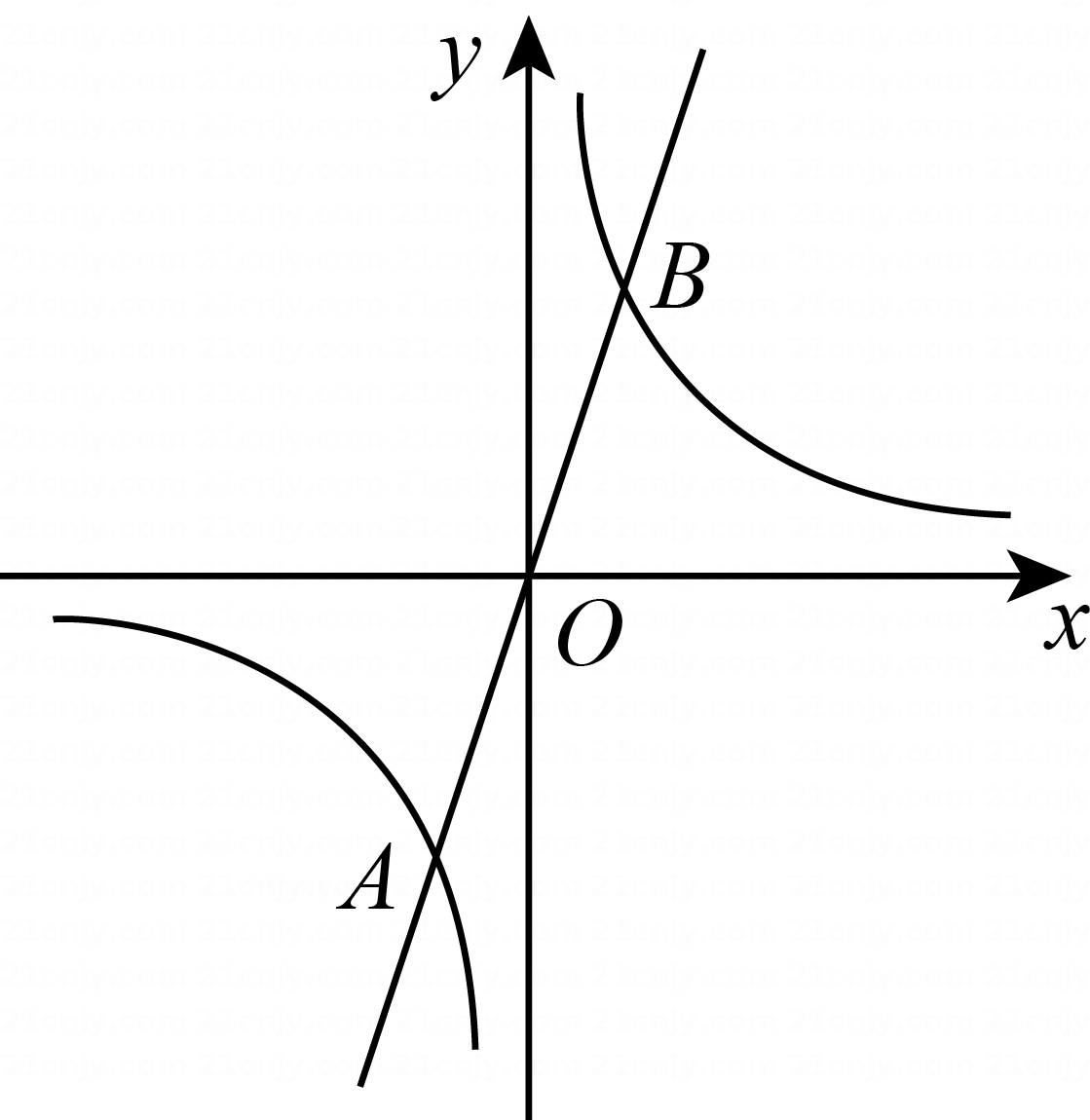 A、1<x<0 B、1<x<1 C、x<1或0<x<1 D、1<x<0或x>15. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数的图象上,点D的坐标为(4,3).若将菱形ABCD沿x轴正方向平移,则当菱形的顶点D落在函数的图象上时,菱形ABCD沿x轴正方向平移的距离为( )
A、1<x<0 B、1<x<1 C、x<1或0<x<1 D、1<x<0或x>15. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数的图象上,点D的坐标为(4,3).若将菱形ABCD沿x轴正方向平移,则当菱形的顶点D落在函数的图象上时,菱形ABCD沿x轴正方向平移的距离为( ) A、3 B、5 C、 D、86. 如图,一次函数y=ax+b(a≠0)与反比例函数y 的图象相交于点A(1,2),B(m,-1),则关于x的不等式 的解是( )
A、3 B、5 C、 D、86. 如图,一次函数y=ax+b(a≠0)与反比例函数y 的图象相交于点A(1,2),B(m,-1),则关于x的不等式 的解是( ) A、x<-2或0<x<1 B、x<-1或0<x<2 C、-2<x<0或x>1 D、-1<x<0或x>27. 函数和y=-kx+2(k≠0); 在同一平面直角坐标系中的图象可能是 ( )A、
A、x<-2或0<x<1 B、x<-1或0<x<2 C、-2<x<0或x>1 D、-1<x<0或x>27. 函数和y=-kx+2(k≠0); 在同一平面直角坐标系中的图象可能是 ( )A、 B、
B、 C、
C、 D、
D、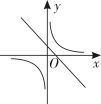 8. 已知关于x的一元二次方程 , 及函数 , (a,b,c为常数,且),则( )A、若方程有解,则函数的图象一定有交点 B、若方程有解,则函数的图象一定没有交点 C、若方程无解,则函数的图象一定有交点 D、若方程无解,则函数的图象一定没有交点9. 反比例函数图像上有两个点 , , , 则的图像不经过第( )象限A、一 B、二 C、三 D、四10. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( )
8. 已知关于x的一元二次方程 , 及函数 , (a,b,c为常数,且),则( )A、若方程有解,则函数的图象一定有交点 B、若方程有解,则函数的图象一定没有交点 C、若方程无解,则函数的图象一定有交点 D、若方程无解,则函数的图象一定没有交点9. 反比例函数图像上有两个点 , , , 则的图像不经过第( )象限A、一 B、二 C、三 D、四10. 如图,一次函数与反比例函数的图像相交于A、B两点,与x轴,y轴分别相交于C、D两点,连接OA、OB.过点A作轴于点 , 交于点 . 设点A的横坐标为 . 若 , 则的值为( ) A、1 B、 C、2 D、4
A、1 B、 C、2 D、4二、填空题
-
11. 如图,在平面直角坐标系中,直线y1=k1x+b与双曲线y2=(其中k1 , k2≠0)相交于A(-2,3),B(m,-2)两点,过点B作BP∥x轴,交y轴于点P,则△ABP的面积是
 12. 如图,矩形ABCD的边AB与y轴平行,已知点A(1,m),C(3,m+6),则图象同时经过点B与点D的反比例函数的表达式为.
12. 如图,矩形ABCD的边AB与y轴平行,已知点A(1,m),C(3,m+6),则图象同时经过点B与点D的反比例函数的表达式为. 13. 若在反比例函数的图象的每一分支上,y都随x的增大而减小,且整式是一个完全平方式,则该反比例函数的表达式为.
13. 若在反比例函数的图象的每一分支上,y都随x的增大而减小,且整式是一个完全平方式,则该反比例函数的表达式为. 14. 如图,正比例函数:y=ax(a≠0)的图象与反比例函数的图象相交于点A,B.若点A的坐标为(2,3),则点B的坐标为.
14. 如图,正比例函数:y=ax(a≠0)的图象与反比例函数的图象相交于点A,B.若点A的坐标为(2,3),则点B的坐标为.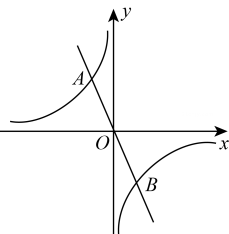 15. 如图,一次函数(和均为常数且与反比例函数为常数且的图象交于A,B两点,其横坐标分别为1和2.5,则关于的不等式的解集是.
15. 如图,一次函数(和均为常数且与反比例函数为常数且的图象交于A,B两点,其横坐标分别为1和2.5,则关于的不等式的解集是. 16. 如图,在平面直角坐标系xOy中,直线y=kx(k <0)与反比例函数的图象相交于A,C两点,D为x轴负半轴上一点,连结CD 并延长,交反比例函数 的图象于点B.若CB =2CD,△CDO的面积为1,则m-n=.
16. 如图,在平面直角坐标系xOy中,直线y=kx(k <0)与反比例函数的图象相交于A,C两点,D为x轴负半轴上一点,连结CD 并延长,交反比例函数 的图象于点B.若CB =2CD,△CDO的面积为1,则m-n=.
三、综合题
-
17. 已知:如图,在平面直角坐标系中,一次函数 与反比例函数 的图象交于点 和点 ,与 轴交于点 ,
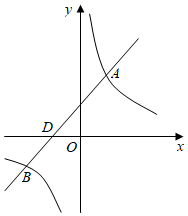 (1)、求 的值及点 的坐标;(2)、写出 时 的取值范围;(3)、 是 轴上一点,且满足 的面积等于 .求点 坐标.18. 如图,四边形ABCD的四个顶点分别在反比例函数与的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4.
(1)、求 的值及点 的坐标;(2)、写出 时 的取值范围;(3)、 是 轴上一点,且满足 的面积等于 .求点 坐标.18. 如图,四边形ABCD的四个顶点分别在反比例函数与的图象上,对角线BD∥y轴,且BD⊥AC于点P.已知点B的横坐标为4. (1)、当m=4,n=20时,
(1)、当m=4,n=20时,①若点P的纵坐标为2,求直线AB的函数表达式.
②若P是BD的中点,试判断四边形ABCD的形状,并说明理由.
(2)、四边形ABCD能否为正方形?若能,求此时m,n之间的数量关系;若不能,请说明理由.19. 已知一次函数y=2x-1和反比例函数的图象的一个交点的坐标为(1,a).(1)、求反比例函数的表达式.(2)、若这两个函数图象的另一个交点为A,求点A的坐标.
(3)、在(2)的条件下,若点B的坐标为(2,0),且以A,O,B,P为顶点的四边形是平行四边形,请你直接写出点P的坐标.20. 如图,在平面直角坐标系中,已知一次函数的图象与坐标轴分别相交于A(5,0),B.(0,)两点,且与反比例函数的图象在第一象限内相交于P,K两点,连结OP,△OAP的面积为. (1)、求一次函数与反比例函数的表达式.(2)、当y₂>y₁时,求x的取值范围.(3)、若C为线段OA上的一个动点,当PC+KC的值最小时,求△PKC的面积.21. 如图,在平面直角坐标系 xOy中,一次函数y =ax+b(a≠0)的图象与反比例函数≠0)的图象相交于 P,Q两点,点 P(-4,3),点 Q 的纵坐标为-2.求:
(1)、求一次函数与反比例函数的表达式.(2)、当y₂>y₁时,求x的取值范围.(3)、若C为线段OA上的一个动点,当PC+KC的值最小时,求△PKC的面积.21. 如图,在平面直角坐标系 xOy中,一次函数y =ax+b(a≠0)的图象与反比例函数≠0)的图象相交于 P,Q两点,点 P(-4,3),点 Q 的纵坐标为-2.求: (1)、反比例函数与一次函数的表达式.(2)、△POQ的面积.22. 已知一次函数y=kx+b(k≠0)的图象与反比例函数 的图象相交于点A(1,m),B(n,-2).
(1)、反比例函数与一次函数的表达式.(2)、△POQ的面积.22. 已知一次函数y=kx+b(k≠0)的图象与反比例函数 的图象相交于点A(1,m),B(n,-2). (1)、求一次函数的表达式,并在如图所示的直角坐标系中画出这个一次函数的图象.(2)、根据(1)中的函数图象,直接写出不等式 的解.(3)、若点 C 是点 B 关于 y 轴的对称点,连结AC,BC,求△ABC的面积.23. 如图,菱形的边在轴上,点A的坐标为 , 点在反比例函数的图象上,直线经过点 , 与轴交于点 , 连接 .
(1)、求一次函数的表达式,并在如图所示的直角坐标系中画出这个一次函数的图象.(2)、根据(1)中的函数图象,直接写出不等式 的解.(3)、若点 C 是点 B 关于 y 轴的对称点,连结AC,BC,求△ABC的面积.23. 如图,菱形的边在轴上,点A的坐标为 , 点在反比例函数的图象上,直线经过点 , 与轴交于点 , 连接 . (1)、求的值.(2)、求的面积.(3)、已知点在反比例函数的图象上,点的横坐标为 . 若 , 则的取值范围为 .24. 如图,正比例函数 的图象与反比例函数 的图象都经过点 A(a,2).
(1)、求的值.(2)、求的面积.(3)、已知点在反比例函数的图象上,点的横坐标为 . 若 , 则的取值范围为 .24. 如图,正比例函数 的图象与反比例函数 的图象都经过点 A(a,2). (1)、求点 A 的坐标和反比例函数的表达式.(2)、若点 P(m,n)在该反比例函数的图象上,且它到 y轴的距离小于 3,请根据图象直接写出 n的取值范围.25. 如图,一次函数图象与反比例函数图象交于点A(-1,6),B( , a-3),与x轴交于点C,与y轴交于点D.
(1)、求点 A 的坐标和反比例函数的表达式.(2)、若点 P(m,n)在该反比例函数的图象上,且它到 y轴的距离小于 3,请根据图象直接写出 n的取值范围.25. 如图,一次函数图象与反比例函数图象交于点A(-1,6),B( , a-3),与x轴交于点C,与y轴交于点D. (1)、求反比例函数与一次函数的表达式;(2)、点M在x轴上,若S△OAM=S△OAB , 求点M的坐标.26. 设函数 函数 (k1、k2、b是常熟,k1≠0,k2≠0).(1)、若函数y1和函数 y₂的图象相交于点 A (1,m),B(3,1),
(1)、求反比例函数与一次函数的表达式;(2)、点M在x轴上,若S△OAM=S△OAB , 求点M的坐标.26. 设函数 函数 (k1、k2、b是常熟,k1≠0,k2≠0).(1)、若函数y1和函数 y₂的图象相交于点 A (1,m),B(3,1),①求函数 y₁,y₂ 的表达式.
②当2<x<3时,比较 y₁ 与y₂的大小(直接写出结果).
(2)、若点 C(2,n)在函数 y₁ 的图像上,点 C 先向下平移 2个单位,再向左平移4 个单位,得点D.若点 D 恰好落在函数 y₁ 的图像上,求 n 的值.四、实践探究题
-
27. 阅读材料:
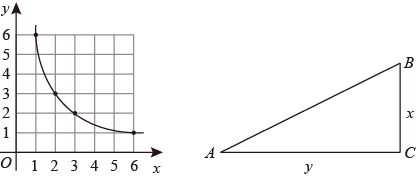
已知:一次函数y=﹣x+b与反比例函数y= (x>0),当两个函数的图象有交点时,求b的取值范围.
 (1)、方方给出了下列解答:
(1)、方方给出了下列解答:﹣x+b=
x2﹣bx+4=0
∵两个函数有交点
∴△=b2﹣16≥0
但是方方遇到了困难:利用已学的知识无法解b2﹣16≥0这个不等式;
此时,圆圆提供了另一种解题思路;
第1步:先求出两个函数图象只有一个交点时,b= ▲ ;
第2步:画出只有一个交点时两函数的图象(请帮圆圆在直角坐标系中画出图象);
第3步:通过平移y=﹣x+b的图象,观察得出两个函数的图象有交点时b的取值范围是 ▲ .
应用:
如图,Rt△ABC中,∠C=90°,BC的长为x,AC的长为y,且S△ABC=12.
(2)、求y关于x的函数表达式;(3)、设x+y=m,求m的取值范围.