2024年浙教版数学八（下）微素养核心突破21图形变换（2）：动点问题

试卷更新日期：2024-06-01 类型：复习试卷

进入出卷网下载

一、选择题

1. 如图①，在四边形 $A B C D$ 中， $B C ∥ A D$ ， $∠ A = 90 °$ ，点P从点A出发，沿 $A \to B \to C \to D$ 运动到点D．图②是点P运动时， $△ P A D$ 的面积S与点P运动的路程x之间的关系图象，则a的值为（　　）

A、 $\frac{7}{2}$ B、4 C、5 D、6

查看试题解析
2. 如图， $▱$ ABCD中，AB=22cm，BC= $8 \sqrt{2}$ cm，∠A=45°，动点E从A出发，以2cm/s的速度沿AB向点B运动，动点F从点C出发，以1cm/s的速度沿着CD向D运动，当点E到达点B时，两个点同时停止．则EF的长为10cm时点E的运动时间是（）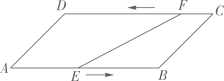

A、6s B、6s或10s C、8s D、8s或12s

查看试题解析
3. 如图（1），在 $□ A B C D$ 中， $A B > B C$ ， $∠ A B C = 150 °$ ，动点P从点B出发，沿 $B \to C \to D \to A$ 匀速运动，设点P运动的路程为x ， $△ A B P$ 的面积为y（当A ， B ， P点共线时，不妨设 $y = 0$ ），y与x之间的函数关系的图象如图（2）所示，则图（2）中a的值为（）

A、16 B、15 C、14 D、13

查看试题解析
4. 如图，在正方形ABCD中，AB=4，E是边BC上的一点且CE=3，连结DE，动点M从点A以每秒2个单位的速度沿AB—BC—CD—DA向终点A运动.设点M的运动时间为t秒，当△ABM和△DCE全等时，t的值为（）

A、3.5 B、4.5 C、3.5或5.5 D、3.5或6.5

查看试题解析
5. 如图，在菱形ABCD中，AB=5cm，∠ADC=120°，点E，F同时从A，C两点出发，分别沿AB，CB方向向点B匀速移动(到点B为止)，点E的速度为1 cm/s，点F的速度为2cm/s，经过t(s)△DEF是等边三角形，则t的值为（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{2}$ D、 $\frac{5}{3}$

查看试题解析
6. 对于题目，“在长为 $7$ 的线段 $A E$ 上取一点 $B$ ，使 $A B = 3$ ，以 $A B$ 为边向上作矩形 $A B C D$ ，且 $A D = 2$ ，点 $N$ 从点 $D$ 出发，沿射线 $D C$ 方向以每秒 $2$ 个单位长的速度运动，点 $M$ 从点 $E$ 出发，先以每秒 $1$ 个单位长的速度向点 $B$ 运动，到达点 $B$ 后，再以每秒 $3$ 个单位长的速度沿射线 $B E$ 方向运动，已知 $M$ 、 $N$ 同时出发，运动时间为 $t (s)$ ，若以 $E$ 、 $M$ 、 $C$ ， $N$ 为顶点的四边形是平行四边形，求 $t$ 的值”，甲答： $1$ ，乙答， $3 .$ （）

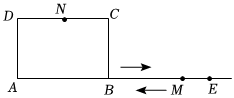A、只有甲答的对 B、只有乙答的对 C、甲、乙答案合在一起才完整 D、甲、乙答案合在一起也不完整

查看试题解析
7. 如图1，点 $F$ 从四条边都相等的 $▱ A B C D$ 的顶点 $A$ 出发，沿 $A \to D \to B$ 以 $1 c m / s$ 的速度匀速运动到点 $B$ ，图2是点 $F$ 运动时， $△ F B C$ 的面积 $y (c m^{2})$ 随时间 $x (s)$ 变化的关系图象，则 $a$ 的值为（）

A、 $\sqrt{5}$ B、 $2$ C、 $\frac{5}{2}$ D、 $2 \sqrt{5}$

查看试题解析
8. 如图，正方形 $A B C D$ 的边长为8，M在 $C D$ 上，且 $D M = 2$ ， N是 $A C$ 上的一个动点，则 $D N + M N$ 的最小值为（）

A、6 B、8 C、10 D、 $8 \sqrt{2}$

查看试题解析
9. 如图，在矩形ABCD中，O为对角线BD的中点，∠ABD=60°，动点E在线段OB上，动点F在线段OD上，点E，F同时从点O出发，分别向终点B，D运动，且始终保持OE=OF．点E关于AD ，AB的对称点为E₁ ， E₂；点F关于BC，CD的对称点为F₁ ， F₂_，在整个过程中，四边形E₁E₂F₁F₂形状的变化依次是（）

A、菱形→平行四边形→矩形→平行四边形→菱形 B、菱形→正方形→平行四边形→菱形→平行四边形 C、平行四边形→矩形→平行四边形→菱形→平行四边形 D、平行四边形→菱形→正方形→平行四边形→菱形

查看试题解析

二、填空题

10. 如图，已知 $O A = 4$ ， $O C = 8$ ，点P从原点O出发，以每秒1个单位长度的速度沿着长方形 $O A B C$ 移动一周（即：沿着 $O \to A \to B \to C \to O$ 的路线移动），在移动过程中，当点P移动的时间为秒，点P与点A之间的距离为5．

查看试题解析
11. 如图，在等边 $△ A B C$ 中， $A B = 5 c m$ ，射线 $A G ∥ B C$ ，点 $E$ 从点 $A$ 出发沿射线 $A G$ 以 $1 c m / s$ 速度运动，点 $F$ 从点 $C$ 出发沿射线 $C B$ 以 $2 c m / s$ 的速度运动．如果点 $E ， F$ 同时出发，设运动时间为 $t (s)$ ，则当 $t =$ $s$ 时，以 $A ， E ， F ， B$ 为顶点的四边形是平行四边形．

查看试题解析
12. 如图，菱形ABCD的对角线AC， BD相交于点O，P为AB边上一动点（不与点A，B重合），PE⊥OA于点E，PF⊥OB于点F，若AB=8，∠BAD=60°，则线段EF长度的最小值为．

查看试题解析
13. 如图，在等边三角形 $A B C$ 中， $B C = 6 c m$ ，射线 $A G / / B C$ ，点 $E$ 从点 $A$ 出发沿射线 $A G$ 以 $1 c m / s$ 的速度运动，点 $F$ 从点 $B$ 出发沿射线 $B C$ 以 $2 c m / s$ 的速度运动.如果点 $E, F$ 同时出发，设运动时间为 $t (s)$ .当 $t =$ 时，以 $A ， C ， E ， F$ 为顶点的四边形是平行四边形.

查看试题解析
14. 如图，菱形 $A B C D$ 的边长为 $4 ， ∠ D A B = 60 °$ ，点E为 $B C$ 边的中点，点P为对角线 $A C$ 上一动点，则 $P B + P E$ 的最小值为．

查看试题解析
15. 如图，矩形 $A B C D$ 中， $A B = 8 c m$ ， $B C = 12 c m$ ，动点 $P$ 从点 $A$ 出发沿 $A - B - C - D - A$ 运动，速度是 $2 c m$ /秒；点 $Q$ 从点 $C$ 出发沿 $C - B - A - D - C$ 运动，速度是 $4 c m$ /秒，设它们的运动时间为 $t$ 秒．

(1)、当 $t = 1$ 时，连接 $P Q$ ， $P Q =$ $c m$ ；

(2)、若 $P$ 、 $Q$ 两点第一次相遇时， $t =$ 秒；第 $n$ 次相遇时， $t =$ 秒．

查看试题解析
16. 如图，在四边形ABCD中，AD∥BC，AD=12 cm，BC=15 cm，点P自点A向D以1 cm/s的速度运动，到点D即停止点Q自点C向B以2cm/s的速度运动，到点B即停止，直线PQ截原四边形为两个新四边形．则当P，Q同时出发s时其中一个新四边形为平行四边形．

查看试题解析
17. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $A B = 6$ ， $B C = 8$ ，点 $D$ 在线段 $B C$ 上一动点，以 $A C$ 为对角线的平行四边形 $A D C E$ 中，则 $D E$ 的最小值是．

查看试题解析

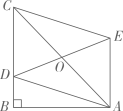
三、解答题

18. 如图，在四边形 $A B C D$ 中， $A B ∥ C D$ ， $∠ A D C = 90 °$ ， $A B = 18 cm$ ， $B C = 13 cm$ ， $C D = 23 cm$ ，动点 $P$ 从点A出发，以 $1 cm/s$ 的速度向终点 $B$ 运动，同时动点 $Q$ 从点 $B$ 出发，以 $2 cm/s$ 的速度沿折线 $B - C - D$ 向终点 $D$ 运动，其中一个动点到达端点时，另一个动点也随之停止运动，设运动时间为 $t$ 秒．

(1)、用含 $t$ 的式子表示 $P B$ ；

(2)、当 $t$ 为何值时，直线 $P Q$ 把四边形 $A B C D$ 分成两个部分，且其中的一部分是平行四边形？

(3)、只改变点 $Q$ 的运动速度，使运动过程中某一时刻四边形 $P B C Q$ 为菱形，则点 $Q$ 的运动速度应为多少？

查看试题解析
19. 如图，□ABCD的对角线 AC，BD 相交于点O，AB⊥AC，BC=5，点 P从点A 出发，沿 AD 以每秒1个单位的速度向终点 D 运动.连结PO并延长，交 BC 于点Q.设点 P 的运动时间为 t秒.

(1)、求 BQ的长(用含 t的代数式表示).

(2)、当四边形 ABQP 是平行四边形时，求t 的值.

查看试题解析
20. 如图，在四边形ABCD中，AD∥BC ， ∠B=90°， $A D = 24 c m$ ， $A B = 8 c m$ ， $B C = 26 c m$ ，动点P从A点开始沿AD边以 $1 c m / s$ 的速度向点D运动，动点Q从C点开始沿CB边以 $3 c m / s$ 的速度向点B运动，P ， Q分别从A ， C同时出发，当其中一个动点到达终点时，另一个动点也随之停止运动．设运动的时间为 $t （ s ）$ ．

(1)、当t为何值时，四边形ABQP是矩形；

(2)、当t为何值时，四边形PQCD是平行四边形？

(3)、问：四边形PQCD是否能成菱形？若能，求出运动时间；若不能，请说明理由.

查看试题解析
21. 如图，在正方形 $A B C D$ 中， $A B = B C = C D = D A = 4$ ， $∠ A = ∠ B = ∠ C = ∠ D = 90 °$ ．动点 $P$ 以每秒1个单位长度的速度从点 $B$ 山发，沿线段 $B C$ 方向运动，动点 $Q$ 同时以每秒4个单位长度的速度从点 $A$ 出发，沿正方形的边 $A D - D C - C B$ 运动，当点 $P$ 与点 $Q$ 相遇时停止运动，设点 $P$ 的运动时间为 $t$ 秒．

(1)、运动时间为秒时，点 $P$ 与点 $Q$ 相遇；

(2)、求 $t$ 为何值时， $△ A B Q$ 是等腰三角形？

(3)、用含 $t$ 的式子表示 $△ A Q P$ 的面积 $S$ ，并写出相应 $t$ 的取值范围；

(4)、连接 $P A$ ，当以点 $Q$ 及正方形的某两个顶点为顶点组成的三角形和 $△ P A B$ 全等时，直接写出 $t$ 的值（点 $P$ 与点 $Q$ 重合时除外）．

查看试题解析
22. 如图，在长方形ABCD中，AB=6cm，AD=2cm，点P以2cm/s的速度从顶点A出发沿折线A→B→C向点C运动，同时点Q以1cm/s的速度从顶点C出发沿边CD向点D运动．当其中一个动点到达末端停止运动时，另一点也停止运动．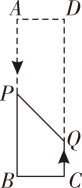

(1)、当四边形PBCQ的面积是长方形ABCD面积的 $\frac{4}{9}$ 时，求出两动点的运动时间t．

(2)、是否存在某一时刻，点P与点Q之间的距离为 $\sqrt{5}$ cm？若存在，则求出运动所需的时间；若不存在，请说明理由．

查看试题解析

四、综合题

23. 如图，在矩形 $A B C D$ 中， $A B = 6$ ， $B C = 11$ ， $P$ 是线段 $A D$ 边上的一动点 $($ 不含端点 $A$ ， $D)$ ，连结 $P C$ ， $E$ 是 $A B$ 上一点．

(1)、已知 $B E = 2$ ，是否存在点 $P$ ，使 $∠ E P C = 90 °$ ？若存在，求 $A P$ 的长；若不存在，请说明理由．

(2)、设 $B E = a$ ，若存在点 $P$ 使 $∠ E P C = 90 °$ ，求 $a$ 的取值范围．

查看试题解析
24. 如图（1），在四边形 $A B C D$ 中， $A D$ $∥$ $B C$ ， $A D = 8 c m$ ， $B C = 12 c m$ ，有动点 $P$ 从 $A$ 点出发，在线段 $A D$ 上以 $1 c m / s$ 的速度向点 $D$ 运动，有动点 $Q$ 同时从 $C$ 点出发，在线段 $C B$ 上以 $2 c m / s$ 的速度向点 $B$ 运动，当其中一点到达时，另一点也随之停止运动．连接 $P Q$ ，若运动时间是 $t$ 秒．

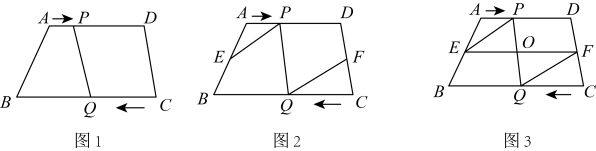(1)、求当四边形 $A B Q P$ 和四边形 $P Q C D$ 其中一个是平行四边形时， $t$ 的取值；

(2)、如图（2），取 $A B$ 中点 $E$ ， $C D$ 中点 $F$ ，连接 $P E$ ， $Q F$ ，请求出使 $P E$ $∥$ $Q F$ 的时间 $t$ ；

(3)、在（2）中，继续连接 $E F$ ，与 $P Q$ 相交与点 $O$ ，如图（3）当 $P E$ $∥$ $Q F$ 时，请写出一个与EF有关的结论，并证明这个结论．

查看试题解析
25. 如图①，在矩形ABCD中，AB=8，AD=4.点P从点A出发，沿A→D→C→D 运动，速度为每秒2个单位长度：点Q从点A出发向点B运动，速度为每秒1个单位长度、P、Q两点同时出发，点Q运动到点B时，两点同时停止运动，设点Q的运动时间为t(秒).连结PQ、AC、CP、CQ.

(1)、点P运动到点C时，t=秒；当点Q运动到终点时，PC的长度为.

(2)、用含t的代数式表示PD的长.

(3)、当三角形CPQ的面积为9时，求t的值.

查看试题解析
26. 在矩形 $A B C D$ 中， $A B = 4 c m ， B C = 8 c m$ ， O为 $A C$ 中点， $A C$ 平分 $∠ E A F$ ， E、F分别在边 $A D$ 、 $B C$ 上，连结 $A F 、 C E 、 E F$ ，且 $E F$ 经过点O.

(1)、如图1，求证四边形 $A F C E$ 为菱形，并求 $A F$ 长；

(2)、如图2，动点P、O分别从A、C两点同时出发，沿 $△ A F B$ 和 $△ C D E$ 各边匀速运动一周.即点P自 $A \to F \to B \to A$ 停止，点Q自 $C \to D \to E \to C$ 停止.在运动过程中，
①已知点P的速度为每秒 $5 c m$ ，点Q的速度为每秒 $4 c m$ ，运动时间为t秒，当A、C、P、Q四点为顶点的四边形是平行四边形时，求t的值.
②若点P、Q的运动路程分别为a、b（单位： $c m$ ， $a b \neq 0$ ），已知A、C、P、Q四点为顶点的四边形是平行四边形，请画出符合题意的图形，并求a与b满足的数量关系式.

查看试题解析
27. 如图，在长方形ABCD中， $A B = 6 c m, B C = 8 c m$ ，动点 $E$ 从点 $A$ 出发，以 $2 c m / s$ 的速度沿 $A \to B \to C$ 的方向向点 $C$ 运动，动点 $F$ 从点 $C$ 出发，以 $1 c m / s$ 的速度向点 $B$ 运动.若 $E$ 、 $F$ 两点同时出发，其中一点运动到终点另一点也停止运动，设运动时间为ts，连结DE、DF.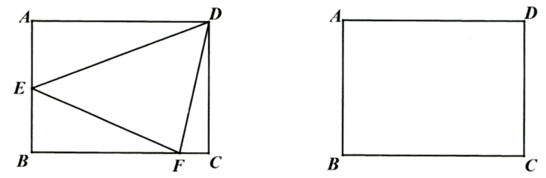

(1)、当t=1时，四边形DEBF的面积等于 $c m^{2}$ .

(2)、当 $t$ 为何值时，线段EF长为 $\sqrt{65} c m$ ?

(3)、当 $t$ 为何值时， $△ D E F$ 的面积为 $9 c m^{2}$ ?

查看试题解析

28. 在某探究课《矩形的折叠》中，每个小组分到了相同大小的矩形纸张

A B C D

，

A B = 10 c m

，

B C = 30 c m

，各小组通过对该纸张的折叠探究了各种不同的折叠问题．

小组	探究内容	图形
第一小组	把 $△ A B C$ 沿 $A C$ 折叠，与 $△ A C D$ 重叠部分记为 $△ A C M$ ．
第二小组	步骤：1：把矩形 $A B C D$ 沿 $E F$ 折叠，使得 $A B$ 与 $D C$ 重合，点E，F分别为 $A D ， B C$ 上的点．步骤2：P为边 $B C$ 上动点（与点B，C不重合）， $△ A P B$ 沿 $A P$ 折叠得到 $△ A P B^{'}$ ．
第三小组	步骤1：把矩形 $A B C D$ 沿 $G H$ 折叠，使得 $A D$ 与 $B C$ 重合，点G，H分别为 $A B ， D C$ 上的点．步骤2：P为边 $B C$ 上动点（与点B，C不重合）， $P B$ 沿过点P的一条折痕折叠得到 $P B^{'}$ ．

根据以上各小组探究内容，求解下列问题．

(1)、根据第一小组探究内容，求证：

△ A C M

是等腰三角形．

(2)、根据第二小组探究内容，当P，

B'

， E三点在同一直线上时，求

B P

的长度．

(3)、根据第三小组探究内容，过点P的折痕使

B^{'}

落在线段

G H

上，请直接写出折痕条数与

B P

长度取值范围的关系．

查看试题解析

五、实践探究题

29. 综合与实践

(1)、【教材情境】
数学活动课上，老师出示了一个问题：如图1，在正方形 $A B C D$ 中，E是BC的中点， $A E ⊥ E P$ ， EP与正方形的外角 $∠ D C G$ 的平分线交于P点．试猜想AE与EP的数量关系，并加以证明；同学们发现，取AB的中点F，连接EF可以解决这个问题，请在图1中补全图形，解答老师提出的问题．

(2)、【实践探究】
“希望小组”受此问题启发，逆向思考这个题目，并提出新的问题：如图2，在正方形 $A B C D$ 中，E为BC边上一动点（点E，B不重合），△AEP是等腰直角三角形， $∠ A E P = 90 °$ ，连接CP，可以求出 $∠ D C P$ 的大小，请你思考并解答这个问题．

(3)、【拓展迁移】
“突击小组”深入研究“希望小组”提出的这个问题，发现并提出新的探究点：如图3，在正方形 $A B C D$ 中，E为BC边上一动点（点E，B不重合），△AEP是等腰直角三角形， $∠ A E P = 90 °$ ，连接DP．知道正方形的边长时，可以求出△ADP周长的最小值．当 $A B = 4$ 时，△ADP周长的最小值为．（直接写出结果）

查看试题解析