2024年浙教版数学八(下)微素养核心突破20图形变换(1):折叠问题
试卷更新日期:2024-06-01 类型:复习试卷
一、矩形的折叠问题
-
1. 如图,将长方形ABCD沿对角线BD折叠,使点C落在点C'处,BC'交AD于E , AD=8,AB=4,则重叠部分(即)的面积为( )
 A、6 B、7.5 C、10 D、202. 如图,把矩形沿翻折,点恰好落在边的处,若 , , 则的面积是( )
A、6 B、7.5 C、10 D、202. 如图,把矩形沿翻折,点恰好落在边的处,若 , , 则的面积是( ) A、 B、 C、 D、3. 如图,在矩形中, , , 将矩形沿折叠,点落在点处,则重叠部分的面积为( )
A、 B、 C、 D、3. 如图,在矩形中, , , 将矩形沿折叠,点落在点处,则重叠部分的面积为( ) A、10 B、12 C、16 D、204. 如图,将矩形沿折叠后点与重合.若原矩形的长宽之比为 , 则的值为( )
A、10 B、12 C、16 D、204. 如图,将矩形沿折叠后点与重合.若原矩形的长宽之比为 , 则的值为( ) A、 B、 C、 D、5. 如图,将矩形ABCD沿对角线AC折叠,点D落在点E处,AE与边BC的交点为M . 已知:AB=1,BC=2,则BM的长等于( )
A、 B、 C、 D、5. 如图,将矩形ABCD沿对角线AC折叠,点D落在点E处,AE与边BC的交点为M . 已知:AB=1,BC=2,则BM的长等于( ) A、 B、 C、 D、6. 如图,在矩形中,为上一点,将矩形的一角沿向上折叠,点的对应点恰好落在边上.若的周长为6,的周长为12,则的长为( )
A、 B、 C、 D、6. 如图,在矩形中,为上一点,将矩形的一角沿向上折叠,点的对应点恰好落在边上.若的周长为6,的周长为12,则的长为( ) A、2 B、 C、 D、17. 如图,矩形ABCD中,AD=5,AB=7.点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D'落在∠ABC的角平分线上时,DE的长为.
A、2 B、 C、 D、17. 如图,矩形ABCD中,AD=5,AB=7.点E为DC上一个动点,把△ADE沿AE折叠,当点D的对应点D'落在∠ABC的角平分线上时,DE的长为. 8. 如图,将长宽比为的矩形沿着折叠,使点C落到宽上点处,点B落到点处,且满足 , 则 .
8. 如图,将长宽比为的矩形沿着折叠,使点C落到宽上点处,点B落到点处,且满足 , 则 . 9. 如图,在矩形中, , , 点P,Q分别为AB,AD上的动点,将沿翻折得到 , 将沿翻折得到在动点P,Q所有位置中,当F,E,P三点共线,时, .
9. 如图,在矩形中, , , 点P,Q分别为AB,AD上的动点,将沿翻折得到 , 将沿翻折得到在动点P,Q所有位置中,当F,E,P三点共线,时, . 10. 如图,矩形纸片ABCD中,是AD上一点,将沿CE对折得到 , 延长CF交AB于点 , 恰有 , 则AE的长为.
10. 如图,矩形纸片ABCD中,是AD上一点,将沿CE对折得到 , 延长CF交AB于点 , 恰有 , 则AE的长为. 11. 如图,将矩形沿折叠,使点D落在点B处,点C落在点处,P为折痕上的任意一点,过点P作 , , 垂足分别为G,H.若 , ,
11. 如图,将矩形沿折叠,使点D落在点B处,点C落在点处,P为折痕上的任意一点,过点P作 , , 垂足分别为G,H.若 , ,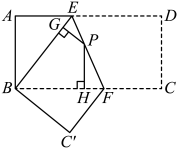
则
(1)、;(2)、则 .12. 如图,在矩形纸片 ABCD中,AB=4,BC=6,将△ABC沿AC 折叠,使点 B 落在点 E 处,CE 交AD 于点 F. (1)、求证:△AEF≌△CDF.(2)、求 DF 的长.13. 如图1,在矩形ABCD中, , 点E,F分别在AD,BC上,将矩形ABCD沿直线EF折叠,使点落在CD边上的处,点落在处,连接.
(1)、求证:△AEF≌△CDF.(2)、求 DF 的长.13. 如图1,在矩形ABCD中, , 点E,F分别在AD,BC上,将矩形ABCD沿直线EF折叠,使点落在CD边上的处,点落在处,连接.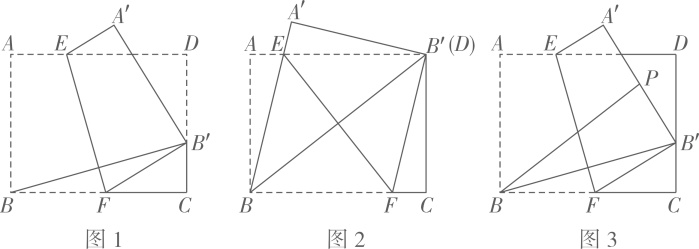 (1)、如图2,若点与点重合,连接EB
(1)、如图2,若点与点重合,连接EB①请你判断四边形的形状,并证明;
②求的长;
(2)、如图3,P为中点,连接BP.①当=2时,求BP的长;
②直接写出BP的取值范围.
14. (1)、【猜想证明】
(1)、【猜想证明】如图1,对折矩形纸片 ABCD,使 AD 与BC 重合,得到折痕 EF,把纸片展平,再次折叠纸片,使点 A 落在 EF 上,并使折痕经过点B,得到折痕 BM,同时得到线段 BN,MN.观察图1,猜想∠MBN的度数是多少,并证明.
(2)、【拓展延伸】在(1)的基础上,再沿 MN 所在的直线折叠,点 B落在AD 上的点B'处,得到折痕MG,同时得到线段 B'G,展开如图2.猜想四边形MBGB'的形状,并证明.
15. [探究与证明]折纸,操作简单,富有数学趣味,我们可以通过折纸开展数学探究,探索数学奥秘.[动手操作]如图①,将矩形纸片ABCD对折,使AD与BC重合,展平纸片,得到折痕EF;折叠纸片,使点B落在EF上,并使折痕经过点A,得到折痕AM,点B,E的对应点分别为B',E',展平纸片,连结AB',BB',BE'.请完成:
 (1)、观察图①中∠1,∠2和∠3,试猜想这三个角的大小关系;(2)、证明(1)中的猜想;(3)、[类比操作]如图②,N为矩形纸片ABCD的边AD上的一点,连接BN,在AB上取一点P,折叠纸片,使B,P两点重合,展平纸片,得到折痕EF ;折叠纸片,使点B,P分别落在EF,BN上,得到折痕l,点B,P的对应点分别为B',P',展平纸片,连接BB',P'B'.请完成:
(1)、观察图①中∠1,∠2和∠3,试猜想这三个角的大小关系;(2)、证明(1)中的猜想;(3)、[类比操作]如图②,N为矩形纸片ABCD的边AD上的一点,连接BN,在AB上取一点P,折叠纸片,使B,P两点重合,展平纸片,得到折痕EF ;折叠纸片,使点B,P分别落在EF,BN上,得到折痕l,点B,P的对应点分别为B',P',展平纸片,连接BB',P'B'.请完成:
求证:BB'是∠NBC的一条三等分线.16. 如图,已知矩形纸片 , , ().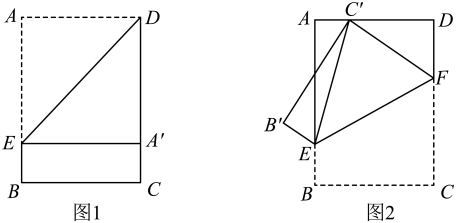 (1)、如图1,将矩形纸片沿过点D的直线折叠,使点A落在边上的点处,折痕交边于点E.求证:四边形是正方形.(2)、将图1中的矩形纸片沿过点E的直线折叠,使点C落在边上的点处,点B落在点处,折痕交边于点F,连结 , 如图2,
(1)、如图1,将矩形纸片沿过点D的直线折叠,使点A落在边上的点处,折痕交边于点E.求证:四边形是正方形.(2)、将图1中的矩形纸片沿过点E的直线折叠,使点C落在边上的点处,点B落在点处,折痕交边于点F,连结 , 如图2,①求证: .
②若 , , 求折痕的长.
③当为等腰三角形时,直接写出a,b之间应满足的数量关系.
二、菱形的折叠问题
-
17. 如图,将菱形沿折叠,点B的对应点为F,若E、F、D刚好在同一直线上,设 , , , 则关系正确的是( )
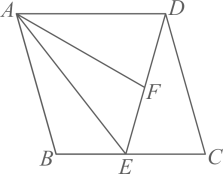 A、 B、 C、 D、18. 如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠BEC'的大小为( )
A、 B、 C、 D、18. 如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠BEC'的大小为( ) A、20° B、25° C、30° D、35°19. 如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:
A、20° B、25° C、30° D、35°19. 如图,菱形ABCD中,∠A是锐角,E为边AD上一点,△ABE沿着BE折叠,使点A的对应点F恰好落在边CD上,连接EF,BF,给出下列结论:①若∠A=70°,则∠ABE=35°;②若点F是CD的中点,则S△ABE S菱形ABCD
下列判断正确的是( )
 A、①,②都对 B、①,②都错 C、①对,②错 D、①错,②对20. 如图,将平行四边形纸片ABCD折叠,使顶点D恰好落在AB边上的点M处,折痕为AN,那么对于结论:①MN∥BC,②MN=AM.下列说法正确的是( )
A、①,②都对 B、①,②都错 C、①对,②错 D、①错,②对20. 如图,将平行四边形纸片ABCD折叠,使顶点D恰好落在AB边上的点M处,折痕为AN,那么对于结论:①MN∥BC,②MN=AM.下列说法正确的是( )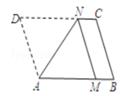 A、①②都错 B、①对②错 C、①错②对 D、①②都对21. 如图,在菱形ABCD中,AB=6,菱形的面积为30;折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD相交于点E,F,当点M的位置变化时,DF的长的最大值为.
A、①②都错 B、①对②错 C、①错②对 D、①②都对21. 如图,在菱形ABCD中,AB=6,菱形的面积为30;折叠该菱形,使点A落在边BC上的点M处,折痕分别与边AB,AD相交于点E,F,当点M的位置变化时,DF的长的最大值为. 22. 如图,菱形中, , M为边上的一点,将菱形沿折叠后,点A恰好落在的中点E处,则 .
22. 如图,菱形中, , M为边上的一点,将菱形沿折叠后,点A恰好落在的中点E处,则 . 23. 如图1,菱形纸片ABCD的边长为6cm,∠ABC=60°,将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上的点P(如图2).若AE=2BE,则六边形AEFCHG的面积为cm2 .
23. 如图1,菱形纸片ABCD的边长为6cm,∠ABC=60°,将菱形ABCD沿EF,GH折叠,使得点B,D两点重合于对角线BD上的点P(如图2).若AE=2BE,则六边形AEFCHG的面积为cm2 .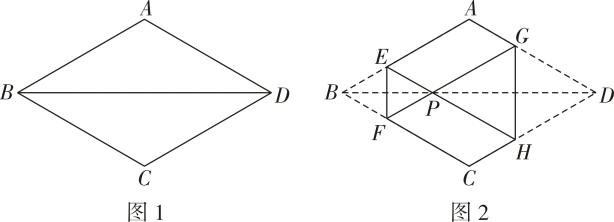 24. 如图,在菱形纸片ABCD中,AB=3,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则EF的长为.
24. 如图,在菱形纸片ABCD中,AB=3,∠A=60°,将菱形纸片翻折,使点A落在CD的中点E处,折痕为FG,点F,G分别在边AB,AD上,则EF的长为. 25. 对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B'两点重合,MN是折痕.若B'M=1,求CN的长.
25. 对角线长分别为6和8的菱形ABCD如图所示,点O为对角线的交点,过点O折叠菱形,使B,B'两点重合,MN是折痕.若B'M=1,求CN的长. 26. 如图,菱形ABCD中,E是AD上的点,沿BE折叠OABE,点A恰好落在BD上的点F处,连结CF,若∠DFC=110°,求∠BAD的度数.
26. 如图,菱形ABCD中,E是AD上的点,沿BE折叠OABE,点A恰好落在BD上的点F处,连结CF,若∠DFC=110°,求∠BAD的度数. 27. 如图矩形OABC的顶点A,C在x,y轴正半轴上,反比例函数y= (x>0)过OB的中点D,与BC,AB交于M,N,且已知D(m,2),N(8,n)
27. 如图矩形OABC的顶点A,C在x,y轴正半轴上,反比例函数y= (x>0)过OB的中点D,与BC,AB交于M,N,且已知D(m,2),N(8,n) (1)、求此反比例函数的解析式;(2)、若将矩形一角折叠,使点O与点M重合,折痕为PQ,求点P的坐标;(3)、如图2,若将△OQM沿OM向左翻折,得到菱形OQMR,将该菱形沿射线OB以每秒 个单位向上平移t秒。
(1)、求此反比例函数的解析式;(2)、若将矩形一角折叠,使点O与点M重合,折痕为PQ,求点P的坐标;(3)、如图2,若将△OQM沿OM向左翻折,得到菱形OQMR,将该菱形沿射线OB以每秒 个单位向上平移t秒。①用t的代数式表示O'和R'的坐标;
②要使该菱形始终与反比例函数图象有交点,求t的取值范围。
28. 已知:如图,将矩形纸片的两个角分别沿 , 向内折起,恰好使点A和点C落在对角线BD上同一点O处. (1)、判断四边形的形状,并说明理由;(2)、若 , 求四边形的面积.29. 将一个直角三角形纸片放置在平面直角坐标系中,已知点 , 点 , 点.P是边上的一动点(点P不与点A、B重合),沿着折叠该纸片,得点A的对应点.
(1)、判断四边形的形状,并说明理由;(2)、若 , 求四边形的面积.29. 将一个直角三角形纸片放置在平面直角坐标系中,已知点 , 点 , 点.P是边上的一动点(点P不与点A、B重合),沿着折叠该纸片,得点A的对应点. (1)、如图1,当点在第一象限,且满足时,求点的坐标;(2)、如图2,当P为中点时,求的长;(3)、当时,直接写出点P的坐标.
(1)、如图1,当点在第一象限,且满足时,求点的坐标;(2)、如图2,当P为中点时,求的长;(3)、当时,直接写出点P的坐标.三、正方形的折叠问题
-
30. 如图,正方形 ABCD的边长为 9,将正方形折叠,使顶点 D落在 BC 边上的点 E 处,折痕为GH.若 BE:EC=2:1,则线段 CH 的长为( )
 A、3 B、4 C、5 D、631. 如图,将正方形按图中虚线折叠可得菱形(分别将正方形各边折叠至对角线 上再展开,折痕所成四边形 即为菱形),已知正方形 的边长为2,则菱形 的面积为( ).
A、3 B、4 C、5 D、631. 如图,将正方形按图中虚线折叠可得菱形(分别将正方形各边折叠至对角线 上再展开,折痕所成四边形 即为菱形),已知正方形 的边长为2,则菱形 的面积为( ). A、 B、 C、 D、32. 如图,已知正方形 的边长为4,点 是正方形 的边 上的一点,把△ABE沿BE翻折到△FBE,若 ,则DF的长为( )
A、 B、 C、 D、32. 如图,已知正方形 的边长为4,点 是正方形 的边 上的一点,把△ABE沿BE翻折到△FBE,若 ,则DF的长为( ) A、2 B、 C、 D、33. 如图,已知正方形ABCD的边长为2,点E是正方形ABCD的边AD上的一点,点A关于BE的对称点为F,若∠DFC=90°,则EF的长为( )
A、2 B、 C、 D、33. 如图,已知正方形ABCD的边长为2,点E是正方形ABCD的边AD上的一点,点A关于BE的对称点为F,若∠DFC=90°,则EF的长为( ) A、 B、 C、 D、34. 如图,在正方形 中,E为边 上一点,将 沿 折叠至 处, 与 交于点F,若 ,则 的大小为( )
A、 B、 C、 D、34. 如图,在正方形 中,E为边 上一点,将 沿 折叠至 处, 与 交于点F,若 ,则 的大小为( )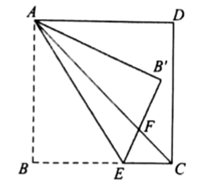 A、 B、 C、 D、35. 甲,乙两位同学采用折叠的方法,判断两张四边形纸片是否为正方形.
A、 B、 C、 D、35. 甲,乙两位同学采用折叠的方法,判断两张四边形纸片是否为正方形.甲:如图①进行两次折叠,每次折叠后折痕两侧部分能完全重合,故判断原四边形是正方形;
乙:如图②进行两次折叠,每次折叠后折痕两侧部分能完全重合,故判断原四边形是正方形.
下列判断正确的是( )
 A、仅甲正确 B、仅乙正确 C、甲、乙均正确 D、甲、乙均错误36. 如图,将边长为 6 cm的正方形纸片 ABCD折叠,使点 D 落在AB边的中点 E 处,点 C 落在点Q处,折痕为 FH,则线段 AF的长为cm.
A、仅甲正确 B、仅乙正确 C、甲、乙均正确 D、甲、乙均错误36. 如图,将边长为 6 cm的正方形纸片 ABCD折叠,使点 D 落在AB边的中点 E 处,点 C 落在点Q处,折痕为 FH,则线段 AF的长为cm. 37. 如图1,已知四边形ABCD是正方形,将△DAE,△DCF分别沿DE,DF向内折叠得到图2,此时DA与DC重合(点A,C都落在点G处).若GF=4,EG=6,则DG的长为.
37. 如图1,已知四边形ABCD是正方形,将△DAE,△DCF分别沿DE,DF向内折叠得到图2,此时DA与DC重合(点A,C都落在点G处).若GF=4,EG=6,则DG的长为. 38. 如图,在正方形中, , 点是的中点,连结 , 则;点F在边AB上,将△BCF沿CF折叠,点B恰好落在CE上的点G处,连结EF,则 .
38. 如图,在正方形中, , 点是的中点,连结 , 则;点F在边AB上,将△BCF沿CF折叠,点B恰好落在CE上的点G处,连结EF,则 . 39. 如图,在正方形ABCD中,点M是AB边上的中点,将正方形ABCD沿DM折叠,使点A落在点E处,延长ME交BC于点N,连结DN.
39. 如图,在正方形ABCD中,点M是AB边上的中点,将正方形ABCD沿DM折叠,使点A落在点E处,延长ME交BC于点N,连结DN. (1)、求证:Rt△CDN≌Rt△EDN;(2)、求∠MDN的度数;(3)、若AB=12,求BN的长.40. 如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A,D重合) ,将正方形纸片沿EF折叠使点B落在点P处,点C落在点G处,PG交DC于点H,连结BP.
(1)、求证:Rt△CDN≌Rt△EDN;(2)、求∠MDN的度数;(3)、若AB=12,求BN的长.40. 如图,有一张边长为6的正方形纸片ABCD,P是AD边上一点(不与点A,D重合) ,将正方形纸片沿EF折叠使点B落在点P处,点C落在点G处,PG交DC于点H,连结BP. (1)、求证:∠APB=∠BPH.(2)、若P为AD中点,求四边形EFGP的面积(3)、当点P在边AD上移动时,△PDH的周长是否发生变化?写出你的结论并证明.41. 如图,在正方形纸片ABCD中,E是CD的中点,将正方形纸片折叠,点B落在线段AE上的点G处,折痕为AF.若AD=4 cm,求CF的长.
(1)、求证:∠APB=∠BPH.(2)、若P为AD中点,求四边形EFGP的面积(3)、当点P在边AD上移动时,△PDH的周长是否发生变化?写出你的结论并证明.41. 如图,在正方形纸片ABCD中,E是CD的中点,将正方形纸片折叠,点B落在线段AE上的点G处,折痕为AF.若AD=4 cm,求CF的长. 42. 如图,边长为2的正方形纸片ABCD中,点M为边CD上一点(不与C,D重合),将△ADM沿AM折叠得到△AME,延长ME交边BC于点N,连结AN.
42. 如图,边长为2的正方形纸片ABCD中,点M为边CD上一点(不与C,D重合),将△ADM沿AM折叠得到△AME,延长ME交边BC于点N,连结AN. (1)、猜想∠MAN的大小是否变化,并说明理由;(2)、如图1,当N点恰为BC中点时,求DM的长度;
(1)、猜想∠MAN的大小是否变化,并说明理由;(2)、如图1,当N点恰为BC中点时,求DM的长度; (3)、如图2,连结BD,分别交AN,AM于点Q,H.若BQ= , 求线段QH的长度.
(3)、如图2,连结BD,分别交AN,AM于点Q,H.若BQ= , 求线段QH的长度.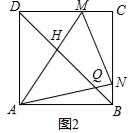 43. 问题情境:数学活动课上,同学们开展了以“矩形纸片折叠”为主题的探究活动(每个小组的矩形纸片规格相同),已知矩形纸片宽 .
43. 问题情境:数学活动课上,同学们开展了以“矩形纸片折叠”为主题的探究活动(每个小组的矩形纸片规格相同),已知矩形纸片宽 .

 (1)、动手实践:如图1,A小组将矩形纸片折叠,点D落在边上的点E处,折痕为 , 连接 , 然后将纸片展平,得到四边形 . 试判断四边形的形状,并加以证明.(2)、如图2,B小组将矩形纸片对折使与重合,展平后得到折痕 , 再次过点A折叠使点D落在折痕上的点N处,得到折痕 , 连结 , 展平后得到四边形 , 请求出四边形的面积.(3)、深度探究:
(1)、动手实践:如图1,A小组将矩形纸片折叠,点D落在边上的点E处,折痕为 , 连接 , 然后将纸片展平,得到四边形 . 试判断四边形的形状,并加以证明.(2)、如图2,B小组将矩形纸片对折使与重合,展平后得到折痕 , 再次过点A折叠使点D落在折痕上的点N处,得到折痕 , 连结 , 展平后得到四边形 , 请求出四边形的面积.(3)、深度探究:
如图 3,C小组将图1中的四边形剪去,然后在边上取点G,H,将四边形沿折叠,使A点的对应点始终落在边上(点不与点D,F重合),点E落在点处,与交于点T.探究①当在上运动时,的周长是否会变化?如变化,请说明理由;如不变,请求出该定值.
探究②直接写出四边形面积的最小值.
44. 如图,在△ABC中,已知∠BAC =45°,AD⊥BC于点 D,BD=2,DC=3,求AD 的长.小萍同学灵活运用轴对称知识,将图形进行翻折变换,巧妙地解答了此题.
请按照小萍同学的思路,探究并解答下列问题:
 (1)、分别以 AB,AC 为对称轴,作出△ABD,△ACD的轴对称图形,点 D 的对称点分别为E,F,延长 EB,FC相交于点G.求证:四边形AEGF 是正方形.(2)、设 AD=x,利用勾股定理,建立关于 x的方程,求出 AD的长.
(1)、分别以 AB,AC 为对称轴,作出△ABD,△ACD的轴对称图形,点 D 的对称点分别为E,F,延长 EB,FC相交于点G.求证:四边形AEGF 是正方形.(2)、设 AD=x,利用勾股定理,建立关于 x的方程,求出 AD的长.