2024年浙教版数学八(下)微素养核心突破19 正方形的十字架模型
试卷更新日期:2024-06-01 类型:复习试卷
一、选择题
-
1. 如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF , AE、BF相交于点O , 下列结论:

(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)中正确的有( )A、4个 B、3个 C、2个 D、1个2. 如图,在正方形ABCD中,点E、F分别在CD、BC上,且BF=CE,连接BE、AF相交于点G,则下列结论不正确的是( ) A、BE=AF B、∠DAF=∠BEC C、∠AFB+∠BEC=90° D、AG⊥BE3. 如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确结论的个数为( )
A、BE=AF B、∠DAF=∠BEC C、∠AFB+∠BEC=90° D、AG⊥BE3. 如图,E、F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论①AE=BF;②AE⊥BF;③AO=OE;④S△AOB=S四边形DEOF中,正确结论的个数为( ) A、4个 B、3个 C、2个 D、1个4. 如图,在正方形ABCD中,点E,F分别在CD,BC上(不与端点重合),且BF=CE,BE与AF相交于点G,则下列结论不正确的是( )
A、4个 B、3个 C、2个 D、1个4. 如图,在正方形ABCD中,点E,F分别在CD,BC上(不与端点重合),且BF=CE,BE与AF相交于点G,则下列结论不正确的是( ) A、BE=AF B、∠DAF=∠BEC C、AG=EG D、AG⊥EG5. 如图,点E、F分别是正方形的边上的点,且相交于点G,下列结论错误的是( )
A、BE=AF B、∠DAF=∠BEC C、AG=EG D、AG⊥EG5. 如图,点E、F分别是正方形的边上的点,且相交于点G,下列结论错误的是( ) A、 B、 C、 D、6. 如图,在正方形ABCD中,点E,F分别是BC,CD上的点,AE与BF相交于点G,连接AC交BF于点H.若CE=DF,BG=GH,AB=2,则△CFH的面积为( )
A、 B、 C、 D、6. 如图,在正方形ABCD中,点E,F分别是BC,CD上的点,AE与BF相交于点G,连接AC交BF于点H.若CE=DF,BG=GH,AB=2,则△CFH的面积为( ) A、3 ﹣4 B、3﹣2 C、 D、7. 如图,在正方形ABCD中,点E,F分别在边AD,CD上,且AE=DF,AF,BE交于点G。若 ,则 的值为( )
A、3 ﹣4 B、3﹣2 C、 D、7. 如图,在正方形ABCD中,点E,F分别在边AD,CD上,且AE=DF,AF,BE交于点G。若 ,则 的值为( ) A、 B、 C、 D、8. 如图,正方形中, , 则 ( )
A、 B、 C、 D、8. 如图,正方形中, , 则 ( ) A、 B、 C、 D、9. 如图,正方形ABCD内有两条相交线段MN,EF,M,N,E,F分别在边AB,CD,AD,BC上.小明认为:若MN=EF,则MN⊥EF;小亮认为:若MN⊥EF,则MN=EF,你认为( )
A、 B、 C、 D、9. 如图,正方形ABCD内有两条相交线段MN,EF,M,N,E,F分别在边AB,CD,AD,BC上.小明认为:若MN=EF,则MN⊥EF;小亮认为:若MN⊥EF,则MN=EF,你认为( ) A、仅小明对 B、仅小亮对 C、两人都对 D、两人都不对
A、仅小明对 B、仅小亮对 C、两人都对 D、两人都不对二、填空题
-
10. 如图,在正方形中,点分别是边上的点,连接 , 若 , 则的度数为 .
 11. 如图,正方形中,平分 , 点在边上,且 , 连接交于点 , 交于点 , 点是线段上的动点,点是线段 上的动点,连接 , , 下列五个结论:①;②;③;④;⑤ , 一定成立的有 . (填序号)
11. 如图,正方形中,平分 , 点在边上,且 , 连接交于点 , 交于点 , 点是线段上的动点,点是线段 上的动点,连接 , , 下列五个结论:①;②;③;④;⑤ , 一定成立的有 . (填序号)
三、解答题
-
12. 如图,在正方形ABCD中,E是BC的中点,连结DE,过点A作AG⊥ED交DE 于点F,交CD于点G.
 (1)、求证:△ADG≌△DCE.(2)、连结 BF.求证:AB=BF.13. 如图,正方形ABCD中,点E , F , H分别是AB , BC , CD的中点,CE , DF交于点G , 连接HG .
(1)、求证:△ADG≌△DCE.(2)、连结 BF.求证:AB=BF.13. 如图,正方形ABCD中,点E , F , H分别是AB , BC , CD的中点,CE , DF交于点G , 连接HG . (1)、求证:△BCE≌△CDF;(2)、若BE=4,求GH的值.14. 如图,在正方形ABCD中,点E,F分别在AD,CD上,且与BE相交于点 .
(1)、求证:△BCE≌△CDF;(2)、若BE=4,求GH的值.14. 如图,在正方形ABCD中,点E,F分别在AD,CD上,且与BE相交于点 . (1)、求证: .(2)、若 , 求AG的长.15.
(1)、求证: .(2)、若 , 求AG的长.15. (1)、如图①,已知正方形ABCD的边长为4,点M和N分别是边BC,CD上两点,且BM=CN,连结AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论.(2)、如图②,已知正方形ABCD的边长为4,点M和N分别从点B,C同时出发,以相同的速度沿BC,CD方向向终点C和D运动,连结AM和BN,交于点P.求△APB周长的最大值.16. 如图,正方形ABCD的对角线AC,BD相交于点O,E是边BC上一点,连结AE交BD于点M,过点B作BF⊥AE于点P,交AC于点G,交CD于点F.
(1)、如图①,已知正方形ABCD的边长为4,点M和N分别是边BC,CD上两点,且BM=CN,连结AM和BN,交于点P.猜想AM与BN的位置关系,并证明你的结论.(2)、如图②,已知正方形ABCD的边长为4,点M和N分别从点B,C同时出发,以相同的速度沿BC,CD方向向终点C和D运动,连结AM和BN,交于点P.求△APB周长的最大值.16. 如图,正方形ABCD的对角线AC,BD相交于点O,E是边BC上一点,连结AE交BD于点M,过点B作BF⊥AE于点P,交AC于点G,交CD于点F. (1)、求证:△ABE≌△BCF.(2)、求证:OM=OG.(3)、若AE平分∠BAC,求证:BM2=2OM2.17. 如图,在正方形ABCD中,点E在边AD上(不与点A,点D重合),连结BE,作 AG⊥BE于点F,交边 CD于点G,连结 CF.
(1)、求证:△ABE≌△BCF.(2)、求证:OM=OG.(3)、若AE平分∠BAC,求证:BM2=2OM2.17. 如图,在正方形ABCD中,点E在边AD上(不与点A,点D重合),连结BE,作 AG⊥BE于点F,交边 CD于点G,连结 CF. (1)、求证:BE=AG.(2)、已知E 是边AD 的中点,AD=10.
(1)、求证:BE=AG.(2)、已知E 是边AD 的中点,AD=10.①分别求AF,BF的长.
②求证:CB=CF.
四、综合题
-
18. 如图 1,在正方形中,点为边上一点,连接 . 点在边上运动.
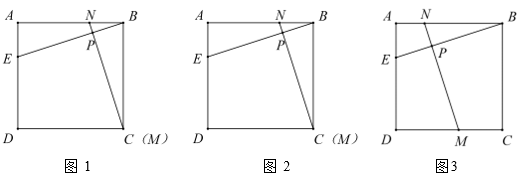
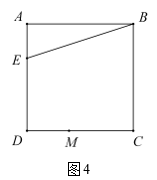 (1)、当点和点重合时(如图2),过点做的垂线,垂足为点 , 交直线于点 . 请直接写出与的数量关系;(2)、当点在边上运动时,过点做的垂线,垂足为点 , 交直线于点(如图 3 ),(1)中的结论依旧成立吗?请证明;(3)、如图 4 ,当点在边上运动时,为直线上一点,若 , 请问是否始终能证明?请你说明理由.19. 问题背景:如图,在正方形中,边长为4.点M,N是边 , 上两点,且 , 连接 , , 与相交于点O.
(1)、当点和点重合时(如图2),过点做的垂线,垂足为点 , 交直线于点 . 请直接写出与的数量关系;(2)、当点在边上运动时,过点做的垂线,垂足为点 , 交直线于点(如图 3 ),(1)中的结论依旧成立吗?请证明;(3)、如图 4 ,当点在边上运动时,为直线上一点,若 , 请问是否始终能证明?请你说明理由.19. 问题背景:如图,在正方形中,边长为4.点M,N是边 , 上两点,且 , 连接 , , 与相交于点O. (1)、探索发现:探索线段与的关系,并说明理由;(2)、探索发现:若点E,F分别是与的中点,计算的长;(3)、拓展提高:延长至P,连接 , 若 , 请直接写出线段的长.
(1)、探索发现:探索线段与的关系,并说明理由;(2)、探索发现:若点E,F分别是与的中点,计算的长;(3)、拓展提高:延长至P,连接 , 若 , 请直接写出线段的长.五、实践探究题
-
20. 如图
 (1)、【问题原型】华师版教材八年级下册第页有这样一道题:
(1)、【问题原型】华师版教材八年级下册第页有这样一道题:如图 , 在正方形中,求证: .
请你完成这一问题的证明过程.(2)、【问题应用】如图,在正方形中, , 、分别是边、上的点,且 .①如图 , 连接、交于点 , 为的中点,连接 , 当为的中点时,四边形的面积为 ;
②如图 , 连接、 , 当点在边上运动时,的最小值为 .
21. 在正方形中,是边上一点点不与点、重合 , 连结 . (1)、【感知】如图 , 过点作交于点易证≌不需要证明(2)、【探究】如图 , 取的中点 , 过点作交于点 , 交于点 .
(1)、【感知】如图 , 过点作交于点易证≌不需要证明(2)、【探究】如图 , 取的中点 , 过点作交于点 , 交于点 .①求证: .
②连结 , 若 , 则的长为 ▲ .
22. 材料:“八年级下册课本第187页例2:四边形是一块正方形的土地,要在这块土地上修建两条笔直的、互相垂直的小路,把这块土地分成面积相等的四部分.你有哪些不同的方案?画出图形,并说明理由.”
小亮在学习了上述解决方案后,发现三种分割方案的图形都是中心对称图形.这对于他创作数学社团图标注入了灵感,经过思考,小亮设计了一个中心对称图形的社团图标,如图所示.已知O为正方形的对称中心,为的直径,连接 , .
(1)、请你说明此图标是中心对称图形;(2)、若 , 则 , , 三者满足 . 请证明.