2024年浙教版数学八(下)微素养核心突破18 正方形与全等模型(2):垂直模型
试卷更新日期:2024-06-01 类型:复习试卷
一、选择题
-
1. 如图,正方形ABCD的边长为 10,AG=CH=8,BG=DH=6,连结GH,则GH 的长为 ( )
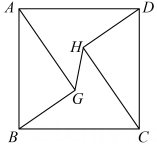 A、 B、2 C、 D、2. 如图,正方形ABCD的对角线AC,BD相交于点O,M是边AD上一点,连结OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A、 B、2 C、 D、2. 如图,正方形ABCD的对角线AC,BD相交于点O,M是边AD上一点,连结OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( ) A、1 B、 C、2 D、23. 如图,在边长为3的正方形ABCD中, , 则BF的长是( )
A、1 B、 C、2 D、23. 如图,在边长为3的正方形ABCD中, , 则BF的长是( ) A、2 B、 C、 D、14. 如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( )
A、2 B、 C、 D、14. 如图,正方形ABCD的对角线AC,BD交于点O,M是边AD上一点,连接OM,过点O作ON⊥OM,交CD于点N.若四边形MOND的面积是1,则AB的长为( ) A、1 B、 C、2 D、5. 如图,四边形ABCD是正方形,BE⊥EF,DF⊥EF,BE=2.5dm,DF=4dm,那么EF的长为( )
A、1 B、 C、2 D、5. 如图,四边形ABCD是正方形,BE⊥EF,DF⊥EF,BE=2.5dm,DF=4dm,那么EF的长为( )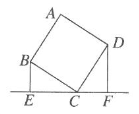 A、6.5dm B、6dm C、5.5dm D、4dm6. 如图,在正方形中,点P在边上,于点E,于点F,若 , , 则( )
A、6.5dm B、6dm C、5.5dm D、4dm6. 如图,在正方形中,点P在边上,于点E,于点F,若 , , 则( ) A、1 B、2 C、3 D、47. 如图,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG于点E,BFDE且交AG于点F,若AB = 4EF,则S正方形ABCD的值为( )
A、1 B、2 C、3 D、47. 如图,四边形ABCD是正方形,G是BC上的任意一点,DE⊥AG于点E,BFDE且交AG于点F,若AB = 4EF,则S正方形ABCD的值为( ) A、9:16 B、17:32 C、17:36 D、18:358. 如图,在中, , 以的各边为边作三个正方形,点落在上,若 , 空白部分面积为 , 则的长为( )
A、9:16 B、17:32 C、17:36 D、18:358. 如图,在中, , 以的各边为边作三个正方形,点落在上,若 , 空白部分面积为 , 则的长为( )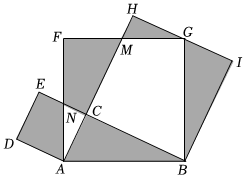 A、 B、 C、 D、9. 如图,边长为的正方形的对角线相交于点O,点G在边上,将正方形沿直线折叠,点C落在对角线上的点E处,折痕交于点M,则的长为( )
A、 B、 C、 D、9. 如图,边长为的正方形的对角线相交于点O,点G在边上,将正方形沿直线折叠,点C落在对角线上的点E处,折痕交于点M,则的长为( )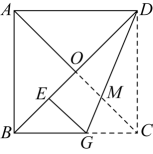 A、 B、 C、 D、10. 如图,在正方形ABCD中,O为对角线AC、BD的交点,E、F分别为边BC、CD上一点,且 , 连接EF . 若∠AOE=150°, , 则EF的长为( )
A、 B、 C、 D、10. 如图,在正方形ABCD中,O为对角线AC、BD的交点,E、F分别为边BC、CD上一点,且 , 连接EF . 若∠AOE=150°, , 则EF的长为( ) A、 B、 C、 D、3
A、 B、 C、 D、3二、填空题
-
11. 如图,正方形ABCD的对角线AC,BD相交于点O,AE平分∠BAC分别交BC,BD于点E,点M,过点B作BF⊥AE于点P,交AC于点G,交CD于点F,则OM与OG存在数量关系;当OM=1时,则BM= .
 12. 如图,小明同学将边长为5cm的正方形塑料模板ABCD与一块足够大的直角三角板叠放在一起,其中直角三角板的直角顶点落在点A处,两条直角边分别与CD交于点F,与CB延长线交于点E,则四边形AECF的面积是 .
12. 如图,小明同学将边长为5cm的正方形塑料模板ABCD与一块足够大的直角三角板叠放在一起,其中直角三角板的直角顶点落在点A处,两条直角边分别与CD交于点F,与CB延长线交于点E,则四边形AECF的面积是 . 13. 如图,直线l正方形ABCD的顶点B,点A、点C到直线l的距离分别是3和4,则该正方形的面积是.
13. 如图,直线l正方形ABCD的顶点B,点A、点C到直线l的距离分别是3和4,则该正方形的面积是.
 14. 如图,边长为2的正方形的对角线相交于点O,点E是边上的动点,连接并延长交的延长线于点P,过点O作交于点F,交延长线于点Q,连接 . 若点恰好是中点时,则 .
14. 如图,边长为2的正方形的对角线相交于点O,点E是边上的动点,连接并延长交的延长线于点P,过点O作交于点F,交延长线于点Q,连接 . 若点恰好是中点时,则 .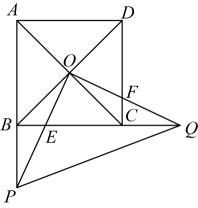 15. 如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,已知正方形边长为4,则EF的长为 .
15. 如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F,已知正方形边长为4,则EF的长为 .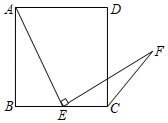 16. 正方形ABCD的边长为2,如图1,点E,F均在正方形内部,且BE=EF=FD,∠E=∠F=90°,则BE的长为;如图2,点G,H,I,J,K,L均在正方形内部,且BG=GH=HI=IJ=JK=KL=LD,∠G=∠H=∠I=∠J=∠K=∠L=90°,则BG的长为.
16. 正方形ABCD的边长为2,如图1,点E,F均在正方形内部,且BE=EF=FD,∠E=∠F=90°,则BE的长为;如图2,点G,H,I,J,K,L均在正方形内部,且BG=GH=HI=IJ=JK=KL=LD,∠G=∠H=∠I=∠J=∠K=∠L=90°,则BG的长为.
三、解答题
-
17.
 (1)、如图①,在正方形ABCD中,E为边CD上一点,连结AE,过点A作AF⊥AE交CB的延长线于点F,猜想AE与AF的数量关系,并说明理由;(2)、如图②,在(1)的条件下,连结AC,过点A作AM⊥AC交CB的延长线于点M ,观察并猜想CE与MF的数量关系,并说明理由.18. 如图①,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形ABCD的外角∠DCG的平分线CF于点F.
(1)、如图①,在正方形ABCD中,E为边CD上一点,连结AE,过点A作AF⊥AE交CB的延长线于点F,猜想AE与AF的数量关系,并说明理由;(2)、如图②,在(1)的条件下,连结AC,过点A作AM⊥AC交CB的延长线于点M ,观察并猜想CE与MF的数量关系,并说明理由.18. 如图①,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形ABCD的外角∠DCG的平分线CF于点F. (1)、如图②,取AB的中点H,连结HE,求证:AE=EF.(2)、如图③,若点E是BC的延长线上(除点C外)的任意一点,其他条件不变,结论“AE=EF"仍然成立吗?如果成立,写出证明过程;如果不成立,请说明理由.19. 如图所示,直线a经过正方形ABCD的顶点A,分别过正方形ABCD的顶点B,D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,求EF的长.
(1)、如图②,取AB的中点H,连结HE,求证:AE=EF.(2)、如图③,若点E是BC的延长线上(除点C外)的任意一点,其他条件不变,结论“AE=EF"仍然成立吗?如果成立,写出证明过程;如果不成立,请说明理由.19. 如图所示,直线a经过正方形ABCD的顶点A,分别过正方形ABCD的顶点B,D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,求EF的长. 20. 如图,四边形ABCD是正方形,C是BC上任意一点,DE⊥AG于点E,BF∥DE,且交AG于点F.求证:DE-BF=EF.
20. 如图,四边形ABCD是正方形,C是BC上任意一点,DE⊥AG于点E,BF∥DE,且交AG于点F.求证:DE-BF=EF. 21. 如图①,在正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与点A,O重合)的一个动点,过点P作PE⊥PB且PE交边CD于点E.
21. 如图①,在正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与点A,O重合)的一个动点,过点P作PE⊥PB且PE交边CD于点E. (1)、求证:PE=PB.(2)、如图②,若正方形ABCD的边长为2,过点E作EF⊥AC于点F,在点P运动的过程中,PF的长度是否发生变化?若不变,试求出这个不变的值;若变化,请说明理由.(3)、用等式表示线段PC,PA,CE之间的数量关系.22. 如图,在正方形ABCD中,点E在边AD上(不与点A,点D重合),连结BE,作 AG⊥BE于点F,交边 CD于点G,连结 CF.
(1)、求证:PE=PB.(2)、如图②,若正方形ABCD的边长为2,过点E作EF⊥AC于点F,在点P运动的过程中,PF的长度是否发生变化?若不变,试求出这个不变的值;若变化,请说明理由.(3)、用等式表示线段PC,PA,CE之间的数量关系.22. 如图,在正方形ABCD中,点E在边AD上(不与点A,点D重合),连结BE,作 AG⊥BE于点F,交边 CD于点G,连结 CF. (1)、求证:BE=AG.(2)、已知E 是边AD 的中点,AD=10.
(1)、求证:BE=AG.(2)、已知E 是边AD 的中点,AD=10.①分别求AF,BF的长.
②求证:CB=CF.
23. (1)、如图1,四边形是正方形,点G是边的中点, , 且交正方形外角的平分线于点F , 求证:.
(1)、如图1,四边形是正方形,点G是边的中点, , 且交正方形外角的平分线于点F , 求证:.小明展示了一种正确的解题思路:取的中点M , 连接 , 请你写出证明过程.
(2)、如图2,如果把“点G是边的中点”改为“点G是边上(除A、B外)的任意一点”,其他条件不变,那么结论“”仍然成立.这个结论正确吗?如果正确,写出证明过程;如果不正确,请说明理由;(3)、若点G在边的延长线上的任意一点,其他条件不变,结论“.”仍然成立,你认为(1)的结论还正确吗?如果正确,写出证明过程;如果不正确,请说明理由.四、综合题
-
24. 如图,在正方形中,E是边上的一点,F是边延长线上的一点,且 .
 (1)、求证:;(2)、求的度数.25. 如图1,在正方形中,点E在上,点F在的延长线上, .
(1)、求证:;(2)、求的度数.25. 如图1,在正方形中,点E在上,点F在的延长线上, . (1)、求证:;(2)、连接 , 若 , 请利用图2验证勾股定理.26. 四边形为正方形,E为对角线上一点,连接 .
(1)、求证:;(2)、连接 , 若 , 请利用图2验证勾股定理.26. 四边形为正方形,E为对角线上一点,连接 .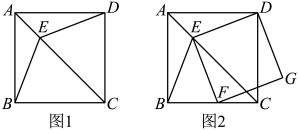 (1)、如图1,求证:;(2)、如图2,过点E作 , 交边于点F,以为邻边作矩形 .
(1)、如图1,求证:;(2)、如图2,过点E作 , 交边于点F,以为邻边作矩形 .①求证:矩形是正方形;
②若正方形的边长为6, , 求正方形的边长.
27. 如图,点E,F分别在正方形ABCD的边CD,BC上,且DE=CF,点P在射线BC上(点P不与点F重合).将线段EP绕点E顺时针旋转90得到线段EG,过点E作GD的垂线QH,垂足为点H,交射线BC于点Q.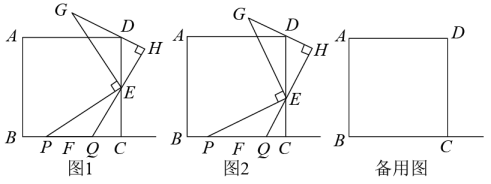 (1)、如图①,若点E是CD的中点,点P在线段BF上,则线段BP,QC,EC的数量关系为;(2)、如图②,若点E不是CD的中点,点P在线段BF上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由;(3)、若正方形ABCD的边长为6,AB=3DE,CQ=1,请直接写出线段BP的长.28. 从反思中总结基本活动经验是一个重要的学习方法.例如,我们在全等学习中所总结的“一线三等角、K型全等”这一基本图形,可以使得我们在观察新问题的时候很自然地联想,借助已有经验,迅速解决问题.(1)、如图1,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,且MN=DM.
(1)、如图①,若点E是CD的中点,点P在线段BF上,则线段BP,QC,EC的数量关系为;(2)、如图②,若点E不是CD的中点,点P在线段BF上,判断(1)中的结论是否仍然成立.若成立,请写出证明过程;若不成立,请说明理由;(3)、若正方形ABCD的边长为6,AB=3DE,CQ=1,请直接写出线段BP的长.28. 从反思中总结基本活动经验是一个重要的学习方法.例如,我们在全等学习中所总结的“一线三等角、K型全等”这一基本图形,可以使得我们在观察新问题的时候很自然地联想,借助已有经验,迅速解决问题.(1)、如图1,在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,且MN=DM.设OM=a,请你利用基本活动经验直接写出点N的坐标(用含a的代数式表示);
 (2)、如果(1)的条件去掉“且MN=DM”,加上“交∠CBE的平分线与点N”,如图2,求证:MD = MN.如何获得问题的解决,不妨在OD上取一点G,连接MG,设法构造△MDG与△NMB全等,请你按此思路证明:MD = MN.
(2)、如果(1)的条件去掉“且MN=DM”,加上“交∠CBE的平分线与点N”,如图2,求证:MD = MN.如何获得问题的解决,不妨在OD上取一点G,连接MG,设法构造△MDG与△NMB全等,请你按此思路证明:MD = MN. (3)、如图3,(2)的条件下请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,请你指出正确的结论,并给出证明.
(3)、如图3,(2)的条件下请你继续探索:连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,请你指出正确的结论,并给出证明.
五、实践探究题
-
29. 综合与实践
 (1)、【教材情境】
(1)、【教材情境】数学活动课上,老师出示了一个问题:如图1,在正方形中,E是BC的中点, , EP与正方形的外角的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;同学们发现,取AB的中点F,连接EF可以解决这个问题,请在图1中补全图形,解答老师提出的问题.
(2)、【实践探究】“希望小组”受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形中,E为BC边上一动点(点E,B不重合),△AEP是等腰直角三角形, , 连接CP,可以求出的大小,请你思考并解答这个问题.
(3)、【拓展迁移】“突击小组”深入研究“希望小组”提出的这个问题,发现并提出新的探究点:如图3,在正方形中,E为BC边上一动点(点E,B不重合),△AEP是等腰直角三角形, , 连接DP.知道正方形的边长时,可以求出△ADP周长的最小值.当时,△ADP周长的最小值为 . (直接写出结果)