2024年浙教版数学八(下)微素养核心突破16 含60°角的菱形
试卷更新日期:2024-06-01 类型:复习试卷
一、选择题
-
1. 如图,已知菱形的周长为 , , 则对角线的长是( )
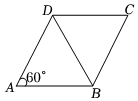 A、 B、 C、 D、2. 根据四边形的不稳定性,当变动∠B的度数时,菱形ABCD的形状会发生改变,当∠B=60°时,如图①所示,AC=;当∠B=90°时,如图②所示,AC等于( )
A、 B、 C、 D、2. 根据四边形的不稳定性,当变动∠B的度数时,菱形ABCD的形状会发生改变,当∠B=60°时,如图①所示,AC=;当∠B=90°时,如图②所示,AC等于( )

① ②
A、 B、2 C、2 D、3. 如图,在菱形ABCD中,∠B=60°,连接AC,若AC=6,则菱形ABCD的周长为( )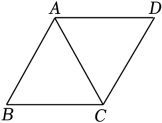 A、24 B、30 C、 D、4. 如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠BEC'的大小为( )
A、24 B、30 C、 D、4. 如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠BEC'的大小为( ) A、20° B、25° C、30° D、35°5. 如图,在菱形ABCD中,∠A=60°,AB=8cm,则菱形ABCD的面积是( )cm2
A、20° B、25° C、30° D、35°5. 如图,在菱形ABCD中,∠A=60°,AB=8cm,则菱形ABCD的面积是( )cm2 A、16 B、32 C、64 D、326. 如图,在菱形ABCD中,E是对角线AC上的一点,过点E作FH AD,GI AB,点F,G,H,I分别在AB,BC,CD,DA上.若AC=a,∠B=60°,则图中阴影部分的周长为( )
A、16 B、32 C、64 D、326. 如图,在菱形ABCD中,E是对角线AC上的一点,过点E作FH AD,GI AB,点F,G,H,I分别在AB,BC,CD,DA上.若AC=a,∠B=60°,则图中阴影部分的周长为( )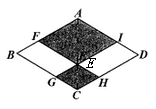 A、 B、4a C、 D、6a7. 如图,在边长为4的菱形中, , 点、分别为、边上的动点,连接、、 . 若 , 则以下结论正确的是( )
A、 B、4a C、 D、6a7. 如图,在边长为4的菱形中, , 点、分别为、边上的动点,连接、、 . 若 , 则以下结论正确的是( )①;②是等边三角形;③四边形的面积是;④面积有最大值为 .
 A、①② B、①②③ C、①②④ D、①②③④8. 如图,有六根长度相同的木条,小明先用四根木条制作了能够活动的菱形学具,他先将该活动学具调成图1所示菱形,测得∠B=60°,对角线AC=10cm,接着将该活动学具调成图2所示正方形,最后用剩下的两根木条搭成了如图3所示的图形,连接BE,则图3中△BCE的面积为( )
A、①② B、①②③ C、①②④ D、①②③④8. 如图,有六根长度相同的木条,小明先用四根木条制作了能够活动的菱形学具,他先将该活动学具调成图1所示菱形,测得∠B=60°,对角线AC=10cm,接着将该活动学具调成图2所示正方形,最后用剩下的两根木条搭成了如图3所示的图形,连接BE,则图3中△BCE的面积为( ) A、 cm2 B、50cm2 C、 cm2 D、25cm29. 如图,AC为边长为2 的菱形ABCD的对角线,∠ABC=60°,点M,N分别从点B,C同时出发,以相同的速度沿BC,CA向终点C和A运动,连接AM和BN,求△APB面积的最大值是( )
A、 cm2 B、50cm2 C、 cm2 D、25cm29. 如图,AC为边长为2 的菱形ABCD的对角线,∠ABC=60°,点M,N分别从点B,C同时出发,以相同的速度沿BC,CA向终点C和A运动,连接AM和BN,求△APB面积的最大值是( ) A、2 B、4+2 C、1+ D、
A、2 B、4+2 C、1+ D、二、填空题
-
10. 如图,菱形ABCD的周长是16,∠ABC=60°,则对角线 AC的长为.
 11. 如图,在菱形ABCD中,∠A=60°,E , F分别是AB , AD的中点,DE , BF相交于点G , 连接BD , CG . 有下列结论:①∠BGD=120°;②BG+DG=CG;③BD=CG;④ . 其中正确的有(将正确答案的序号填在横线上).
11. 如图,在菱形ABCD中,∠A=60°,E , F分别是AB , AD的中点,DE , BF相交于点G , 连接BD , CG . 有下列结论:①∠BGD=120°;②BG+DG=CG;③BD=CG;④ . 其中正确的有(将正确答案的序号填在横线上). 12. 如图,是以菱形的对角线为边的等边三角形,点C与点E关于x轴对称,若点B的坐标是 , 则点E的坐标为 .
12. 如图,是以菱形的对角线为边的等边三角形,点C与点E关于x轴对称,若点B的坐标是 , 则点E的坐标为 . 13. 如图,在边长为5的菱形中, , 点E、点F分别在、上,且 , 连接 , 若 , 则的长度为 .
13. 如图,在边长为5的菱形中, , 点E、点F分别在、上,且 , 连接 , 若 , 则的长度为 . 14. 三个形状、大小相同的菱形按如图的方式摆放,若为正三角形,且边长为6,则一个菱形的面积为.
14. 三个形状、大小相同的菱形按如图的方式摆放,若为正三角形,且边长为6,则一个菱形的面积为. 15. 如图,已知菱形的边长为6,且 , 点分别在边上,将菱形沿折叠,使点B正好落在边上的点G处.若 , 则的长为 .
15. 如图,已知菱形的边长为6,且 , 点分别在边上,将菱形沿折叠,使点B正好落在边上的点G处.若 , 则的长为 .
三、综合题
-
16. 如图,在菱形ABCD中,∠C=60°,O为BD的中点,点E在AD上,点F在AB的延长线上,且∠EOF=120°.求证:AE+BF=AB.
 17. 如图1,在正方形ABCD中,P是BD上的一点,点E在AD的延长线上,且PA=PE , PE交CD于F .
17. 如图1,在正方形ABCD中,P是BD上的一点,点E在AD的延长线上,且PA=PE , PE交CD于F .

图1 图2
(1)、求证:PC=PE;(2)、求∠CPE=;(3)、如图2,把正方形ABCD改为菱形ABCD , 其他条件不变,当∠ABC=120o时,连接CE , 试探究线段AP与线段CE的数量关系,并说明理由.18. 已知菱形 , .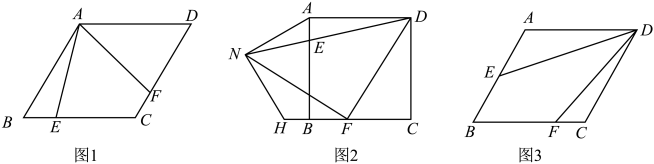 (1)、如图1, , 点E在边上,点F在边上, , 求证:;(2)、如图2, , 点F在边上,点E在边上, , 过点F作交的延长线于点N , 连接 , 过点N作交直线于点H , 求证:点F为的中点;(3)、如图3, , 点E为边的中点,点F在边上, , 直接写出的值 .19. 如图 , 四边形为菱形, . , , .
(1)、如图1, , 点E在边上,点F在边上, , 求证:;(2)、如图2, , 点F在边上,点E在边上, , 过点F作交的延长线于点N , 连接 , 过点N作交直线于点H , 求证:点F为的中点;(3)、如图3, , 点E为边的中点,点F在边上, , 直接写出的值 .19. 如图 , 四边形为菱形, . , , . (1)、点坐标为 ,四边形的面积为 ;(2)、如图 , 点在线段上运动,为等边三角形.
(1)、点坐标为 ,四边形的面积为 ;(2)、如图 , 点在线段上运动,为等边三角形.求证: , 并求的最小值;
点在线段上运动时,点的横坐标是否发生变化?若不变,请求出点的横坐标若变化,请说明理由.
20. 如图,菱形的对角线相交于点O , 过点D作 , 且 , 连接 . (1)、求证:四边形为矩形;(2)、若菱形的边长为4, , 求的长.21. 如图,已知菱形ABCD的边长为6,∠B=60°,点E,F分别是边BC,CD上的动点(不与端点重合),且∠EAF'= 60°.
(1)、求证:四边形为矩形;(2)、若菱形的边长为4, , 求的长.21. 如图,已知菱形ABCD的边长为6,∠B=60°,点E,F分别是边BC,CD上的动点(不与端点重合),且∠EAF'= 60°. (1)、求证:△AEF是等边三角形.(2)、点E,F在运动过程中,四边形AECF的面积是否变化?如果变化,请说明理由;如果不变,请求出面积.(3)、当点E在什么位置时,△ECF的面积最大,并求出此时面积的最大值.22. 如图,菱形的边长为 , , , 分别是边、上的两个动点,且满足 .
(1)、求证:△AEF是等边三角形.(2)、点E,F在运动过程中,四边形AECF的面积是否变化?如果变化,请说明理由;如果不变,请求出面积.(3)、当点E在什么位置时,△ECF的面积最大,并求出此时面积的最大值.22. 如图,菱形的边长为 , , , 分别是边、上的两个动点,且满足 . (1)、求的长;(2)、判断的形状;(3)、设的周长为 , 求的最小值.23. 如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB的中点,连结CE.
(1)、求的长;(2)、判断的形状;(3)、设的周长为 , 求的最小值.23. 如图,在四边形ABCD中,AB∥CD,AC平分∠DAB,AB=2CD,E为AB的中点,连结CE. (1)、求证:四边形AECD为菱形;(2)、若∠D=120°,DC=2,求△ABC的面积24. 如图①,在菱形ABCD中,∠BAD=120°,过点A分别作AE⊥BC于点E,AF⊥CD于点F,且∠EAF= 60°.
(1)、求证:四边形AECD为菱形;(2)、若∠D=120°,DC=2,求△ABC的面积24. 如图①,在菱形ABCD中,∠BAD=120°,过点A分别作AE⊥BC于点E,AF⊥CD于点F,且∠EAF= 60°. (1)、写出BE,CF,AB之间的数量关系;(2)、如图②,当∠EAF绕着点A逆时针旋转到∠EAF的两边与菱形的两边相交,但不垂直时,写出BE,DF,AB三者之间的关系,证明你的结论;(3)、如图③,当∠EAF绕着点A逆时针旋转到∠EAF的两边与菱形的两边BC,CD的延长线相交,但不垂直时,请直接写出BE ,DF ,AB三者之间的关系.25. 如图,菱形中, , E为边上一点,点F在的延长线上, , 作点F关于直线的对称点G , 连接 .
(1)、写出BE,CF,AB之间的数量关系;(2)、如图②,当∠EAF绕着点A逆时针旋转到∠EAF的两边与菱形的两边相交,但不垂直时,写出BE,DF,AB三者之间的关系,证明你的结论;(3)、如图③,当∠EAF绕着点A逆时针旋转到∠EAF的两边与菱形的两边BC,CD的延长线相交,但不垂直时,请直接写出BE ,DF ,AB三者之间的关系.25. 如图,菱形中, , E为边上一点,点F在的延长线上, , 作点F关于直线的对称点G , 连接 . (1)、依题意补全图形,并证明;(2)、用等式表示之间的数量关系,并证明.
(1)、依题意补全图形,并证明;(2)、用等式表示之间的数量关系,并证明.四、实践探究题
-
26. 如图①,的顶点P是正方形两条对角线的交点, , 将绕点P旋转,旋转过程中的两边分别与正方形的边和交于点E和点F(点F与点C,D不重合)
 (1)、如图①,当时,之间满足的数量关系是;(2)、如图②,将图①中的正方形改为的菱形,M是中点,其他条件不变,当时,求证: .(3)、在(2)的条件下,若旋转过程中的边与线段延长线交于点E,其他条件不变,探究在整个运动变化过程中,之间满足的数量关系.27. 综合与实践课上,诸葛小组三位同学对含角的菱形进行了探究.
(1)、如图①,当时,之间满足的数量关系是;(2)、如图②,将图①中的正方形改为的菱形,M是中点,其他条件不变,当时,求证: .(3)、在(2)的条件下,若旋转过程中的边与线段延长线交于点E,其他条件不变,探究在整个运动变化过程中,之间满足的数量关系.27. 综合与实践课上,诸葛小组三位同学对含角的菱形进行了探究.【背景】在菱形中, , 作 , 、分别交边、于点P、Q.
 (1)、【感知】
(1)、【感知】如图1,若点P是边的中点,小南经过探索发现了线段与之间的数量关系,请你写出这个关系式 .
(2)、【探究】如图2,小阳说“点P为上任意一点时,(1)中的结论仍然成立”,你同意吗?请说明理由.
(3)、【应用】小宛取出如图3所示的菱形纸片 , 测得 , , 在边上取一点P,连接 , 在菱形内部作 , 交于点Q,当时,请直接写出线段的长.