2024年浙教版数学八(下)微素养核心突破15 中点四边形
试卷更新日期:2024-06-01 类型:复习试卷
一、选择题
-
1. 顺次连接一个矩形各边中点,所得到的四边形一定是( )A、普通四边形 B、菱形 C、矩形 D、正方形2. 如图,顺次连接四边形ABCD的各边的中点,得到四边形EFGH , 在下列条件中,可使四边形EFGH为矩形的是( )
 A、AB=CD B、AC⊥BD C、AC=BD D、3. 如图,顺次连接四边形ABCD各边中点得四边形EFGH , 要使四边形EFGH为矩形,应添加的条件是( )
A、AB=CD B、AC⊥BD C、AC=BD D、3. 如图,顺次连接四边形ABCD各边中点得四边形EFGH , 要使四边形EFGH为矩形,应添加的条件是( ) A、AB DC B、AC=BD C、AC⊥BD D、AB=DC4. 如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,E,F分别是AB,CD的中点,若AC=BD=2,则EF的长是( )
A、AB DC B、AC=BD C、AC⊥BD D、AB=DC4. 如图,四边形ABCD的对角线AC,BD相交于点O,AC⊥BD,E,F分别是AB,CD的中点,若AC=BD=2,则EF的长是( ) A、2 B、 C、 D、5. 如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,则下列结论一定正确的是( )
A、2 B、 C、 D、5. 如图,在四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点,则下列结论一定正确的是( ) A、四边形EFGH是矩形 B、四边形EFGH的内角和小于四边形ABCD的内角和 C、四边形EFGH的周长等于四边形ABCD的对角线长度之和 D、四边形EFGH的面积等于四边形ABCD的面积的6. 如图,E,F,G,H 分别是四边形ABCD 的边AB,BC,CD,DA 的中点,给出下列说法:
A、四边形EFGH是矩形 B、四边形EFGH的内角和小于四边形ABCD的内角和 C、四边形EFGH的周长等于四边形ABCD的对角线长度之和 D、四边形EFGH的面积等于四边形ABCD的面积的6. 如图,E,F,G,H 分别是四边形ABCD 的边AB,BC,CD,DA 的中点,给出下列说法:
①若AC=BD,则四边形 EFGH 为矩形;
②若 AC⊥BD,则四边形 EFGH 为菱形;
③若四边形 EFGH 是平行四边形,则 AC 与BD 互相平分;
④若 AC 与 BD 互相垂直且相等,则四边形EFGH 是正方形.
其中正确的是 ( )
A、③ B、④ C、①② D、②④7. 如图,在平面直角坐标系中,四边形是矩形,点的坐标为 , 点的坐标为 , 点分别是各边的中点,顺次连接各中点,并连接交于点 , 点为的中点,则的长为( ) A、2 B、2.5 C、1.5 D、38. 如图,矩形ABCD的周长为1,连接矩形ABCD四条边中点得到四边形A1B1C1D1 , 再连接四边形A1B1C1D1四条边中点得到四边形A2B2C2D2 , 如此继续下去…,则四边形A10B10C10D10的周长为( )
A、2 B、2.5 C、1.5 D、38. 如图,矩形ABCD的周长为1,连接矩形ABCD四条边中点得到四边形A1B1C1D1 , 再连接四边形A1B1C1D1四条边中点得到四边形A2B2C2D2 , 如此继续下去…,则四边形A10B10C10D10的周长为( )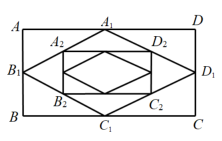 A、()5 B、()10 C、()5 D、()109. 如图,四边形中, , , 且 , 顺次连接四边形各边中点,得到四边形 , 再顺次连接四边形各边中点,得到四边形 , , 如此进行下去,得到四边形下列结论正确的有( )
A、()5 B、()10 C、()5 D、()109. 如图,四边形中, , , 且 , 顺次连接四边形各边中点,得到四边形 , 再顺次连接四边形各边中点,得到四边形 , , 如此进行下去,得到四边形下列结论正确的有( )①四边形是矩形;
②四边形是菱形;
③四边形的周长是;
④四边形的面积是 .
 A、个 B、个 C、个 D、个10. 如图,正方形中,点 , , , 分别是各边的中点,连结 , 取的中点 , 连结 , , 则下列说法正确的是( )
A、个 B、个 C、个 D、个10. 如图,正方形中,点 , , , 分别是各边的中点,连结 , 取的中点 , 连结 , , 则下列说法正确的是( ) A、 B、四边形的周长是周长的倍 C、 D、四边形的面积是面积的倍
A、 B、四边形的周长是周长的倍 C、 D、四边形的面积是面积的倍二、填空题
-
11. 如图,已知第1个矩形的面积为 , 依次连接第1个矩形各边中点得到1个菱形,再依次连接菱形各边中点得到第2个矩形,按此方法继续下去,则第个矩形的面积为 .
 12. 如图,在四边形ABCD中,对角线AC,BD相交于点O,点E、F、G、H分别是AB、BC、CD、AD的中点,顺次连接E、F、G、H.若 , , 则四边形EFGH的面积为 .
12. 如图,在四边形ABCD中,对角线AC,BD相交于点O,点E、F、G、H分别是AB、BC、CD、AD的中点,顺次连接E、F、G、H.若 , , 则四边形EFGH的面积为 .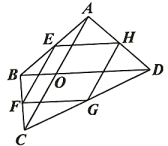 13. 画一个任意四边形 , 顺次连接各边中点E、F、G、H,所得到的新四边形称为中点四边形.当原四边形满足时,中点四边形为菱形.14. 如图,在四边形ABCD中,对角线AC,BD相交于点O,E,F,G,H分别是边AB,BC,CD,DA的中点,只需添加一个条件,即可证明四边形EFCH是矩形,这个条件可以是(写出一个即可).
13. 画一个任意四边形 , 顺次连接各边中点E、F、G、H,所得到的新四边形称为中点四边形.当原四边形满足时,中点四边形为菱形.14. 如图,在四边形ABCD中,对角线AC,BD相交于点O,E,F,G,H分别是边AB,BC,CD,DA的中点,只需添加一个条件,即可证明四边形EFCH是矩形,这个条件可以是(写出一个即可).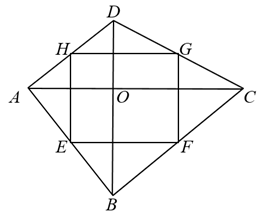 15. 如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的中点,要使四边形EFGH是菱形,四边形ABCD的边AB、CD应满足的条件是.
15. 如图,在四边形ABCD中,E,F,G,H分别是BC,AC,AD,BD的中点,要使四边形EFGH是菱形,四边形ABCD的边AB、CD应满足的条件是.
三、解答题
-
16. 如图,点E、F、G、H分别为矩形ABCD四条边的中点,证明:四边形EFGH是菱形.
 17. 如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH,当四边形ABCD的对角线满足什么条件时,四边形EFGH是矩形,并说明理由.
17. 如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH,当四边形ABCD的对角线满足什么条件时,四边形EFGH是矩形,并说明理由.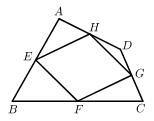 18. 如图,在四边形ABCD中,E,F,G,H分别是AD,BD,BC,AC上的中点,AB=5,CD=7.求四边形EFGH的周长.
18. 如图,在四边形ABCD中,E,F,G,H分别是AD,BD,BC,AC上的中点,AB=5,CD=7.求四边形EFGH的周长.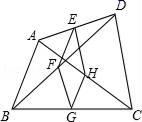
四、综合题
-
19. 四边形 , 点分别是边的中点.
 (1)、如图1,顺次连结得到四边形 , 试猜想四边形的形状并证明;(2)、如图2,若 , 顺次连结得到四边形 , 试猜想四边形的形状并证明.20. 如图1所示:在中,点D、E分别是的中点,
(1)、如图1,顺次连结得到四边形 , 试猜想四边形的形状并证明;(2)、如图2,若 , 顺次连结得到四边形 , 试猜想四边形的形状并证明.20. 如图1所示:在中,点D、E分别是的中点, (1)、直接写出与的之间的关系: .(2)、如图2,点D、E、F分别是三边中点,图中有个平行四边形;(3)、如图3,点P、Q、R、S分别是四边形的中点,问图中是否有平行四边形,请指出并证明你所指出的四边形是平行四边形.21. 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
(1)、直接写出与的之间的关系: .(2)、如图2,点D、E、F分别是三边中点,图中有个平行四边形;(3)、如图3,点P、Q、R、S分别是四边形的中点,问图中是否有平行四边形,请指出并证明你所指出的四边形是平行四边形.21. 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形). (1)、四边形EFGH的形状是 .(2)、证明你的结论.(3)、当满足时,四边形是菱形.(4)、当满足时,四边形是矩形.(5)、当满足时,四边形是正方形.22. 如图①,△ABC中,AB=AC,点M、N分别是AB、AC上的点,且AM=AN.连接MN、CM、BN,点D、E、F、G分别是BC、MN、BN、CM的中点,连接E、F、D、G.
(1)、四边形EFGH的形状是 .(2)、证明你的结论.(3)、当满足时,四边形是菱形.(4)、当满足时,四边形是矩形.(5)、当满足时,四边形是正方形.22. 如图①,△ABC中,AB=AC,点M、N分别是AB、AC上的点,且AM=AN.连接MN、CM、BN,点D、E、F、G分别是BC、MN、BN、CM的中点,连接E、F、D、G. (1)、判断四边形EFDG的形状是(不必证明);(2)、现将△AMN绕点A旋转一定的角度,其他条件不变(如图②),四边形EFDG的形状是否发生变化?证明你的结论;(3)、如图②,在(2)的情况下,请将△ABC在原有的条件下添加一个条件,使四边形EFDG是正方形.请写出你添加的条件,并在添加条件的基础上证明四边形EFDG是正方形.23. 阅读理解:我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形.如图1,在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,依次连接各边中点得到中点四边形EFGH.
(1)、判断四边形EFDG的形状是(不必证明);(2)、现将△AMN绕点A旋转一定的角度,其他条件不变(如图②),四边形EFDG的形状是否发生变化?证明你的结论;(3)、如图②,在(2)的情况下,请将△ABC在原有的条件下添加一个条件,使四边形EFDG是正方形.请写出你添加的条件,并在添加条件的基础上证明四边形EFDG是正方形.23. 阅读理解:我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形.如图1,在四边形ABCD中,E、F、G、H分别是边AB、BC、CD、DA的中点,依次连接各边中点得到中点四边形EFGH. (1)、判断图1中的中点四边形EFGH的形状,并说明理由;(2)、当图1中的四边形ABCD的对角线添加条件时,这个中点四边形EFGH是矩形;四边形ABCD的对角线添加条件时,这个中点四边形EFGH是菱形.(3)、如图2,在四边形ABCD中,点M在AB上且△AMD和△MCB为等边三角形,E、F、G、H分别为AB、BC、CD、AD的中点,试判断四边形EFGH的形状,并证明你的结论.24. 如图1,是线段上的一点,在的同侧作和 , 使 , , , 连接 , 点 , , , 分别是 , , , 的中点,顺次连接 , , , .
(1)、判断图1中的中点四边形EFGH的形状,并说明理由;(2)、当图1中的四边形ABCD的对角线添加条件时,这个中点四边形EFGH是矩形;四边形ABCD的对角线添加条件时,这个中点四边形EFGH是菱形.(3)、如图2,在四边形ABCD中,点M在AB上且△AMD和△MCB为等边三角形,E、F、G、H分别为AB、BC、CD、AD的中点,试判断四边形EFGH的形状,并证明你的结论.24. 如图1,是线段上的一点,在的同侧作和 , 使 , , , 连接 , 点 , , , 分别是 , , , 的中点,顺次连接 , , , .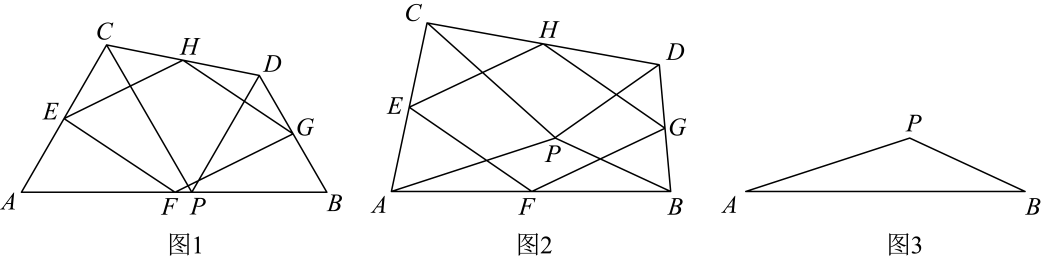 (1)、猜想四边形的形状,直接回答,不必说明理由;(2)、点在线段的上方时,如图2,在的外部作和 , 其他条件不变,(1)中的结论还成立吗?说明理由;(3)、如果(2)中, , 其他条件不变,先补全图3,再判断四边形的形状,并说明理由.
(1)、猜想四边形的形状,直接回答,不必说明理由;(2)、点在线段的上方时,如图2,在的外部作和 , 其他条件不变,(1)中的结论还成立吗?说明理由;(3)、如果(2)中, , 其他条件不变,先补全图3,再判断四边形的形状,并说明理由.