2024年浙教版数学八(下)微素养核心突破14 构造斜边上的中线
试卷更新日期:2024-06-01 类型:复习试卷
一、选择题
-
1. 如图是一张长方形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连接DF、EF,若MF=CD,则∠DAF的度数为( )
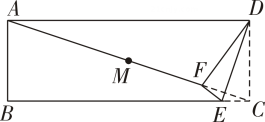 A、15° B、16° C、18° D、20°2. 如图,在矩形纸片中, , 将其折叠,使点与点重合,折痕为 , 设与交于点 , 连接 . 若 , 则的长为( )
A、15° B、16° C、18° D、20°2. 如图,在矩形纸片中, , 将其折叠,使点与点重合,折痕为 , 设与交于点 , 连接 . 若 , 则的长为( )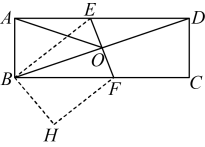 A、 B、 C、 D、3. 如图, , 矩形在的内部,顶点 , 分别在射线 , 上, , , 则点到点的最大距离是( )
A、 B、 C、 D、3. 如图, , 矩形在的内部,顶点 , 分别在射线 , 上, , , 则点到点的最大距离是( ) A、 B、 C、 D、4. 如图,点 是 的边 上一动点,过点 分别作 , 垂足为 , ,连接 ,已知 , , ,当点 运动到 中点时, 等于( )
A、 B、 C、 D、4. 如图,点 是 的边 上一动点,过点 分别作 , 垂足为 , ,连接 ,已知 , , ,当点 运动到 中点时, 等于( )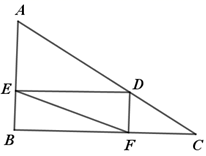 A、6 B、8 C、10 D、145. 如图,某数学兴趣小组开展以下折纸活动:①对折矩形纸片ABCD , 使AD和BC重合,得到折痕EF , 把纸片展开;②再一次折叠纸片,使点A落在EF上,并使折痕经过点B , 得到折痕BM , 同时得到线段BN . 观察探究可以得到∠NBC的度数是( )
A、6 B、8 C、10 D、145. 如图,某数学兴趣小组开展以下折纸活动:①对折矩形纸片ABCD , 使AD和BC重合,得到折痕EF , 把纸片展开;②再一次折叠纸片,使点A落在EF上,并使折痕经过点B , 得到折痕BM , 同时得到线段BN . 观察探究可以得到∠NBC的度数是( ) A、20° B、25° C、30° D、35°6. 如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG﹥60⁰,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )
A、20° B、25° C、30° D、35°6. 如图,已知矩形纸片ABCD,点E是AB的中点,点G是BC上的一点,∠BEG﹥60⁰,现沿直线EG将纸片折叠,使点B落在纸片上的点H处,连接AH,则与∠BEG相等的角的个数为( )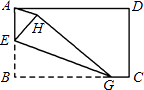
A、4个 B、3个 C、2个 D、1个7. 如图,正方形和正方形中,点在上,已知 , , 点是的中点,则的长是( ) A、 B、3.5 C、4 D、58. 如图,矩形 中, , 分别是边 , 的中点, 于 , 的延长线交 于 .下列结论:① ;② ;③ ;④ .其中结论正确的有( )
A、 B、3.5 C、4 D、58. 如图,矩形 中, , 分别是边 , 的中点, 于 , 的延长线交 于 .下列结论:① ;② ;③ ;④ .其中结论正确的有( )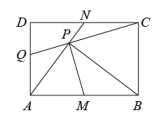 A、1个 B、2个 C、3个 D、4个9. 如图, ,矩形 在 的内部,顶点 , 分别在射线 , 上, , ,则点 到点 的最大距离是( )
A、1个 B、2个 C、3个 D、4个9. 如图, ,矩形 在 的内部,顶点 , 分别在射线 , 上, , ,则点 到点 的最大距离是( ) A、 B、 C、 D、10. 如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )
A、 B、 C、 D、10. 如图,在矩形ABCD中,AB=6,AD=8,以BC为斜边在矩形的外部作直角三角形BEC,点F是CD的中点,则EF的最大值为( )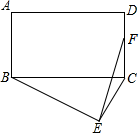 A、8 B、9 C、10 D、2
A、8 B、9 C、10 D、2二、填空题
-
11. 如图,在Rt中,为边BC上一个动点不与B、C重合),PE⊥AB于于F,M为EF中点,则AM的最小值是.
 12. 如图,在正方形中, , 延长到点 , 使得 , , .分别连接 , , 为的中点,则的长为.
12. 如图,在正方形中, , 延长到点 , 使得 , , .分别连接 , , 为的中点,则的长为. 13. 如图,在矩形ABCD中,将矩形ABCD沿EF折叠,点A落在点A'处,点B落在CD边点B'处,连结BB'交EF于点G,点M在A' B'上,A'M=2B'M,若CD=3,AD=6,在折叠的过程中,点B'在边CD上不同的位置时,则MG+ B'G的最小值
13. 如图,在矩形ABCD中,将矩形ABCD沿EF折叠,点A落在点A'处,点B落在CD边点B'处,连结BB'交EF于点G,点M在A' B'上,A'M=2B'M,若CD=3,AD=6,在折叠的过程中,点B'在边CD上不同的位置时,则MG+ B'G的最小值
三、解答题
-
14. 如图,在矩形中,E、F分别是边上的点, , 连接 , 与对角线交于点O,且 , . 若 , 求的长.
 15. 在矩形ABCD中,AB=2,BC=6,点E、F在线段AD上,且∠EBC+∠FCB=90°,求四边形BEFC面积的最大值。
15. 在矩形ABCD中,AB=2,BC=6,点E、F在线段AD上,且∠EBC+∠FCB=90°,求四边形BEFC面积的最大值。 16. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连结DF,EF.若MF=AB,求∠DAF的度数.
16. 如图是一张矩形纸片ABCD,点M是对角线AC的中点,点E在BC边上,把△DCE沿直线DE折叠,使点C落在对角线AC上的点F处,连结DF,EF.若MF=AB,求∠DAF的度数.
四、综合题
-
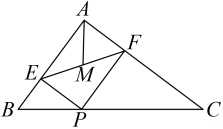
17.(1)、猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,试猜想DM与ME的数量关系,并证明你的结论.
 ①
①
(2)、若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为;(3)、如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,试证明(1)中的结论仍然成立.[提示:直角三角形斜边上的中线等于斜边的一半]
 ② 18. 如图,在矩形ABCD中,AB=3,BC=4,M,N在对角线AC上,且AM=CN,E,F分别是AD, BC的中点
② 18. 如图,在矩形ABCD中,AB=3,BC=4,M,N在对角线AC上,且AM=CN,E,F分别是AD, BC的中点 (1)、求证:△ABM≌△CDN;(2)、点G是对角线AC上的点,∠EGF=90° ,求AG的长.19. 如图1,在平面直角坐标系中,矩形的顶点 , 分别在y轴,x轴上,当在x轴上运动时,A随之在y轴上运动,矩形的形状保持不变,其中 , .
(1)、求证:△ABM≌△CDN;(2)、点G是对角线AC上的点,∠EGF=90° ,求AG的长.19. 如图1,在平面直角坐标系中,矩形的顶点 , 分别在y轴,x轴上,当在x轴上运动时,A随之在y轴上运动,矩形的形状保持不变,其中 , .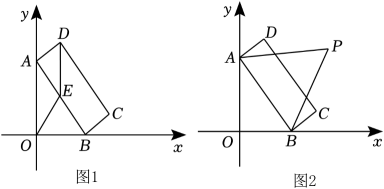 (1)、取的中点 , 连接 , , 求的值.(2)、如图2,若以为边长在第一象限内作等边三角形 , 运动过程中,点到原点的最大距离是多少?20. 请阅读下列材料,并完成相应的任务.
(1)、取的中点 , 连接 , , 求的值.(2)、如图2,若以为边长在第一象限内作等边三角形 , 运动过程中,点到原点的最大距离是多少?20. 请阅读下列材料,并完成相应的任务.三等分角是古希腊三大几何问题之一.如图(1),任意∠ABC可被看作是矩形BCAD的对角线BA与边BC的夹角,以B为端点的射线BF交CA于点 , 交DA的延长线于点F.若 , 则射线BF是∠ABC的一条三等分线.
证明:如图(2),取EF的中点G,连接AG,∵四边形BCAD是矩形,∴ , ADBC.在Rt△AEF中,点G是EF的中点,∴……
 (1)、任务一:上面证明过程中得出“”的依据是;(2)、任务二:完成材料证明中的剩余部分;(3)、任务三:如图(3),在矩形ABCD中,对角线AC的延长线与∠CBE的平分线交于点F,若 , , 请直接写出BF的长.21. 如图,点E是矩形ABCD的边CD上一点,
(1)、任务一:上面证明过程中得出“”的依据是;(2)、任务二:完成材料证明中的剩余部分;(3)、任务三:如图(3),在矩形ABCD中,对角线AC的延长线与∠CBE的平分线交于点F,若 , , 请直接写出BF的长.21. 如图,点E是矩形ABCD的边CD上一点, (1)、如图1,将△ADE沿AE翻折,使点D的对应点M恰好落在BC的中点处,AD=4,求AB的值;(2)、如图2,若点E为CD的中点,过点A作AF⊥BE于F,连接DF,求证:DF=BC.22. 猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,
(1)、如图1,将△ADE沿AE翻折,使点D的对应点M恰好落在BC的中点处,AD=4,求AB的值;(2)、如图2,若点E为CD的中点,过点A作AF⊥BE于F,连接DF,求证:DF=BC.22. 猜想与证明:如图①摆放矩形纸片ABCD与矩形纸片ECGF,使B,C,G三点在一条直线上,CE在边CD上.连结AF,若M为AF的中点,连结DM,ME,
 (1)、试猜想DM与ME的数量关系,并证明你的结论.(2)、拓展与延伸:
(1)、试猜想DM与ME的数量关系,并证明你的结论.(2)、拓展与延伸:①若将“猜想与证明”中的纸片换成正方形纸片ABCD与正方形纸片ECGF,其他条件不变,则DM和ME的关系为;
②如图②摆放正方形纸片ABCD与正方形纸片ECGF,使点F在边CD上,点M仍为AF的中点,猜想并证明DM和ME的关系.下面给出部分证明过程,请把推理过程补充完整.
证明: 如图③,连结AC.
∵四边形ABCD、四边形ECGF都是正方形,
∴∠DAC=∠DCA=∠DCE=∠CFE=45°,
∴点E在AC上.
∴∠AEF=∠FEC=90°.
又∵点M是AF的中点,
∴ME= AF.
23. 如图,在矩形中, , , 点从点出发沿以的速度向点移动;同时,点从点出发沿以的速度向点移动,当其中一点到达终点运动即停止.设运动时间为秒. (1)、在运动过程中,的长度能否为?若能,求出的值,若不能,请说明理由;(2)、在运动过程中,的面积能否为?若能,求出的值,若不能,请说明理由;(3)、取的中点 , 运动过程中,当时,求的值;
(1)、在运动过程中,的长度能否为?若能,求出的值,若不能,请说明理由;(2)、在运动过程中,的面积能否为?若能,求出的值,若不能,请说明理由;(3)、取的中点 , 运动过程中,当时,求的值;五、实践探究题
-
24. 在正方形中,是边上一点点不与点、重合 , 连结 .
 (1)、【感知】如图 , 过点作交于点易证≌不需要证明(2)、【探究】如图 , 取的中点 , 过点作交于点 , 交于点 .
(1)、【感知】如图 , 过点作交于点易证≌不需要证明(2)、【探究】如图 , 取的中点 , 过点作交于点 , 交于点 .①求证: .
②连结 , 若 , 则的长为 ▲ .
25. 阅读下列材料,完成相应任务.直角三角形斜边上的中线等于斜边的一半
如图1, 中, , 是斜边 上的中线.求证: .
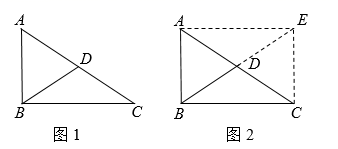
分析:要证明 等于 的一半.可以用“倍长法”将 延长一倍,如图2,延长 到 ,使得 .连接 , .可证四边形 是矩形,由矩形的对角线相等得 ,这样将直角三角形斜边上的中线与斜边的数量关系转化为矩形对角线的数量关系,进而得到 .
 (1)、请你按材料中的分析写出证明过程;(2)、上述证明方法中主要体现的数学思想是______;A、转化思想 B、类比思想 C、数形结合思想 D、从一般到特殊思想(3)、如图3,点 是线段 上一点, ,点 是线段 上一点,分别连接 , ,点 , 分别是 和 的中点,连接 .若 , , .则 .
(1)、请你按材料中的分析写出证明过程;(2)、上述证明方法中主要体现的数学思想是______;A、转化思想 B、类比思想 C、数形结合思想 D、从一般到特殊思想(3)、如图3,点 是线段 上一点, ,点 是线段 上一点,分别连接 , ,点 , 分别是 和 的中点,连接 .若 , , .则 .