2024年浙教版数学八年级下学期期末模拟测试卷
试卷更新日期:2024-06-01 类型:期末考试
一、选择题(每题3分,共30分)
-
1. 下列各式是最简二次根式的是( )A、 B、 C、 D、2. 下列方程中,一定是关于的一元二次方程的是( )A、 B、 C、 D、3. 如图,EF过平行四边形ABCD对角线的交点O,交AD于点E,交BC于点F,若平行四边形ABCD的周长为36,OE=3,则四边形EFCD的周长为( )
 A、28 B、26 C、24 D、204. 若二次根式 有意义,则x的取值范围是( ).A、x> B、x≥ C、x≤ D、x≤55. 如图,四边形是菱形,过点的直线分别交 , 的延长线于点 , , 若 , , 则等于( )
A、28 B、26 C、24 D、204. 若二次根式 有意义,则x的取值范围是( ).A、x> B、x≥ C、x≤ D、x≤55. 如图,四边形是菱形,过点的直线分别交 , 的延长线于点 , , 若 , , 则等于( )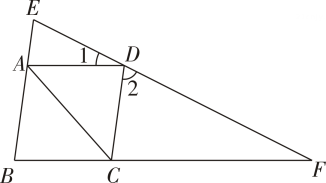 A、 B、 C、 D、6. 已知和是关于x的函数,当时,函数值分别是和 , 若存在实数a , 使得 , 则称函数和是“奇妙函数”.以下函数和不是“奇妙函数”的是( )A、和 B、和 C、和 D、和7. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助此分割方法所得图形证明了勾股定理.如图所示,矩形就是由两个这样的图形拼成(无重叠、无缝隙).下面给出的条件中,一定能求出矩形面积的是( )
A、 B、 C、 D、6. 已知和是关于x的函数,当时,函数值分别是和 , 若存在实数a , 使得 , 则称函数和是“奇妙函数”.以下函数和不是“奇妙函数”的是( )A、和 B、和 C、和 D、和7. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的直角三角形,得到一个恒等式,后人借助此分割方法所得图形证明了勾股定理.如图所示,矩形就是由两个这样的图形拼成(无重叠、无缝隙).下面给出的条件中,一定能求出矩形面积的是( ) A、与的积 B、与的积 C、与的积 D、与的积8. 如图,的斜边OB落在x轴上, , , 以O为圆心.OB长为半径作弧交OC的延长线于点D , 过点C作 , 交圆弧于点E . 若反比例函数的图像经过点E , 则k的值是( )
A、与的积 B、与的积 C、与的积 D、与的积8. 如图,的斜边OB落在x轴上, , , 以O为圆心.OB长为半径作弧交OC的延长线于点D , 过点C作 , 交圆弧于点E . 若反比例函数的图像经过点E , 则k的值是( )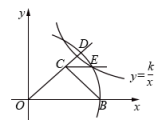 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
9. 使函数有意义的的取值范围是 .10. 为了铸牢学生的安全意识,学校举行了“防溺水”安全知识竞赛,记分员小红将7位评委给某位选手的评分进行整理,并制作成如下表格,若去掉一个最高分和一个最低分后,表中数据一定不发生变化的统计量是 .
平均数
中位数
众数
方差
8.9
9.1
9.1
0.11
11. 一个多边形的内角和是 , 则这个多边形的边数是.12. 把图1中的菱形沿对角线分成四个全等的直角三角形,将这四个直角三角形分别拼成如图2,图3所示的正方形,则图1中菱形的面积为 .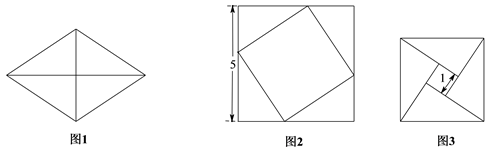 13. 如图,将长 , 宽的矩形纸片ABCD折叠,使点A与C重合,则DF的长为 .
13. 如图,将长 , 宽的矩形纸片ABCD折叠,使点A与C重合,则DF的长为 .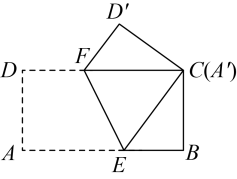 14. 如图,将一副三角尺中,含角的三角尺()的长直角边与含角的三角尺()的斜边重合, , 分别是边 , 上的两点,与交于 , 且四边形是面积为的平行四边形,则线段的长为 .
14. 如图,将一副三角尺中,含角的三角尺()的长直角边与含角的三角尺()的斜边重合, , 分别是边 , 上的两点,与交于 , 且四边形是面积为的平行四边形,则线段的长为 .
三、解答题(共8题,共72分)
-
15. (1)计算:;
(2)解方程:
16. 如图,方格纸中有三个点 A,B,C,按要求作一个四边形,且使这三个点在这个四边形的边(包括顶点)上,四边形的顶点在格点上.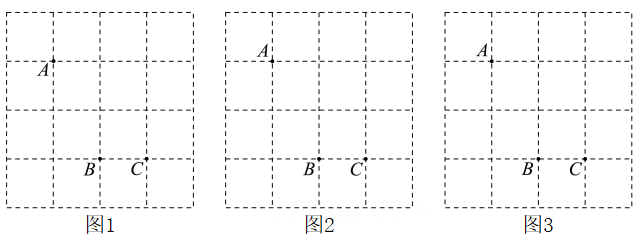 (1)、在图1中作出的四边形要是中心对称图形但不是轴对称图形.(2)、在图2中作出的四边形要是轴对称图形但不是中心对称图形.(3)、在图3中作出的四边形要既是轴对称图形又是中心对称图形.17. 如图,平行四边形的对角线、相交于点 , 点、、、分别是、、、的中点,求证:四边形是平行四边形.
(1)、在图1中作出的四边形要是中心对称图形但不是轴对称图形.(2)、在图2中作出的四边形要是轴对称图形但不是中心对称图形.(3)、在图3中作出的四边形要既是轴对称图形又是中心对称图形.17. 如图,平行四边形的对角线、相交于点 , 点、、、分别是、、、的中点,求证:四边形是平行四边形. 18. 已知反比例函数(k是常数,)与一次函数图象有一个交点的横坐标是 .(1)、求k的值;(2)、求另一个交点坐标;(3)、直接写出时x的取值范围.19. 如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:.
18. 已知反比例函数(k是常数,)与一次函数图象有一个交点的横坐标是 .(1)、求k的值;(2)、求另一个交点坐标;(3)、直接写出时x的取值范围.19. 如图,已知四边形ABCD是正方形,G为线段AD上任意一点,于点E,于点F.求证:. 20. 综合与实践课上,老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动.
20. 综合与实践课上,老师带领同学们以“矩形和平行四边形的折叠”为主题开展数学活动. (1)、操作判断:
(1)、操作判断:如图1,在矩形中,点为边的中点,沿折叠,使点落在点处,把纸片展平,延长与交于点 . 请写出线段与线段的数量关系,并说明理由.
(2)、迁移思考:如图1,若 , 按照(1)中的操作进行折叠和作图,当时,求的值.
(3)、拓展探索:如图2,四边形为平行四边形,其中与是对角,点为边的中点,沿折叠,使点落在点处,把纸片展平,延长与射线交于点 . 若 , , 请直接写出线段的值.
21. 如图1,在中,点E为AD中点,BA , CE延长线交于点F . (1)、求证: .(2)、若时,记AB与CD之间的距离为 , AD与BC之间的距离为 , 求的值.(3)、如图2,连结AC , BD , 在(2)的条件下,求证: .
(1)、求证: .(2)、若时,记AB与CD之间的距离为 , AD与BC之间的距离为 , 求的值.(3)、如图2,连结AC , BD , 在(2)的条件下,求证: .