贵州省2023-2024学年七年级下学期数学期末考试仿真试卷(三)
试卷更新日期:2024-06-01 类型:期末考试
一、选择题
-
1. 在平面直角坐标系中,点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 下列调查中, 最适合用普查方式的是( )
A、调查运动员是否使用兴奋剂的情况
B、考查人们保护环境的意识
C、一批手机的使用寿命情况调查
D、调查某市初中学生对杭州亚运会体育项目知晓情况3. 不等式 的解集在数轴上表示为( )A、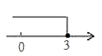 B、
B、 C、
C、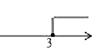 D、
D、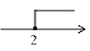 4. 如图,将一个等腰直角三角形放在两条平行线上,若∠1=50°,则∠2的度数为( )
4. 如图,将一个等腰直角三角形放在两条平行线上,若∠1=50°,则∠2的度数为( )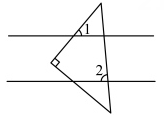 A、75° B、80° C、85° D、90°5. 如图,将周长为8的沿方向平移1个单位得到 , 则四边形的周长为( )
A、75° B、80° C、85° D、90°5. 如图,将周长为8的沿方向平移1个单位得到 , 则四边形的周长为( ) A、4 B、6 C、8 D、106.
A、4 B、6 C、8 D、106.如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(﹣3,2),(b,m),(c,m),则点E的坐标是( )
 A、(2,﹣3) B、(2,3) C、(3,2) D、(3,﹣2)7. 点P(-2,-3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )A、(-3,0) B、(-1,6) C、(-3,-6) D、(-1,0)8. 用加减法解方程组 时,若要求消去 ,则应( )A、 B、 C、 D、9. 我国明代《算法统宗》书中有这样一题:“一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托(一托按照5尺计算).”大意是:现有一根竿和一条绳索,如果用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺,则绳索长几尺?设竿长x尺,绳索长y尺,根据题意可列方程组为( )A、 B、 C、 D、10. 不等式组的整数解的个数是( )A、3个 B、4个 C、5个 D、6个11. 观察下列一组数: , , , , , …,它们是按照一定规律排列的,那么这组数的第个数是( )A、 B、 C、 D、
A、(2,﹣3) B、(2,3) C、(3,2) D、(3,﹣2)7. 点P(-2,-3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )A、(-3,0) B、(-1,6) C、(-3,-6) D、(-1,0)8. 用加减法解方程组 时,若要求消去 ,则应( )A、 B、 C、 D、9. 我国明代《算法统宗》书中有这样一题:“一支竿子一条索,索比竿子长一托,对折索子来量竿,却比竿子短一托(一托按照5尺计算).”大意是:现有一根竿和一条绳索,如果用绳索去量竿,绳索比竿长5尺;如果将绳索对折后再去量竿,就比竿短5尺,则绳索长几尺?设竿长x尺,绳索长y尺,根据题意可列方程组为( )A、 B、 C、 D、10. 不等式组的整数解的个数是( )A、3个 B、4个 C、5个 D、6个11. 观察下列一组数: , , , , , …,它们是按照一定规律排列的,那么这组数的第个数是( )A、 B、 C、 D、二、填空题
-
12. 为了了解线上教学时学校七年级800名学生参加家务劳动的时间,随机对该年级50名学生进行了调查.在这次调查中,样本容量是 .13. 点关于y轴对称的点的坐标是 .14. 如图,桌子上放了一个台灯,台灯主杆 AB 垂直于桌面,调节杆BC连接主杆和灯罩,灯罩CD平行于桌面,则∠ABC+∠BCD=°.
 15. 已知( , 且为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当时,共有2个交点;当时,共有5个交点;当时,共有9个交点;…依此规律,当条直线相交时,共有交点个数为为.
15. 已知( , 且为整数)条直线中只有两条直线平行,且任何三条直线都不交于同一个点.如图,当时,共有2个交点;当时,共有5个交点;当时,共有9个交点;…依此规律,当条直线相交时,共有交点个数为为.
三、解答题
-
16.(1)、计算:23+|﹣3|÷3﹣×5﹣1;(2)、解不等式组并把它的解集在数轴(如图)上表示出来.
 17. 把下列各数填在相应的大括号里:
17. 把下列各数填在相应的大括号里:-4,-|-|,0, , 2 013,-(+5),+1.88,0.010 010 001…(相邻两个1之间0的个数逐次加1),-2.33,….
整数集合{ };
非负数集合{ };
分数集合{ };
无理数集合{ }.
18. 为提倡节约用水,自来水公司实行民用水“阶梯计费"”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行加价收费.为更好地决策,自来水公司随机抽取部分用户的用水量数据,并绘制了如下不完整的统计图(每组数据包括右端点但不包括左端点),请你根据统计图解答下列问题: (1)、此次调查共抽取户用户的用水量数据,扇形统计图中“25-30吨”部分的圆心角为度.(2)、补全频数直方图.(3)、如果自来水公司将基本用水量定为每户25吨,请估计该地区150万用户中享受基本价格的用户数.19. 某校为了落实“阳光体育活动”,在八年级开展了篮球赛.比赛规则是:八年级10个班级每个班级派出一支队伍参赛,赛制采用的是单循环积分赛(每个班级都与其他9个班级进行一场比赛),胜一场积2分,输一场积1分,然后按照积分高低进行排名.赛程过半,小明所在的班级已经进行了5场比赛,积9分.(1)、求小明所在班级胜、负的场次各是多少;(2)、根据分析,总积分超过15分才能确保进入前两名,小明所在班级若想进入前两名在剩下的比赛中至少还要取得几场胜利?20. 如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.
(1)、此次调查共抽取户用户的用水量数据,扇形统计图中“25-30吨”部分的圆心角为度.(2)、补全频数直方图.(3)、如果自来水公司将基本用水量定为每户25吨,请估计该地区150万用户中享受基本价格的用户数.19. 某校为了落实“阳光体育活动”,在八年级开展了篮球赛.比赛规则是:八年级10个班级每个班级派出一支队伍参赛,赛制采用的是单循环积分赛(每个班级都与其他9个班级进行一场比赛),胜一场积2分,输一场积1分,然后按照积分高低进行排名.赛程过半,小明所在的班级已经进行了5场比赛,积9分.(1)、求小明所在班级胜、负的场次各是多少;(2)、根据分析,总积分超过15分才能确保进入前两名,小明所在班级若想进入前两名在剩下的比赛中至少还要取得几场胜利?20. 如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.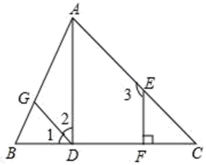
解:∵∠1=∠C,(已知)
∴GD∥ ▲ . ( )
∴∠2=∠DAC.( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF.( )
∴∠ADC=∠ ▲ . ( )
∵EF⊥BC,(已知)
∴∠EFC=90°.( )
∴∠ADC=90°.(等量代换)
21. 如图,在每个小正方形的边长均为1的方格纸中,的顶点都在方格纸的格点上. (1)、将平移后得到 , 图中标出了点的对应点 , 请补全;(2)、连接、 , 则这两条线段之间的关系是;(3)、点为格点,且(点与点不重合),满足这样条件的点有个.22. 如图, ,
(1)、将平移后得到 , 图中标出了点的对应点 , 请补全;(2)、连接、 , 则这两条线段之间的关系是;(3)、点为格点,且(点与点不重合),满足这样条件的点有个.22. 如图, , (1)、试判断与的位置关系,并说明理由.(2)、若是的平分线, , 求的度数.23. 阅读材料:
(1)、试判断与的位置关系,并说明理由.(2)、若是的平分线, , 求的度数.23. 阅读材料:大家知道是无理数,而无理数是无限不循环小数,因此的小数部分我们不可能全部写出来,于是小明用来表示的小数部分,你同意小明的表示方法吗?
事实上,小明的表示方法是有道理的,因为的整数部分是1,将这个数减去其整数部分,差就是小数部分.
又例如:因为 , 即 , 所以的整数部分为2,小数部分为 .
请解答下列问题:
(1)、的整数部分是________,小数部分是________;(2)、如果的小数部分为a,的整数部分为b,求的值;(3)、已知 , 其中m是整数,且 , 求的绝对值.四、实践探究题
-
24. 已知直线 , 点 为平行线 之间的一点, 如图 1 所示,若 平分 平分 .
 (1)、 则 , .(2)、【探究】如图 2 所示, 当点 在直线 的上方时, 若 , 和 的平分线交于点 与 的角平分线交于点 , 与 的角平分线交于点 以此类推, 求 的度数, 并猜想 的度数.
(1)、 则 , .(2)、【探究】如图 2 所示, 当点 在直线 的上方时, 若 , 和 的平分线交于点 与 的角平分线交于点 , 与 的角平分线交于点 以此类推, 求 的度数, 并猜想 的度数.
(3)、【变式】如图 3 所示, 的角平分线的反向延长线和 的补角的角平分线交于点 , 试直接写出 与 的数量关系.