广东省珠海市六校2023-2024学年高一（下）期中数学试卷

试卷更新日期：2024-05-31 类型：期中考试

进入出卷网下载

一、单选题：本题共8小题，每小题5分，共40分。在每小题给出的选项中，只有一项是符合题目要求的。

1. 已知复数 $z = (m + 2) + (m + 1) i$ 在复平面内对应的点在第四象限，则实数 $m$ 的取值范围是（）

A、 $(- 2, - 1)$ B、 $(- \infty, - 2) ∪ (- 1, + \infty)$ C、 $(- 1, + \infty)$ D、 $(- \infty, - 2)$

查看试题解析
2. 在 $△ A B C$ 中，若 $\vec{B A} = \vec{a}$ ， $\vec{B C} = \vec{b}$ ，则 $\vec{C A} =$ ( )

A、 $\vec{a}$ B、 $\vec{a} + \vec{b}$ C、 $\vec{b} - \vec{a}$ D、 $\vec{a} - \vec{b}$

查看试题解析
3. 已知向量 $\vec{a} = (2,4)$ ， $\vec{b} = (m, - 6)$ ，且 $\vec{a} / / \vec{b}$ ，则实数 $m$ 的值为( )

A、 $- 3$ B、 $3$ C、 $8$ D、 $12$

查看试题解析
4. 已知向量 $\vec{a} = (3, 1)$ ， $\vec{b} = (2 k - 1, k)$ ，且 $(\vec{a} + \vec{b}) ⊥ \vec{a}$ ，则 $k$ 的值是
( )

A、 $- 1$ B、 $\frac{3}{7}$ C、 $- \frac{3}{5}$ D、 $\frac{3}{5}$

查看试题解析
5. 已知 $\vec{a}$ 与 $\vec{b}$ 均为单位向量，它们的夹角为 $60 °$ ，那么 $| \vec{a} - 3 \vec{b} |$ 等于( )

A、 $\sqrt{7}$ B、 $\sqrt{10}$ C、 $\sqrt{13}$ D、 $4$

查看试题解析
6. 已知 $\vec{a}, \vec{b}, \vec{c}$ 为非零平面向量，则下列说法正确的是( )

A、 $(\vec{a} \cdot \vec{b}) \cdot \vec{c} = \vec{a} \cdot (\vec{b} \cdot \vec{c})$ B、若 $\vec{a} \cdot \vec{c} = \vec{b} \cdot \vec{c}$ ，则 $\vec{a} = \vec{b}$ C、若 $\vec{a} / / \vec{b}$ ，则 $\exists λ \in R, \vec{b} = λ \vec{a}$ D、 $| \vec{a} \cdot \vec{b} | = | \vec{a} | \cdot | \vec{b} |$

查看试题解析
7. 在 $△ A B C$ 中，角A，B，C所对边分别为 $a, b, c$ ， $A = \frac{π}{3}$ ， $b = 2$ ， $c = 8$ ，则 $\frac{a - 2 b + c}{s i n A - 2 s i n B + s i n C}$ 值等于（）

A、 $\frac{16 \sqrt{3}}{3}$ B、 $4 \sqrt{3}$ C、 $\frac{4 \sqrt{39}}{3}$ D、 $\frac{52 \sqrt{3}}{3}$

查看试题解析
8. 在等边三角形 $A B C$ 的三边上各取一点D，E，F，满足 $D E = 3$ ， $D F = 2 \sqrt{3}$ ， $∠ D E F = 90 °$ ，则三角形 $A B C$ 的面积的最大值是（）

A、 $7 \sqrt{3}$ B、 $13 \sqrt{3}$ C、 $\frac{7}{3} \sqrt{3}$ D、 $\frac{13}{3} \sqrt{3}$

查看试题解析

二、多选题：本题共4小题，共20分。在每小题给出的选项中，有多项符合题目要求。

9. 已知向量 $\vec{a} = (1, - 2), \vec{b} = (3,4)$ ，则( )

A、 $(\vec{a} + \vec{b}) ⊥ \vec{a}$ B、 $(\vec{b} - \vec{a}) / / \vec{b}$ C、 $| \vec{a} + \vec{b} | = 20$ D、与向量 $\vec{a}$ 同向的单位向量是 $(\frac{\sqrt{5}}{5}, - \frac{2 \sqrt{5}}{5})$

查看试题解析
10. 已知复数 $z$ 的共轭复数为 $\bar{z}$ ，则下列说法正确的是( )

A、 $z + \bar{z}$ 一定是实数 B、 $z \cdot \bar{z}$ 一定是实数 C、 $z - \bar{z}$ 一定是纯虚数 D、 $z^{2} = | z |^{2}$

查看试题解析
11. 已知点 $O$ 是 $△ A B C$ 的重心，则下列说法中正确的有( )

A、 $\vec{O A} + \vec{O B} + \vec{O C} = \vec{0}$ B、 $\vec{A O} = \frac{1}{3} (\vec{A B} + \vec{A C})$ C、 $\vec{A O} = \frac{1}{2} (\vec{A B} + \vec{A C})$ D、 $\vec{O B} + \vec{O C} = \frac{1}{6} (\vec{A B} + \vec{A C})$

查看试题解析
12. 在 $△ A B C$ 中，角A，B，C所对的边分别为a，b，c，则下列结论正确的是（）

A、若 $a^{2} + c^{2} - b^{2} > 0$ ，则 $△ A B C$ 为锐角三角形 B、若 $△ A B C$ 为锐角三角形，则 $s i n A > c o s B$ C、若 $s i n 2 A = s i n 2 B$ ，则 $△ A B C$ 为等腰三角形或直角三角形 D、若 $c = a c o s B$ ，则 $△ A B C$ 是直角三角形

查看试题解析

三、填空题：本题共4小题，每小题5分，共20分。

13. 复数 $z$ 满足 $z = \frac{3 + 4 i}{i}$ ，则 $z$ 的虚部为， $| z | =$ .

查看试题解析
14. 已知平面向量 $\vec{a} = (2 m - 1,2)$ ， $\vec{b} = (- 2,3 m - 2)$ ，且 $\vec{a} ⊥ \vec{b}$ ，则 $| 2 \vec{a} - 3 \vec{b} | =$ ．

查看试题解析
15. 已知平面向量 $\vec{a}$ 与 $\vec{b}$ 的夹角为 $\frac{π}{3}$ ，若 $| \vec{a} | = 1$ ， $\vec{b} = (1, 2)$ ，则 $\vec{a}$ 在 $\vec{b}$ 上的投影向量的坐标为.

查看试题解析
16. 在 $△ A B C$ 中， $A B = 2$ ， $∠ C = \frac{π}{3}$ ，则 $\vec{A B} \cdot \vec{A C}$ 的最大值为.

查看试题解析

四、解答题：本题共6小题，共70分。解答应写出文字说明，证明过程或演算步骤。

17. 已知复数 $z_{1} = 1 + a i$ （其中 $a \in R$ 且 $a < 0$ ， i为虚数单位），且 $z_{1}^{2}$ 为纯虚数.

(1)、求实数a的值：

(2)、若 $z_{2} = \frac{z_{1}}{1 + i} + 2$ ，求复数 $z_{2}$ 的共轭复数.

查看试题解析
18. 如图，已知 $A (- 2, 1)$ ， $B (1, 3)$ .

(1)、求线段AB的中点M的坐标；

(2)、若点P是线段AB的一个三等分点，求点P的坐标.

查看试题解析
19. 如图，斜坐标系 $x O y$ 中， $\vec{e_{1}}, \vec{e_{2}}$ 分别是与 $x$ 轴、 $y$ 轴正方向同向的单位向量，且 $\vec{e_{1}}, \vec{e_{2}}$ 的夹角为 $60 °$ ，定义向量 $\vec{O P} = x \vec{e_{1}} + y \vec{e_{2}}$ 在斜坐标系 $x O y$ 中的坐标为有序数对 $(x, y)$ ，记为 $\vec{O P} = x \vec{e_{1}} + y \vec{e_{2}} = (x, y) .$ 在斜坐标系 $x O y$ 中完成下列问题：

(1)、若 $\vec{a} = (2,3)$ ， $\vec{b} = (2, - 1)$ ，求 $\vec{a} \cdot \vec{b}$ ；

(2)、若 $\vec{c} = (x_{0}, y_{0})$ ，求 $| \vec{c} |$ ．

查看试题解析
20. 如图，A、B两点都在河的对岸(不可到达)，若在河岸选取相距20米的C、D两点，测得∠BCA＝60°，∠ACD＝30°，∠CDB＝45°，∠BDA＝60°，那么此时A ， B两点间的距离是多少？

查看试题解析
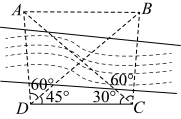21. 在平面直角坐标系中，设向量 $\vec{p} = (c o s A, s i n A)$ ， $\vec{q} = (s i n B, c o s B)$ ，其中 $A$ ， $B$ 分别是 $△ A B C$ 的两个内角．

(1)、若 $\vec{p} / / \vec{q}$ ，求 $C$ 的值；

(2)、若 $\vec{p} \cdot \vec{q} = s i n 2 C$ ， $A B = 2$ ，求 $△ A B C$ 的面积的最大值．

查看试题解析
22. 某校兴趣小组在如图所示的矩形区域 $A B C D$ 内举行机器人拦截挑战赛，在 $E$ 处按 $\vec{E P}$ 方向释放机器人甲，同时在 $A$ 处按 $\vec{A Q}$ 方向释放机器人乙，设机器人乙在 $M$ 处成功拦截机器人甲，两机器人停止运动，若点 $M$ 在矩形区域 $A B C D$ 内 $($ 包含边界 $)$ ，则挑战成功，否则挑战失败 $.$ 已知 $A B = 6$ 米， $E$ 为 $A B$ 中点，比赛中两机器人均匀速直线运动方式行进，记 $\vec{E P}$ 与 $\vec{E B}$ 的夹角为 $θ (0 < θ < π)$ ， $\vec{A Q}$ 与 $\vec{A B}$ 的夹角为 $α (0 < α < \frac{π}{2})$ ．

(1)、若两机器人运动方向的夹角为 $\frac{π}{3}$ ， $A D$ 足够长，机器人乙挑战成功，求两机器人运动路程和的最大值；

(2)、已知机器人乙的速度是机器人甲的速度的 $2$ 倍．
$(i)$ 若 $α = θ = \frac{π}{3}$ ， $A D$ 足够长，求机器人乙能否挑战成功．
$(i i)$ 如何设计矩形区域 $A B C D$ 的宽 $A D$ 的长度，才能确保无论 $θ$ 的值为多少，总可以通过设置机器人乙的释放角度 $α$ 使机器人乙挑战成功？

查看试题解析