湖南省邵阳市新宁县期中联考2023-2024学年八年级下学期数学期中试题

试卷更新日期：2024-05-31 类型：期中考试

进入出卷网下载

一、单选题(每小题3分，共10道小题，合计30分)

1. 下列各组数中，以它们为边长能构成直角三角形的是（）

A、1，3，4 B、2，3，4 C、1，1， $\sqrt{3}$ D、5，12，13

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是 ( )

A、 B、 C、 D、

查看试题解析
3. 矩形具有而平行四边形不一定具有的性质是（）

A、对边相等 B、对角相等 C、对角线相等 D、对角线互相平分

查看试题解析
4. 直角三角形中，两直角边分别是12和5，则斜边上的中线长是 ( )

A、6.5 B、8.5 C、26 D、34

查看试题解析
5. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）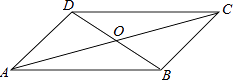

A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB∥DC，AD=BC

查看试题解析
6. 如图所示，在△ABC中，∠ACB=90°，BE平分∠ABC，DE⊥AB于点D，如果AC=3cm，那么AE+DE等于（　　）

A、2cm B、3cm C、4cm D、5cm

查看试题解析
7. 如图，在正方形ABCD中，AE平分∠BAC交BC于点E，点F是边AB上一点，连接DF，若BE=AF，则∠CDF的度数为（）

A、45° B、60° C、67.5° D、77.5°

查看试题解析
8. 如图，在 $△ A B C$ 中，根据尺规作图痕迹，下列说法不一定正确的是（）

A、 $A F = B F$ B、 $A E = \frac{1}{2} A C$ C、 $∠ D B F + ∠ D F B = 90 °$ D、 $∠ B A F = ∠ E B C$

查看试题解析
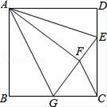
9. 如图，在△ABC中， ∠BAC=90°， AB=3， AC=4， P为边BC上一动点， PE⊥AB于E， PF⊥AC于F， M为EF的中点，则PM的最小值为 ( )

A、2.5 B、2.4 C、1.3 D、1.2

查看试题解析
10. 如图，正方形ABCD中，AB=6，点E在边CD上，且CD=3DE，将△ADE沿AE对折至△AFE，延长EF交边BC于点G，连接AG、CF，则下列结论：
①△ABG≌△AFG；②BG=CG；③AG∥CF；④S_△EGC=S_△AFE；⑤∠AGB+∠AED=145°.

其中正确的个数是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题 (每小题3分，共8道小题，合计24分)

11. 一个正多边形的内角和为 $540 °$ ，则这个正多边形的每一个外角等于度．

查看试题解析
12. 如图，四边形ABCD中， E， F， G， H分别是边AB、BC、CD、DA的中点. 若四边形EFGH为菱形，则对角线AC、BD应满足条件.

查看试题解析
13. 如图，□ABCD的周长为36，对角线AC，BD相交于点 O.点E是CD的中点， $B D = 12,$ 则△DOE的周长为.

查看试题解析
14. 如图，在矩形ABCD中，AC、BD交于点O，DE⊥AC于点E，若∠AOD=110°，则∠CDE=°。

查看试题解析
15. 矩形的两条对角线的夹角为60°，较短的边长为12cm，则矩形的对角线长为cm.

查看试题解析
16. 如图，将长 $8 c m$ ，宽 $4 c m$ 的矩形纸片ABCD折叠，使点A与C重合，则DF的长为．

查看试题解析
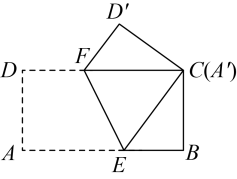17. 如图，在菱形ABCD中，∠B＝45°，E、F分别是边CD，BC上的动点，连接AE、EF，G、H分别为AE、EF的中点，连接GH．若GH的最小值为3，则BC的长为．

查看试题解析
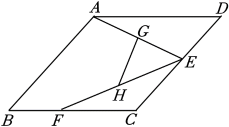18. 如图所示，正方形ABCD的边长为1，其面积标记为 $S_{1},$ 以CD为斜边作等腰直角三角形，以该等腰直角三角形的一条直角边为边向外作正方形，其面积标记为 $S_{2},$ …，按照此规律继续下去，则 $S_{2}_{0}_{2}_{4}$ 的值为.

查看试题解析

三、解答题(19.20题每小题6分, 21.22题每小题8分, 23.24题每小题9分, 25,26题每小题10分)

19. 如图，走廊上有一梯子(AB)以 $45 °$ 的倾斜角斜靠在墙上，墙与地面垂直，梯子影响了行人的行走，工人将梯子挪动位置到(CD)，使其倾斜角变为( $60 ° .$ 如果梯子的长为4米，那么行走的通道拓宽了多少米? (结果保留根号)

查看试题解析
20. 如图，在 $△ A B C$ 中， $C B ⊥ A B, ∠ B A C = 45 °,$ F 是AB延长线上一点，点E在BC上，且. $A E = C F .$ 求证： $△ A B E ≅ △ C B F .$

查看试题解析
21. 如图，已知菱形ABCD的对角线相交于点O，延长CD至点E，使 $D E = C D,$ 连接AE.

(1)、求证： $A E = B D;$

(2)、若 $∠ E = 50 °,$ 求 $∠ D C O$ 的度数.

查看试题解析
22. 如图，已知矩形ABCD，延长CB至点E，使得BE＝BC，对角线AC，BD交于点F，连结EF．

(1)、求证：四边形AEBD是平行四边形；

(2)、若BC＝4，CD＝8，求EF的长．

查看试题解析
23. 如图，在 $△ A B C$ 中， $∠ B A C = 90 °$ ， $A D$ 是 $B C$ 边上的中线，E是 $A D$ 的中点，过点A作 $B C$ 的平行线交 $B E$ 的延长线于点F ，连接 $C F$ ．

(1)、求证：四边形 $A D C F$ 是菱形；

(2)、若 $∠ A C B = 60 °$ ，平行线 $A F$ 与 $B C$ 间的距离为 $4 \sqrt{3}$ ，求菱形 $A D C F$ 的面积．

查看试题解析
24. 如图，在菱形 $A B C D$ 中，对角线 $A C$ ， $B D$ 交于点 $O$ ，过点 $A$ 作 $B C$ 的垂线，垂足为点 $E$ ，延长 $B C$ 到点 $F$ ，使 $C F = B E$ ，连接 $D F$ ．

(1)、求证：四边形 $A E F D$ 是矩形；

(2)、连接 $O E$ ，若 $A D = 25$ ， $O E = 7$ ，求 $A E$ 的长．

查看试题解析
25.
在 $△ A B C$ 中， $∠ A C B = 90 °$ ， $D$ 为 $△ A B C$ 内一点，连接 $B D$ ， $D C$ ，延长 $D C$ 到点 $E$ ，使得 $C E = D C$ ．

(1)、如图 $1$ ，延长 $B C$ 到点 $F$ ，使得 $C F = B C$ ，连接 $A F$ ， $E F .$ 若 $A F ⊥ E F$ ，求证： $B D ⊥ A F$ ；

(2)、连接 $A E$ ，交 $B D$ 的延长线于点 $H$ ，连接 $C H$ ，依题意补全图 $2 .$ 若 $A B^{2} = A E^{2} + B D^{2}$ ，用等式表示线段 $C D$ 与 $C H$ 的数量关系，并证明．

查看试题解析
26. 如图，以点A为旋转中心将正方形ABCD逆时针旋转( $α (0 ° < α < 360 °)$ 角，得到正方形AEFG， $A B = 2 .$ . 作直线BE，过点F作， $F H ⊥ B E,$ 垂足为H，连接DG.

(1)、如图1，当( $α = 60 °$ 时，请直接写出DG和FH的数量关系；

(2)、如图2，当( $α \neq 60 °$ 时，(1)中的结论是否成立，如果成立请证明，如果不成立请说明理由；

(3)、当点E在AD的垂直平分线上时，请直接写出FH 的长度.

查看试题解析