湖南省长沙市长郡集团2024年中考数学模拟考试试卷
试卷更新日期:2024-05-31 类型:中考模拟
一、选择题(在下列各题的四个选项中,只有一项是符合题意的.请在答题卡中填涂符合题意的选项,本大题共10个小题,每小题3分,共30分)
-
1. 图中比数轴上点表示的数大2的数是
 A、 B、0 C、1 D、22. 如图是由一个长方体和一个圆柱组成的几何体,它的俯视图是( )
A、 B、0 C、1 D、22. 如图是由一个长方体和一个圆柱组成的几何体,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 3. 党的二十大报告指出,我国建成世界上规模最大的教育体系、社会保障体系、医疗卫生体系,基本养老保险覆盖十亿四千万人,基本医疗保险参保率稳定在百分之九十五.将数据十亿四千万用科学记数法表示为A、 B、 C、 D、4. 已知某三角形的三边长分别为10,3, , 则的值可以是A、1 B、5 C、7 D、95. 已知一瓶牛奶的营养成分中碳水化合物、蛋白质与脂肪的含量共 , 根据成分表,碳水化合物含量是蛋白质的1.5倍,设蛋白质、脂肪的含量分别为 , , 可列出方程为A、 B、 C、 D、6. 某地学校正评选学生最喜欢的风景胜地,校方进行问卷调查(每人选一个地点),并绘制成如图所示统计图.已知选择楠溪江的有240人,那么选择雁荡山的有
3. 党的二十大报告指出,我国建成世界上规模最大的教育体系、社会保障体系、医疗卫生体系,基本养老保险覆盖十亿四千万人,基本医疗保险参保率稳定在百分之九十五.将数据十亿四千万用科学记数法表示为A、 B、 C、 D、4. 已知某三角形的三边长分别为10,3, , 则的值可以是A、1 B、5 C、7 D、95. 已知一瓶牛奶的营养成分中碳水化合物、蛋白质与脂肪的含量共 , 根据成分表,碳水化合物含量是蛋白质的1.5倍,设蛋白质、脂肪的含量分别为 , , 可列出方程为A、 B、 C、 D、6. 某地学校正评选学生最喜欢的风景胜地,校方进行问卷调查(每人选一个地点),并绘制成如图所示统计图.已知选择楠溪江的有240人,那么选择雁荡山的有 A、90人 B、180人 C、270人 D、360人7. 小红同学在一次作业中完成了以下作图步骤:
A、90人 B、180人 C、270人 D、360人7. 小红同学在一次作业中完成了以下作图步骤:①在和上分别截取 , , 使;
②分别以 , 为圆心,以大于的长为半径作弧,两弧在内交于点;
③作射线 , 连接 , , 如图所示.

根据以上作图,一定可以推得的结论是
A、且 B、且 C、且 D、且8. 某校计划组织研学活动,现有四个地点可供选择:岳麓山、梅溪湖、橘子洲、植物园.若从中随机选择两个地点,则选中“橘子洲”的概率为A、 B、 C、 D、9. 如图1所示为某景区游览路线及方向,①④⑥各路段路程相等,⑤⑦⑧各路段路程相等,②③两路段路程相等.设游玩行走速度恒定,经过每个景点都停留20分钟,小温游路线①④⑤⑥⑦⑧用时3小时25分钟;小州游路线①②⑧,他离入口的路程与时间的关系(部分数据)如图2所示,在2100米处,他到出口还要走10分钟.则路线①③⑥⑦⑧各路段路程之和为
 A、4200米 B、4800米 C、5200米 D、5400米10. “割圆术”孕育了微积分思想,领先世界近千年.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为 , 若用圆内接正十二边形作近似估计,可得的估计值为
A、4200米 B、4800米 C、5200米 D、5400米10. “割圆术”孕育了微积分思想,领先世界近千年.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.如图,的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计的面积,可得的估计值为 , 若用圆内接正十二边形作近似估计,可得的估计值为 A、 B、3 C、 D、
A、 B、3 C、 D、二、填空题(本大题共6个小题,每小题3分,共18分)
-
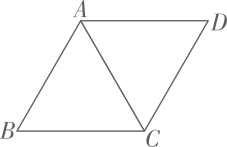
11. 分解因式: .12. 如图,在菱形中, , 则的长为 .
 13. 不等式组的解是。14. 某学校欲招聘一名教师.对甲、乙、丙三名应聘者进行了基础知识、工作经验、语言表达等三方面的测试,他们的各项成绩如下表所示:
13. 不等式组的解是。14. 某学校欲招聘一名教师.对甲、乙、丙三名应聘者进行了基础知识、工作经验、语言表达等三方面的测试,他们的各项成绩如下表所示:项目
应聘者
综合知识
工作经验
语言表达
甲
75
80
80
乙
85
70
80
丙
70
70
78
如果将每位应聘者的综合知识、工作经验、语言表达的成绩按的比例计算其总成绩,并录用总成绩最高的应聘者,则被录用的是 。
15. 若 , 且满足 , 则的值为 .16. 图1是方格绘成的七巧板图案,每个小方格的边长为 , 现将它剪拼成一个“房子”造型(如图 , 过左侧的三个端点作圆,并在圆内右侧部分留出矩形作为题字区域(点 , , , 在圆上,点 , 在上),形成一幅装饰画,则圆的半径为 .
三、解答题(本大题共9个小题,第17、18、19题每题6分,第20、21题每题8分,第22、23题每题9分,第24、25题每题10分,共72分,解答应写出必要的文字说明、证明过程或演算步骤)
-
17. 计算:.18. 先化简,再求值: , 其中 .19. 如图,在的方格纸中,每个小方格的边长为1.已知格点 , 请按要求画格点三角形(顶点均在格点上).
 (1)、在图1中画一个等腰三角形 , 使底边长为 , 点在上,点在上,再画出该三角形绕矩形的中心旋转后的图形;(2)、在图2中画一个 , 使 , 点在上,点在上,再画出该三角形向右平移1个单位后的图形.20. 小明的父亲打算从该公司租一辆汽车外出旅游一天,已知某公司现有 , , 三种型号电动汽车出租,每辆车每天费用分别为300元、380元、500元.旅游的往返行程为 , 为了选择合适的型号,通过网络调查,获得三种型号汽车充满电后的里程数据如图所示.
(1)、在图1中画一个等腰三角形 , 使底边长为 , 点在上,点在上,再画出该三角形绕矩形的中心旋转后的图形;(2)、在图2中画一个 , 使 , 点在上,点在上,再画出该三角形向右平移1个单位后的图形.20. 小明的父亲打算从该公司租一辆汽车外出旅游一天,已知某公司现有 , , 三种型号电动汽车出租,每辆车每天费用分别为300元、380元、500元.旅游的往返行程为 , 为了选择合适的型号,通过网络调查,获得三种型号汽车充满电后的里程数据如图所示. (1)、 小明已经对 , 型号汽车数据统计如表,请继续求出型号汽车的平均里程m、中位数n和众数p;
(1)、 小明已经对 , 型号汽车数据统计如表,请继续求出型号汽车的平均里程m、中位数n和众数p;型号
平均里程
中位数
众数
A
m
n
p
216
215
220
227.5
227.5
225
(2)、为了尽可能避免行程中充电耽误时间,又能经济实惠地用车,请你从相关统计量和符合行程要求的百分比等进行分析,给出合理的用车型号建议.21. 如图,已知矩形ABCD,点在CB延长线上,点在BC延长线上,过点作交ED的延长线于点 , 连结AF交EH于点.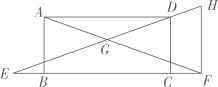 (1)、求证:.(2)、当时,求EF的长.22. 一次足球训练中,小明从球门正前方8m的处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.已知球门高OB为2.44m,现以为原点建立如图所示直角坐标系.
(1)、求证:.(2)、当时,求EF的长.22. 一次足球训练中,小明从球门正前方8m的处射门,球射向球门的路线呈抛物线.当球飞行的水平距离为6m时,球达到最高点,此时球离地面3m.已知球门高OB为2.44m,现以为原点建立如图所示直角坐标系.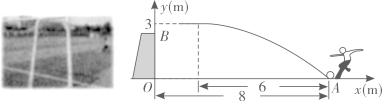 (1)、求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素)。(2)、对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点正上方2.25m处?23. 如图1,为半圆的直径,为延长线上一点,切半圆于点 , , 交延长线于点 , 交半圆于点 , 已知 , . 如图2,连结 , 为线段上一点,过点作的平行线分别交 , 于点 , , 过点作于点 . 设 ,
(1)、求抛物线的函数表达式,并通过计算判断球能否射进球门(忽略其他因素)。(2)、对本次训练进行分析,若射门路线的形状、最大高度均保持不变,则当时他应该带球向正后方移动多少米射门,才能让足球经过点正上方2.25m处?23. 如图1,为半圆的直径,为延长线上一点,切半圆于点 , , 交延长线于点 , 交半圆于点 , 已知 , . 如图2,连结 , 为线段上一点,过点作的平行线分别交 , 于点 , , 过点作于点 . 设 , (1)、求的长和关于的函数表达式;(2)、当 , 且长度分别等于 , , 的三条线段组成的三角形与相似时,求的值;24. 我们定义:点P在一次函数y=ax+b上,点Q在反比例函数上,若存在P、Q两点关于y轴对称,我们称二次函数y=ax2+bx+c为一次函数y=a+b和反比例函数的“幸福函数”,点P称为“幸福点”.例如:点P(﹣1,﹣2)在y=x﹣1上,点Q(1,﹣2)在上,P、Q两点关于y轴对称,此时二次函数y=x2﹣x﹣2为一次函数y=x﹣1和反比例函数的“幸福函数”,点P(﹣1,﹣2)是“幸福点”.(1)、判断一次函数y=x+2和反比例函数是否存在“幸福函数”,若存在,请求出“幸福点”坐标;若不是,请说明理由;(2)、若一次函数y=x﹣k+1与反比例函数只有一个“幸福点”,求其“向光函数”的解析式;(3)、已知一次函数y=ax+b与反比例函数有两个“幸福点”A、B(A在B左侧),其“幸福函数”y=ax2+bx+c与x轴交于C、D两点(C在D左侧),若有以下条件:①a+b+c=0②“幸福函数”经过点(﹣3,4)③a>b>0,记四边形ACBD的面积为S , 求的取值范围.25. 在图1中有Rt , , , 是边上不与 , 重合的一个定点.于点 , 交于点 . 是由线段绕点顺时针旋转得到的, , 的延长线相交于点 .
(1)、求的长和关于的函数表达式;(2)、当 , 且长度分别等于 , , 的三条线段组成的三角形与相似时,求的值;24. 我们定义:点P在一次函数y=ax+b上,点Q在反比例函数上,若存在P、Q两点关于y轴对称,我们称二次函数y=ax2+bx+c为一次函数y=a+b和反比例函数的“幸福函数”,点P称为“幸福点”.例如:点P(﹣1,﹣2)在y=x﹣1上,点Q(1,﹣2)在上,P、Q两点关于y轴对称,此时二次函数y=x2﹣x﹣2为一次函数y=x﹣1和反比例函数的“幸福函数”,点P(﹣1,﹣2)是“幸福点”.(1)、判断一次函数y=x+2和反比例函数是否存在“幸福函数”,若存在,请求出“幸福点”坐标;若不是,请说明理由;(2)、若一次函数y=x﹣k+1与反比例函数只有一个“幸福点”,求其“向光函数”的解析式;(3)、已知一次函数y=ax+b与反比例函数有两个“幸福点”A、B(A在B左侧),其“幸福函数”y=ax2+bx+c与x轴交于C、D两点(C在D左侧),若有以下条件:①a+b+c=0②“幸福函数”经过点(﹣3,4)③a>b>0,记四边形ACBD的面积为S , 求的取值范围.25. 在图1中有Rt , , , 是边上不与 , 重合的一个定点.于点 , 交于点 . 是由线段绕点顺时针旋转得到的, , 的延长线相交于点 . (1)、求证:;(2)、试求的正切值;(3)、如图2,若是的中点,求证: .
(1)、求证:;(2)、试求的正切值;(3)、如图2,若是的中点,求证: .