湖南省常德市津市2024年中考数学一模试卷

试卷更新日期：2024-05-31 类型：中考模拟

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分.每小题只有一个选项是符合题意的）

1. 一元二次方程3x²-4x-4＝1的一次项系数为（）

A、-5 B、-4 C、3 D、6

查看试题解析
2. “明天下雨的概率为 $80 %$ ”，下列对这句话的理解正确的是（）

A、明天一定下雨 B、明天一定不下雨 C、明天80%的地方下雨 D、明天下雨的可能性很大

查看试题解析
3. 二次函数y＝a（x-m）²-k的图象如图所示，下列四个选项中，正确的是（）

A、m＜0，k＜0 B、m＞0，k＞0 C、m＞0，k＜0 D、m＜0，k＞0

查看试题解析
4. 一个圆锥的母线长 $18 c m$ ，底面直径长 $8 c m$ ，则该圆锥的侧面展开图的圆心角为（）

A、 $60 °$ B、 $80 °$ C、 $100 °$ D、 $120 °$

查看试题解析
5. 将二次函数y＝x²-6的图象向右平移1个单位长度，再向下平移3个单位长度，所得图象的解析式为（）

A、y＝x²-2x-5 B、y＝x²+2x-9 C、y＝x²-2x-8 D、y＝x²+2x-5

查看试题解析
6. 七巧板是一种古老的中国传统智力玩具，被誉为“东方魔板”，它是由5个等腰直角三角形、1个正方形和1个平行四边形组成的．如图是由“七巧板”组成的边长为 $5 c m$ 的正方形，若在正方形区域内随意取一点，则该点取到阴影部分的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{7}$ C、 $\frac{1}{8}$ D、 $\frac{2}{7}$

查看试题解析
7. 若将一元二次方程x²-8x+5＝0化成（x+a）²+b＝0的形式，则a和b的值分别为（）

A、4，11 B、4，19 C、-4，-11 D、-4，-19

查看试题解析
8. 如图所示，在平面直角坐标系中A（0，0），B（1，0），P（0，1），四边形ABQP是正方形，把正方形ABQP绕点A顺时针旋转，每次旋转90°，则第2022次旋转结束时，点Q的坐标为（）

A、（1，1） B、（1，-1） C、（-1，-1） D、（-1，1）

查看试题解析
9. 如图， $A B$ 为 $⊙ O$ 的直径， $C$ 为 $⊙ O$ 上一点，过点 $C$ 作 $C D ⊥ A B$ 交 $⊙ O$ 于点 $D$ ，交 $A B$ 于点 $E$ ，连接 $A C$ ， $B D$ ，过点 $C$ 作 $C F ⊥ B D$ 于点 $F$ ，交 $A B$ 于点 $G$ ，若 $C D = 8$ ， $O G = 1$ ，则 $⊙ O$ 的半径为（）

A、 $4$ B、 $\frac{13}{3}$ C、 $\frac{26}{5}$ D、 $6$

查看试题解析
10. 将抛物线y＝-x²+2x+3中x轴上方的部分沿x轴翻折到x轴下方，图象的其余部分不变，得到的新图象与直线y＝x+m有4个交点，则m的取值范围是（）

A、m≤-5 B、 $- \frac{21}{4}$ ≤m＜-5 C、 $- \frac{21}{4} ＜ m ＜ - 3$ D、m≥-3

查看试题解析

二、填空题（共5小题，每小题3分，共15分）

11. 已知关于x的一元二次方程x²-mx+6＝0有一个根为3，则另一个根为.

查看试题解析
12. 某公司购进了一批草莓，并对这批草莓进行了“损坏率”统计，如下表是通过随机取样后，得到的草莓“损坏率”统计表的一部分，由已知数据和图表估计草莓完好的概率为．（精确到 $0.1$ ）
草莓总质量 $n / k g$
损坏草莓质量 $m / k g$
草莓损坏的频率 $m / n$
（精确到 $0.001$ ）
…
…
$200$
$19.8$
$0.099$
$300$
$32.7$
$0.109$
$400$
$40.00$
$0.100$
$500$
$50.62$
$0.101$

查看试题解析
13. 如图，有一张长 $30 c m$ ，宽 $20 c m$ 的矩形纸板，将纸板四个角各剪去一个边长为 $x c m$ 的正方形，然后将四周突出部分折起，可制成一个无盖长方体纸盒，要使制成纸盒的底面积是原来矩形纸板面积的 $\frac{1}{3}$ ，则x的值为．

查看试题解析
14. 已知a，b，c满足a-2b＝c，b+c＝-4a，则二次函数y＝ax²+bx+c（a≠0）的图象的对称轴为直线.

查看试题解析
15. 如图， $A C$ 与 $⊙ O$ 相切于点 $C$ ，线段 $A O$ 交 $⊙ O$ 于点 $B$ ．过点 $B$ 作 $B D ∥ A C$ 交 $⊙ O$ 于点 $D$ ，连接 $C D$ ， $O C$ ，且 $O C$ 交 $D B$ 于点 $E$ ．若 $∠ C D B = 30 °$ ， $D B = 2 \sqrt{3} c m$ ．则图中阴影部分的面积为．

查看试题解析

三、解答题（共8小题，共75分.解答应写出过程）

16. 已知关于x的一元二次方程（m-1）x²-2mx+m+2＝0.

(1)、若方程有实数根，求m的取值范围；

(2)、在等腰△ABC中，一边长为3，其余两边长为方程的两个根，求m的值.

查看试题解析
17. 直线 $y = a x + b (a \neq 0)$ 称作抛物线 $y = a x^{2} + b x (a \neq 0)$ 的关联直线．根据定义回答以下问题：

(1)、求证：抛物线 $y = a x^{2} + b x$ 与其关联直线一定有公共点；

(2)、当 $a = 1$ 时，求抛物线 $y = a x^{2} + b x$ 与其关联直线一定都经过的点的坐标（用字母 $b$ 表示）．

查看试题解析
18. 如图，在 $12 \times 12$ 的正方形网格中，每个小正方形的边长均为1，给出了以格点（网格线的交点）为端点的 $△ A B C$ ．

(1)、以点B为旋转中心，将 $△ A B C$ 顺时针旋转 $180 °$ 得到 $△ A^{'} B C^{'}$ ，画出 $△ A^{'} B C^{'}$ ；

(2)、请你求出点A在（1）中运动的路径长．

查看试题解析
19. 小明和小刚在玩扑克牌的游戏，他们从一副牌中拿出了如图所示的五张扑克牌．

(1)、从一副扑克牌（包含大小王）中随机抽取一张扑克牌，抽到黑桃的概率是多少？

(2)、小明从上图所示的五张扑克牌中随机抽取一张，抽到数字 $6$ 的概率是多少？

(3)、小明先从上图所示的五张扑克牌中抽取一张，放回后小刚再抽取一张，求两张扑克牌上的数字之和小于 $10$ 的概率．

查看试题解析
20. 某电子公司生产并销售一种新型电子产品，经过市场调查发现：每月生产x台电子产品的成本y（元）由三部分组成，分别是生产线投入、材料成本、人工成本，其中生产线投入固定不变为2000元，材料成本（单位：元）与x成正比，人工成本（单位：元）与x的平方成正比，在生产过程中得到如下数据：
x(单位：台)
20
40
y(单位：元)
2104
2216

(1)、求y与x之间的函数关系式；

(2)、若某月平均每台电子产品的成本为26元，求这个月共生产电子产品多少台？

(3)、若每月生产的电子产品均能售出，电子产品的售价也随着x的增大而适当增大，设每台电子产品的售价为Q（单位：元），且有Q＝mx+n（ $m ＜ \frac{1}{100} .$ 且m，n均为常数），已知当x＝2000台时， 0为35元，且此时销售利润W（单位：元）有最大值，求m，n的值.（销售利润＝销售收入-成本）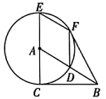

查看试题解析
21. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，以点 $A$ 为圆心， $A C$ 长为半径作 $⊙ A$ ，交 $A B$ 于点 $D$ ，交 $C A$ 延长线于点 $E$ ， $B F$ 是 $⊙ A$ 的切线，连接 $E F ， D F$ ．

(1)、求证： $E F ∥ A B$ ；

(2)、若 $⊙ A$ 的半径为 $2$ ，当四边形 $A D F E$ 为菱形时，求 $B F$ 的长．

查看试题解析
22. 如图，二次函数y＝ax² $- \frac{4}{3} x + c$ 的图象与x轴交于点A（3，0），与y轴交于点B（0，-2）.

(1)、求二次函数的解析式；

(2)、若点P为抛物线上一动点（直线AB上方），且S△PBA＝4，求点P的坐标.

查看试题解析
23. 已知Rt△ABC，∠ACB＝90°，∠BAC＝30°，D是AC边上一点，过点D作DE⊥AB于点E，连接BD，F是BD中点，连接EF，CF.

(1)、如图① ，线段EF，CF之间的数量关系为，∠EFC的度数为；

(2)、如图② ，将△AED绕点A按顺时针方向旋转α（0°＜α＜30°），请判断线段EF，CF之间的数量关系及∠EFC的度数，并说明理由；

(3)、在△AED绕点A旋转的过程中，当点D落到直线AB边上时，连接BE，若BC＝3，AD＝2，请直接写出BE的长度.

查看试题解析

草莓总质量 $n / k g$	损坏草莓质量 $m / k g$	草莓损坏的频率 $m / n$ （精确到 $0.001$ ）
…	…
$200$	$19.8$	$0.099$
$300$	$32.7$	$0.109$
$400$	$40.00$	$0.100$
$500$	$50.62$	$0.101$

x(单位：台)	20	40
y(单位：元)	2104	2216