湖南省长沙市长沙县2023-2024学年七年级下学期数学期中考试试题
试卷更新日期:2024-05-31 类型:期中考试
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
-
1. 下列各数中,为无理数的是( )A、 B、0 C、 D、3.52. 不等式组 的解集在数轴上表示正确的是( )A、
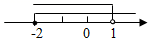 B、
B、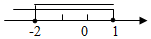 C、
C、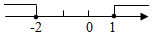 D、
D、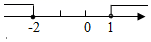 3. 已知a<b , 则一定有﹣2a□﹣2b , “□”中应填的符号是( )A、> B、< C、≥ D、=4. 在平面直角坐标系中,点P(﹣1,2)的位置在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列各式正确的是( )A、 B、 C、 D、6. 在平面直角坐标系中,已知点A在第二象限,点A到x轴的距离为2,到y轴的距离为1,则点A的坐标为( )A、(﹣2,1) B、(2,﹣1) C、(﹣1,2) D、(1,﹣2)7. 已知,如图所示,AB⊥CD , 垂足为O , EF为过O点的一条直线,则∠α与∠β的关系一定成立的是( )
3. 已知a<b , 则一定有﹣2a□﹣2b , “□”中应填的符号是( )A、> B、< C、≥ D、=4. 在平面直角坐标系中,点P(﹣1,2)的位置在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限5. 下列各式正确的是( )A、 B、 C、 D、6. 在平面直角坐标系中,已知点A在第二象限,点A到x轴的距离为2,到y轴的距离为1,则点A的坐标为( )A、(﹣2,1) B、(2,﹣1) C、(﹣1,2) D、(1,﹣2)7. 已知,如图所示,AB⊥CD , 垂足为O , EF为过O点的一条直线,则∠α与∠β的关系一定成立的是( ) A、相等 B、互余 C、互补 D、互为对顶角8. 如图,下列条件中能判定AE∥CD的是( )
A、相等 B、互余 C、互补 D、互为对顶角8. 如图,下列条件中能判定AE∥CD的是( )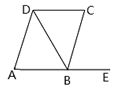 A、∠A=∠C B、∠A+∠ABC=180° C、∠C=∠CBE D、∠A=∠CBE9. 《九章算术》中有这样一个题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?其译文是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱;现有30钱,买得2斗酒.问醇酒、行酒各能买得多少?设醇酒为x斗,行酒为y斗,则可列二元一次方程组为( )
A、∠A=∠C B、∠A+∠ABC=180° C、∠C=∠CBE D、∠A=∠CBE9. 《九章算术》中有这样一个题:“今有醇酒一斗,直钱五十;行酒一斗,直钱一十.今将钱三十,得酒二斗.问醇、行酒各得几何?其译文是:今有醇酒(优质酒)1斗,价值50钱;行酒(劣质酒)1斗,价值10钱;现有30钱,买得2斗酒.问醇酒、行酒各能买得多少?设醇酒为x斗,行酒为y斗,则可列二元一次方程组为( ) A、 B、 C、 D、10. 已知关于x的不等式组有且只有3个整数解,则a的取值范围是( )A、a>﹣1 B、﹣1≤a<0 C、﹣1<a≤0 D、a≤0
A、 B、 C、 D、10. 已知关于x的不等式组有且只有3个整数解,则a的取值范围是( )A、a>﹣1 B、﹣1≤a<0 C、﹣1<a≤0 D、a≤0二、填空题:本题共6小题,每小题3分,共18分。
-
11. ﹣8的立方根是 .
12. 要使代数式2x﹣6的值不大于5x﹣3的值,则x的取值范围是 .13. 如图,在正方形的网格中建立平面直角坐标系,若B、C两点的坐标分别是 , , 则A点的坐标为 . 14. 已知 , 则的值是 .15. m、n为两个连续的整数, , 则m+n= .16. 如图,10块相同的长方形卡片拼成一个大长方形,设长方形卡片的长和宽分别为x和y , 则依题意,列方程组 .
14. 已知 , 则的值是 .15. m、n为两个连续的整数, , 则m+n= .16. 如图,10块相同的长方形卡片拼成一个大长方形,设长方形卡片的长和宽分别为x和y , 则依题意,列方程组 .
三、解答题:本题共9小题,共72分。解答应写出文字说明,证明过程或演算步骤。
-
17. 计算:(1)、;(2)、 .18. 解方程组:(1)、;(2)、 .19. 解不等式并用数轴表示解集: .20. 按要求画图及填空:
在由边长为个单位长度的小正方形组成的网格中建立如图所示平面直角坐标系,原点及的顶点都在格点上.
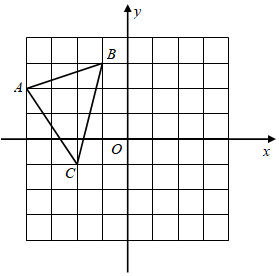 (1)、点的坐标为 .(2)、将先向下平移个单位长度,再向右平移个单位长度得到 , 画出 .(3)、计算的面积.21. 如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.
(1)、点的坐标为 .(2)、将先向下平移个单位长度,再向右平移个单位长度得到 , 画出 .(3)、计算的面积.21. 如图,EF⊥BC,∠1=∠C,∠2+∠3=180°,试说明∠ADC=90°.请完善解答过程,并在括号内填写相应的理论依据.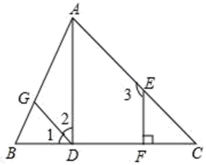
解:∵∠1=∠C,(已知)
∴GD∥ ▲ . ( )
∴∠2=∠DAC.( )
∵∠2+∠3=180°,(已知)
∴∠DAC+∠3=180°.(等量代换)
∴AD∥EF.( )
∴∠ADC=∠ ▲ . ( )
∵EF⊥BC,(已知)
∴∠EFC=90°.( )
∴∠ADC=90°.(等量代换)
22. 已知:如图,C,D是直线AB上两点,∠1+∠2=180°,DE平分∠CDF,EF∥AB.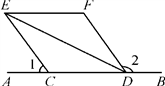 (1)、求证:CE∥DF;(2)、若∠DCE=130°,求∠DEF的度数.23. 某汽车专卖店销售A , B两种型号的新能源汽车.上周售出2辆A型车和3辆B型车,销售额为114万元.本周已售出3辆A型车和2辆B型车,销售额为106万元.(1)、求每辆A型车和B型车的售价各为多少万元?(2)、甲公司拟向该店购买A , B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,通过计算说明有哪几种购车方案?24. 阅读下列材料:
(1)、求证:CE∥DF;(2)、若∠DCE=130°,求∠DEF的度数.23. 某汽车专卖店销售A , B两种型号的新能源汽车.上周售出2辆A型车和3辆B型车,销售额为114万元.本周已售出3辆A型车和2辆B型车,销售额为106万元.(1)、求每辆A型车和B型车的售价各为多少万元?(2)、甲公司拟向该店购买A , B两种型号的新能源汽车共6辆,且A型号车不少于2辆,购车费不少于130万元,通过计算说明有哪几种购车方案?24. 阅读下列材料:关于x、y的方程:ax+by=c , 当b≠0时,我们可用含x的代数式表示y , 则原方程可变成y=﹣ , 我们将变形后的式子叫做原方程的“一次凤凰式”,其中﹣品叫做K系数,叫做L系数,例如:3x+5y=7,则可变成y=﹣x+ . 则K=﹣ , L=
(1)、二元一次方程3x﹣2y=1的“一次凤凰式”为 .(2)、关于x、y的二元一次方程mx+2y=3,当满足K+L≤4时,求m的取值范围;(3)、关于x、y的方程﹣6x+(n﹣1)y=3,当满足K系数与L系数都为正整数时,求整数n的取值.25. 在平面直角坐标系中,A(a , 0),B(1,b),a , b满足 , 连接AB交y轴于C . (1)、直接写出a= , b=;(2)、如图1,点P是x轴上一点,且三角形ABP的面积为12,求点P的坐标;(3)、如图2,直线BD交x轴于D(4,0),将直线BD平移经过点A , 交y轴于E , 点Q(x , y)在直线AE上,且三角形ABQ的面积不超过三角形ABD面积的 , 求点Q横坐标x的取值范围.
(1)、直接写出a= , b=;(2)、如图1,点P是x轴上一点,且三角形ABP的面积为12,求点P的坐标;(3)、如图2,直线BD交x轴于D(4,0),将直线BD平移经过点A , 交y轴于E , 点Q(x , y)在直线AE上,且三角形ABQ的面积不超过三角形ABD面积的 , 求点Q横坐标x的取值范围.