江西省宜春市上高第二名校2023-2024学年高一下学期3月月考试题

试卷更新日期：2024-05-31 类型：月考试卷

进入出卷网下载

一、选择题（4分一个，共44分，1-7单选，8-11多选。）

1. 在物理学建立、发展的过程中，许多物理学家的科学发现推动了人类历史的进步。关于科学家和他们的贡献，下列说法中正确的是（）

A、牛顿认为在足够高的高山上以足够大的水平速度抛出一物体，物体就不会再落在地球上 B、英国物理学家牛顿利用“扭秤实验”首先较准确的测定了万有引力常量 C、伽利略用“月—地检验”证实了万有引力定律的正确性 D、德国天文学家开普勒对伽利略观测的行星数据进行了多年研究，得出了开普勒三大行星运动定律

查看试题解析
2. 如图所示，一位同学玩飞镖游戏。圆盘最上端有一点P ，飞镖抛出时与P等高，且距离P点为L。当飞镖以初速度 $v_{0}$ 垂直盘面瞄准P点抛出的同时，圆盘以经过盘心O点的水平轴在竖直平面内匀速转动。忽略空气阻力，重力加速度为g ，若飞镖恰好击中P点，则（　　）

A、飞镖击中P点所需的时间为 $\frac{L}{2 v_{0}}$ B、圆盘的半径为 $\frac{g L^{2}}{2 v_{0}^{2}}$ C、圆盘转动角速度的最小值为 $\frac{2 π v_{0}}{L}$ D、P点随圆盘转动的线速度可能为 $\frac{3 π g L}{4 v_{0}}$

查看试题解析
3. 如图所示，一倾斜的匀质圆盘绕垂直于盘面的固定对称轴以恒定的角速度转动，盘面上离转轴一定距离处有一小物体与圆盘始终保持相对静止。下列说法正确的是（　　）

A、物体在最高点时静摩擦力的方向一定指向圆心 B、物体在最低点时静摩擦力的方向可能背向圆心 C、物体在最高点时静摩擦力可能是运动过程中的最大值 D、物体在最低点时静摩擦力一定是运动过程中的最大值

查看试题解析
4. 火星绕太阳运转可看成是匀速圆周运动，设火星运动轨道的半径为r ，火星绕太阳一周的时间为T ，万有引力常量为G ，则下列说法正确的是（）

A、火星的质量 $m_{火} = \frac{4 π^{2} r^{3}}{G T^{2}}$ B、火星的向心加速度 $a_{火} = \frac{4 π^{2} r}{T^{2}}$ C、太阳的平均密度 $ρ_{太} = \frac{3 π}{G T^{2}}$ D、太阳的质量 $m_{太} = \frac{4 π^{2} r}{G T^{2}}$

查看试题解析
5. 在如图所示的皮带传送装置中，A、B分别为传动轮边缘上的两点，C为大轮上的一固定点，三点对应的轨道关系为R_A=2R_B=2R_C ，传动过程中皮带不打滑。则下列A、B、C三点的线速度v、角速度ω、向心加速度a_n的大小关系正确的是（）

A、v_A：v_B：v_C=1：1：2 B、ω_A：ω_B：ω_C=1：2：2 C、a_nA：a_nB：a_nC=2：4：1 D、a_nA：a_nB：a_nC=2：2：1

查看试题解析
6. 地球的公转轨道接近圆，天文学中计量天体之间距离时常将地球和太阳的平均距离记为一天文单位，以1AU表示，彗星的运动轨道是一个非常扁的椭圆。天文学家哈雷曾经跟踪过一颗彗星，并预言这颗彗星将每隔一定时间就会再次出现。1948年观察到它离地球最远，1986年离地球最近，则彗星近日点和远日点之间的距离最接近于（　　）

A、10AU B、20AU C、40AU D、80AU

查看试题解析
7. 如图所示，半径为R的半球形陶罐，固定在可以绕竖直轴转动的水平转台上，转台转轴与过陶罐球心O的对称轴 $O O^{'}$ 重合。转台以一定角速度匀速转动，一质量为m的小物块落入陶罐内，经过一段时间后小物块随陶罐一起转动且相对罐壁静止，此时小物块受到的摩擦力恰好为0，且它和O点的连线与 $O O^{'}$ 之间的夹角 $θ$ 为 $60 °$ ，重力加速度为g。下列说法不正确的是（）

A、物块做圆周运动的加速度大小为 $\sqrt{3} g$ B、陶罐对物块的弹力大小为 $2 m g$ C、转台转动的角速度大小为 $\sqrt{\frac{2 g}{R}}$ D、如果转台的转速稍稍增大，小物块相对罐壁有向下的运动趋势

查看试题解析
8. 关于在水平公路上转弯的摩托车，下列说法正确的是（　　）

A、摩托车转弯时由重力、支持力、牵引力的合力提供向心力 B、摩托车转弯时由静摩擦力提供向心力 C、若摩托车转弯时的速度过大，则摩托车会向弯道外侧运动 D、若摩托车转弯时的速度过大，则摩托车会向弯道内侧运动

查看试题解析
9. 2021年2月，执行我国火星探测任务的天问一号探测器在成功实施三次近火制动后，进入了如图所示的椭圆形停泊轨道，其中 $A B$ 为长轴， $C D$ 为短轴，O为椭圆轨道的中心。已知天问一号在此轨道的公转周期为T ，则下列说法正确的是（　　）

A、天问一号在A点的线速度小于在B点的线速度 B、天问一号在A点的加速度大于在B点的加速度 C、根据开普勒第三定律可得： $\frac{O D^{3}}{T^{2}} = k$ ， k的值仅与中心天体火星有关 D、天问一号从C点到A点所需的时间小于 $\frac{T}{4}$

查看试题解析
10. 如图所示，长为 $l$ 的轻杆，一端固定一个小球；另一端固定在光滑的水平轴上，使小球在竖直平面内做圆周运动，小球过最高点的速度为v，下列叙述中正确的是（　　）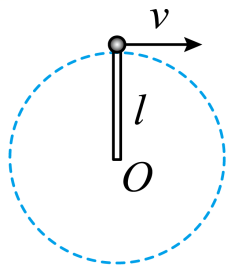

A、v的值必须大于等于 $\sqrt{g l}$ B、当v由零逐渐增大时，小球在最高点所需向心力也逐渐增大 C、当v由 $\sqrt{g l}$ 值逐渐增大时，杆对小球的弹力逐渐增大 D、当v由 $\sqrt{g l}$ 值逐渐减小时，杆对小球的弹力逐渐减小

查看试题解析
11. 如图所示，现有一光滑角形框架 $O A B$ ， $O A$ 边竖直放置，夹角 $θ = 30 °$ ，质量 $m$ 的小球套在 $O B$ 杆上，并通过长为 $l$ 的轻绳悬吊于 $M$ 点，小球静止时轻绳与 $O A$ 杆的夹角也为 $θ$ ，现让框架以 $O A$ 为轴，以不同的角速度 $ω$ 匀速转动，小球均能在水平面内做匀速圆周运动。已知重力加速度大小为 $g$ ，下列说法正确的是（　　）

A、框架静止时，小球受到绳的拉力大小为 $\sqrt{3} m g$ B、 $O B$ 杆对小球的弹力不可能为0 C、绳上无弹力时， $ω$ 的范围是 $\sqrt{\frac{\sqrt{3} g}{l}} \leq ω \leq \sqrt{\frac{2 \sqrt{3} g}{l}}$ D、绳上无弹力时， $ω$ 越大，小球做圆周运动的半径越大

查看试题解析

二、实验题（2分一空，共18分）

12. 如图所示是向心力演示仪的示意图，匀速转动手柄1，可使变速塔轮2和3以及长槽4和短槽5随之匀速转动，槽内的小球做匀速圆周运动。球对挡板6的作用力使弹簧测力套筒7下降，标尺8露出红白相间的标记，向心力大小与标尺露出的等分格的格数成正比。

(1)、本实验所采用的探究方法与下列哪个实验是相同的____（填选项序号）；

A、探究两个互成角度的力的合成规律 B、探究加速度与物体受力、物体质量的关系 C、探究平抛运动的特点

(2)、图中小球做圆周运动的向心力来源于；标尺上的等分格数之比显示出两个小球所受向心力的（填“比值”或“大小”）；

(3)、某次实验皮带套的左右两个塔轮的半径之比 $r_{2} : r_{3} = 3 : 1$ ， A、B两球（质量相同）运动半径相同，则A、B两球的角速度之比为，左右标尺露出的等分格的格数之比为。

查看试题解析
13. 2023年《三体》电视剧异常火爆，这正展示了人类想了解未知世界的渴望，为延续人类文明防患于未然，人类也需要寻找适宜人类居住的新家园。假设多年后宇航员找到了一类地星球，为了探究星球的相关情况，宇航员降落在星球表面，并做了以下实验（假设该星球为匀质球体，星球半径为R）：

(1)、实验Ⅰ：让一石子和一片羽毛分别从相同高度由静止同时释放多次，发现两者总沿竖直方向向下运动并同时落在水平地面上。由此可以判断该星球表面（填“有”或“无”）大气。

(2)、实验Ⅱ：在赤道的水平地面上，以一定的水平速度 $v_{0}$ 抛出物体，并记录下抛出点的高度h及相应的从抛出到落地过程中的水平位移x，保持 $v_{0}$ 不变，改变高度，重复实验多次。并用描点法做出了图像，你认为宇航员做图像最为合理。（选填选项前的相应字母）
A． $h - x$ B． $h^{2} - x$ C． $h - x^{2}$
若求出图线的斜率为 $k_{1}$ ，则赤道处的重力加速度 $g =$ 。

(3)、实验Ⅲ：到达极地后，在抛出速度与实验Ⅱ中 $v_{0}$ 一样的情况下，重复实验Ⅱ，若得到图像的斜率为 $k_{2}$ 。据此宇航员推出了该类地星球的自转周期 $T =$ 。（用 $k_{1}$ 、 $k_{2}$ 、R、 $v_{0}$ 表示）

查看试题解析

三、解答题（9+9+10+10）

14. 一轿车以30 m/s的速率沿半径为60 m的圆形跑道行驶，当轿车从A运动到B时，轿车与圆心的连线转过的角度为90°，求：

(1)、轿车的周期多大；

(2)、此过程中轿车通过的路程是多少；

(3)、轿车运动过程中的向心加速度是多大。

查看试题解析
15. 如图所示为固定在竖直平面内的光滑轨道DCBA ，其中CBA部分是半径。R=0.4m的半圆形轨道（AC 是圆的直径），DC 部分是水平轨道。一个质量：m=0.5kg的小球沿水平方向进入轨道，通过最高点A后落在水平轨道上，已知落地瞬间速度方向与水平成45°角。小球运动过程中所受空气阻力忽略不计，g取10m/s²。求：

(1)、小球经过A点的速度大小；

(2)、小球落地点与C点间的水平距离；

(3)、小球在A 点时轨道对小球的压力大小。

查看试题解析
16. 《天问》是我国战国时期诗人屈原创作的一首长诗，全诗问天问地问自然，表达了作者对传统的质疑和对真理的探索精神，2021年5月15日7时18分，我国第一颗人造火星探测器“天问一号”成功着陆于火星南部预选着陆区。若火星和地球绕太阳的运动均可视为匀速圆周运动，已知火星公转轨道半径与地球公转轨道半径之比为3 ∶2，火星的质量约为地球的0.1倍，半径约为地球的0.5倍，地球表面的重力加速度大小为g ，忽略火星大气阻力，忽略火星的自转。质量为m的“天问一号”着陆器在着陆火星前，会在火星表面附近经历一个时长为t₀、速度由v₀减速到零的过程，若该减速过程可视为一个竖直向下的匀减速直线运动，求：

(1)、火星和地球绕太阳运动的线速度大小之比；

(2)、火星表面的重力加速度大小；

(3)、此过程中着陆器受到的制动力大小约为多少？

查看试题解析
17. A、B两颗卫星在同一轨道平面内绕地球做匀速圆周运动。地球半径为R，A卫星离地面的高度为R，周期为T，B卫星离地面高度为3R，则：（结果可用根式表示）

(1)、A、B两卫星周期之比是多少？

(2)、若某时刻两卫星正好通过地面同一点的正上方，则经过多长时间两卫星再次相距最近？

(3)、若某时刻两卫星正好通过地面同一点的正上方，则经过多长时间两卫星相距最远？

查看试题解析