广西壮族自治区崇左市宁明县2023-2024学年七年级下学期数学期中考试试卷
试卷更新日期:2024-05-31 类型:期中考试
一、单项选择题(本大题共12小题,每小题3分,共36分)
-
1. 4的平方根是( )A、2 B、 C、4 D、2. 下列实数中,是无理数的是( )A、 B、 C、 D、3. 不等式的解集在数轴上表示正确的是()A、
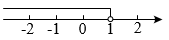 B、
B、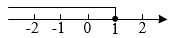 C、
C、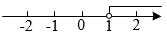 D、
D、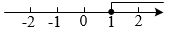 4. 清代袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )A、 B、 C、 D、5. 如果x<y , 那么下列不等式变形正确的是( )A、 B、 C、 D、6. 如图,A , B , C , D是数轴上的四个点,这四个点中最适合表示的是( )
4. 清代袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )A、 B、 C、 D、5. 如果x<y , 那么下列不等式变形正确的是( )A、 B、 C、 D、6. 如图,A , B , C , D是数轴上的四个点,这四个点中最适合表示的是( ) A、点A B、点B C、点C D、点D7. 下列运算正确的是( )A、 B、 C、 D、8. 已知有一个数值转换器,其流程如图所示,当输入x的值是时,输出y的值是( )
A、点A B、点B C、点C D、点D7. 下列运算正确的是( )A、 B、 C、 D、8. 已知有一个数值转换器,其流程如图所示,当输入x的值是时,输出y的值是( ) A、 B、 C、 D、9. 不等式组的整数解有( )A、1个 B、2个 C、3个 D、4个10. 如图,甲、乙、丙、丁四名同学给出了四种表示该长方形面积的多项式:①;②;③;④ . 你认为正确的有( )
A、 B、 C、 D、9. 不等式组的整数解有( )A、1个 B、2个 C、3个 D、4个10. 如图,甲、乙、丙、丁四名同学给出了四种表示该长方形面积的多项式:①;②;③;④ . 你认为正确的有( ) A、①② B、①③ C、①②③ D、①②③④11. 设 , , 则M与N的大小关系为( )A、 B、 C、 D、不能确定12. 若 , 则的值是( )A、8 B、12 C、24 D、36
A、①② B、①③ C、①②③ D、①②③④11. 设 , , 则M与N的大小关系为( )A、 B、 C、 D、不能确定12. 若 , 则的值是( )A、8 B、12 C、24 D、36二、填空题(本大题共6小题,每小题2分,共12分)
-
13. 比较大小: . (填“>”或“<”或“=”)14. 计算的结果为 .15. 化简的结果为 .16. 已知长方形的面积为 , 宽为2a , 则长方形的长为 .17. 若 , , 则 .18. 若关于x , y的二元一次方程组 , 的解满足 , 则m的取值范围是 .
三、解答题(本大题共8小题,共72分.解答应写出文字说明、证明过程或演算步骤)
-
19. 计算: .20. 已知一个正数的平方根是和 , 的立方根是2,求:(1)、a , b的值;(2)、的算术平方根.21. 先化简,再求值: , 其中 , .22. 解不等式(组):(1)、解不等式:;(2)、解不等式组 , 并把它的解集在数轴上表示出来.
 23. 阅读材料后解决问题.
23. 阅读材料后解决问题.小明遇到下面一个问题:计算 . 经过观察,小明发现如果将原式进行恰当地变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:
.
请你根据小明解决问题的方法,试着解决以下的问题:
计算:
(1)、(2)、 .24. 若(且 , m , n都是正整数),则 .利用上述结论解决下列问题:
(1)、若求n的值;(2)、若求x的值.25. 围棋起源于中国,古代称为“弈”,是棋类鼻祖,围棋距今已有四千多年的历史.中国象棋也是中华民族的文化瑰宝,它源远流长,趣味浓厚,基本规则简明易懂.某学校为丰富学生课余生活,计划到甲超市购买一批象棋和围棋.已知购买4副象棋和6副围棋共需280元,购买8副象棋和2副围棋共需260元.(1)、求每副象棋和围棋的单价;(2)、若学校准备购买象棋和围棋共90副,总费用不超过2512元,那么最多能购买多少副围棋?26. 请认真观察图形,解答下列问题: (1)、根据图中条件,你能得到怎样的等量关系?请用等式表示出来;(2)、如果图中的a , 满足 , , 分别求;的值;(3)、已知 , 求的值.
(1)、根据图中条件,你能得到怎样的等量关系?请用等式表示出来;(2)、如果图中的a , 满足 , , 分别求;的值;(3)、已知 , 求的值.