初中数学同步训练必刷培优卷(北师大版七年级下册 5.3简单的轴对称图形)
试卷更新日期:2024-05-30 类型:同步测试
一、选择题
-
1. 如图是由11个等边三角形拼成的六边形.若最小等边三角形的边长为 ,最大等边三角形的边长为 ,则 与 的关系为( )
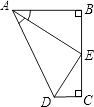
 A、 B、 C、 D、2. 如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:
A、 B、 C、 D、2. 如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:①∠AED=90° ②∠ADE=∠CDE ③DE=BE ④AD=AB+CD,
四个结论中成立的是( )
 A、①②④ B、①②③ C、②③④ D、①③3. 如图,已知∠AOB是直角,∠AOC是锐角,ON平分
A、①②④ B、①②③ C、②③④ D、①③3. 如图,已知∠AOB是直角,∠AOC是锐角,ON平分
∠AOC,OM平分∠BOC,则∠MON是( ) A、45º B、45º+∠AOC C、60°-∠AOC D、不能计算
A、45º B、45º+∠AOC C、60°-∠AOC D、不能计算二、填空题
-
4. 如图,已知 , 点在射线上运动,点在射线上运动.和的角平分线交于点 , 、分别为、上的点,和的角平分线交于点 . 若点A、B在运动过程中,存在中有一个角是另一个角的2倍,则的度数为 .
 5. 有一副直角三角板和 , 其中 , , 如图所示叠放,边点边交于点 , 过点作平分 , 若 , 则度.
5. 有一副直角三角板和 , 其中 , , 如图所示叠放,边点边交于点 , 过点作平分 , 若 , 则度. 6. 如图,已知等边三角形的边长为12cm,甲,乙两动点同时从顶点出发,甲以1厘米/秒的速度沿等边三角形的边按顺时针方向移动,乙以3厘米/秒的速度沿等边三角形的边按逆时针方向移动,相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动.则第二次相遇时乙与最近顶点的距离是厘米.
6. 如图,已知等边三角形的边长为12cm,甲,乙两动点同时从顶点出发,甲以1厘米/秒的速度沿等边三角形的边按顺时针方向移动,乙以3厘米/秒的速度沿等边三角形的边按逆时针方向移动,相遇后甲乙的速度均增加1厘米/秒且都改变原方向移动.则第二次相遇时乙与最近顶点的距离是厘米. 7. 已知:如图,∠ABC=40°,点P是射线BC上一动点,把△ABP沿AP折叠,B点的对应点为点D,当直线AD垂直于BC时,∠ABD=°.
7. 已知:如图,∠ABC=40°,点P是射线BC上一动点,把△ABP沿AP折叠,B点的对应点为点D,当直线AD垂直于BC时,∠ABD=°. 8. 如图,在△ABC中,∠ACB=60°,∠ABC= (20°< <120°),AE平分△ABC的外角∠BAD,CF将∠ACB分成1:2两部分.若AE、CF交于点G,则∠AGC的度数为(用含 的代数式表示).
8. 如图,在△ABC中,∠ACB=60°,∠ABC= (20°< <120°),AE平分△ABC的外角∠BAD,CF将∠ACB分成1:2两部分.若AE、CF交于点G,则∠AGC的度数为(用含 的代数式表示).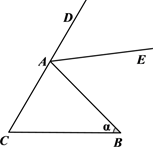 9. 如图,在等腰三角形ABC中,BC=3cm,△ABC的面积是18cm²,腰AB的垂直平分线EF交AC于点F,若点D为BC边上的中点,M为EF上的动点,则△BDM周长的最小值为 。
9. 如图,在等腰三角形ABC中,BC=3cm,△ABC的面积是18cm²,腰AB的垂直平分线EF交AC于点F,若点D为BC边上的中点,M为EF上的动点,则△BDM周长的最小值为 。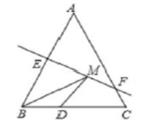 10. 在△ABC中,AB=AC,把△ABC折叠,使点B与点A重合,折痕交AB于点M,交BC于点N.如果△CAN是等腰三角形,则∠B的度数为 .11. 在△ABC 中, AB = AC , ∠BAC=100°,点 D 在 BC 上, △ABD 和△AFD 关于直线 AD 对称, ∠FAC 的平分线交 BC 于点 G , 连接 FG 当∠BAD =.时,△DFG为等腰三角形.
10. 在△ABC中,AB=AC,把△ABC折叠,使点B与点A重合,折痕交AB于点M,交BC于点N.如果△CAN是等腰三角形,则∠B的度数为 .11. 在△ABC 中, AB = AC , ∠BAC=100°,点 D 在 BC 上, △ABD 和△AFD 关于直线 AD 对称, ∠FAC 的平分线交 BC 于点 G , 连接 FG 当∠BAD =.时,△DFG为等腰三角形.
三、作图题
-
12. 仅用无刻度的直尺作出符合下列要求的图形.
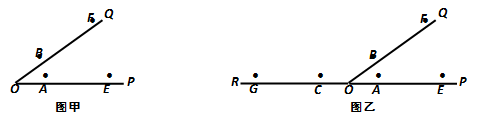 (1)、如图甲,在射线OP、OQ上已截取OA=OB,OE=OF.试过点O作射线OM,使得OM将∠POQ平分;(2)、如图乙,在射线OP、OQ、OR上已截取OA=OB=OC,OE=OF=OG(其中OP、OR在同一根直线上). 试过点O作一对射线OM、ON,使得OM⊥ON.
(1)、如图甲,在射线OP、OQ上已截取OA=OB,OE=OF.试过点O作射线OM,使得OM将∠POQ平分;(2)、如图乙,在射线OP、OQ、OR上已截取OA=OB=OC,OE=OF=OG(其中OP、OR在同一根直线上). 试过点O作一对射线OM、ON,使得OM⊥ON.四、解答题
-
13. 已知:直线EF分别与直线AB , CD相交于点G , H , 并且∠AGE+∠DHE=180°.
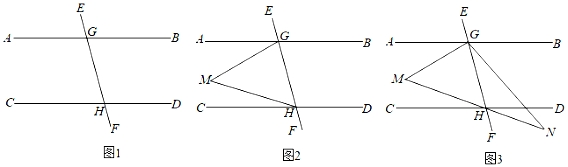 (1)、如图1,求证:AB∥CD;(2)、如图2,点M在直线AB , CD之间,连接GM , HM , 求证:∠M=∠AGM+∠CHM;(3)、如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N , 连接GN , 若∠N=∠AGM , ∠M=∠N+∠FGN , 求∠MHG的度数.14. 如图1,已知直线 , 点为直线AB,ED之间(不在直线上)的一个动点,连接CB,CD,BE平分平分和DA交于点 .
(1)、如图1,求证:AB∥CD;(2)、如图2,点M在直线AB , CD之间,连接GM , HM , 求证:∠M=∠AGM+∠CHM;(3)、如图3,在(2)的条件下,射线GH是∠BGM的平分线,在MH的延长线上取点N , 连接GN , 若∠N=∠AGM , ∠M=∠N+∠FGN , 求∠MHG的度数.14. 如图1,已知直线 , 点为直线AB,ED之间(不在直线上)的一个动点,连接CB,CD,BE平分平分和DA交于点 . (1)、证明: ,(2)、如图2,连接CF,则在点的运动过程中,当满足时:
(1)、证明: ,(2)、如图2,连接CF,则在点的运动过程中,当满足时:①若 , 求的度数;
②若 , 求的度数.
五、实践探究题
-
15. 综合与实践
如图,直线 , 直线与 , 分别交于点 , , 将一个含角的直角三角板按如图放置,使点 , 分别在直线 , 上, , , .
 (1)、的度数为 ;(2)、若的平分线交直线于点 , 如图 .
(1)、的度数为 ;(2)、若的平分线交直线于点 , 如图 .当 , 时,求的度数;
将三角板保持并向左平移,求在平移的过程中 ▲ 用含的式子表示 .
16. 阅读材料:两个三角形各有一个角互为对顶角,这两个三角形叫做对顶三角形.解决问题:如图,与是对顶三角形.
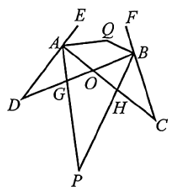 (1)、试说明:;(2)、试利用上述结论解决下列问题:
(1)、试说明:;(2)、试利用上述结论解决下列问题:若、分别平分与 , , ,
①求的度数(用含m、n的代数式表示);
②若、分别平分与 , , 求的取值范围.
六、综合题
-
17. 在中, , 点是直线上一点不与、重合 , 以为一边在的右侧作 , 使 , , 连接E .(1)、如图1,当点在线段上,如果 .

①则与全等吗?请说明理由;
②求的度数;
(2)、如图2,如果 , 当点在线段上移动,则的度数是; (3)、如图2,当点在线段上,如果 , 点为中边上的一个动点与、均不重合 , 当点运动到什么位置时,的周长最小?18. 已知直线分别与直线 , 交于点 , , 平分交直线于点 , 且 , 点是射线上的一个动点(不与点 , 重合),平分 , 交直线于点 , 过点作 , 交于点 , 设 , .
(3)、如图2,当点在线段上,如果 , 点为中边上的一个动点与、均不重合 , 当点运动到什么位置时,的周长最小?18. 已知直线分别与直线 , 交于点 , , 平分交直线于点 , 且 , 点是射线上的一个动点(不与点 , 重合),平分 , 交直线于点 , 过点作 , 交于点 , 设 , . (1)、如图①,求证;(2)、如图②,当点H在点F的右侧时, , 求的度数.
(1)、如图①,求证;(2)、如图②,当点H在点F的右侧时, , 求的度数.
-