贵州省2023-2024学年七年级下学期数学期末考试仿真试卷(二)
试卷更新日期:2024-05-30 类型:期末考试
一、选择题
-
1. 计算 的结果为( )A、 B、 C、 D、2. 在平面直角坐标系中,点 位于( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列是二元一次方程组的是( )A、 B、 C、 D、4. 下列调查中,最适宜全面调查的是( )A、检测某城市的空气质量 B、检查一枚运载火箭的各零部件 C、调查某款节能灯的使用寿命 D、调查观众对春节联欢晚会的满意度5. 不等式组的解集在数轴上可表示为( ).A、
 B、
B、 C、
C、 D、
D、 6. 把一块直尺与一块三角板如图放置,若 , 则的度数为( )
6. 把一块直尺与一块三角板如图放置,若 , 则的度数为( ) A、 B、 C、 D、7. 给出下列4个命题,其中真命题的个数为( )
A、 B、 C、 D、7. 给出下列4个命题,其中真命题的个数为( )①对顶角相等;②互补的两个角中一定是一个为锐角,另一个为钝角;③同旁内角相等,两直线平行;④同旁内角的两个角的平分线互相垂直.
A、1 B、2 C、3 D、48. 在平面直角坐标系中,点A的坐标为 , 平行于y轴,且 , 则点B的坐标为( )A、 B、 C、或 D、或9. 估计的值应在( )A、0和1之间 B、1和2之间 C、2和3之间 D、3和4之间10. 关于x的不等式12﹣3x≥0的非负整数解共有( )个.A、3 B、4 C、5 D、611. 某商场新购进一种服装,每套售价1000元,若将裤子降价10%,上衣涨价5%,调价后这套服装的单价比原来提高了2%,则调价前上衣的单价是( )A、200元 B、480元 C、600元 D、800元二、填空题
-
12. 若用表示第3排第2座,则第5排第4座可表示为 .13. 比较大小:25 . (填“>”、“<”或“=”)14. 欢欢观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=115°,则∠E的度数是°.
 15. 如图,点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……,按这样的运动规律,经过第2025次运动后动点P的坐标是 .
15. 如图,点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……,按这样的运动规律,经过第2025次运动后动点P的坐标是 .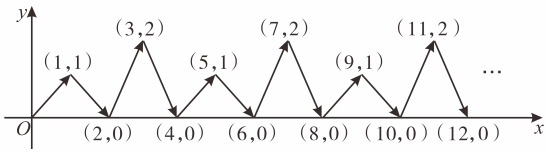
三、解答题
-
16. 计算(1)、a-2 b2 (a2 b-2 )-3(2)、17. (1)解方程组
(2)解不等式组
18. 如图在平面直角坐标系中,已知点 , C , A , . (1)、直接写出点A , C , 的坐标;(2)、求三角形的面积;(3)、将三角形平移后,点的对应点为 , 画出平移所得的三角形 .19. 为了进一步了解某校八年级学生的身体素质情况,体育老师抽测了该校八年级(1)班50名学生一分钟的跳绳次数,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:请结合图表完成下列问题:
(1)、直接写出点A , C , 的坐标;(2)、求三角形的面积;(3)、将三角形平移后,点的对应点为 , 画出平移所得的三角形 .19. 为了进一步了解某校八年级学生的身体素质情况,体育老师抽测了该校八年级(1)班50名学生一分钟的跳绳次数,以测试数据为样本,绘制出部分频数分布表和部分频数分布直方图,图表如下所示:请结合图表完成下列问题:组别
次数
频数(人数)
第1组
6
第2组
8
第3组
第4组
18
第5组
6
 (1)、本次调查为(填全面调查或抽样调查),样本容量为;(2)、 ▲ ;并把频数分布直方图补充完整;(3)、若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳不合格的人数大约有多少?20. 请把下列解题过程补充完整并在括号中注明理由:
(1)、本次调查为(填全面调查或抽样调查),样本容量为;(2)、 ▲ ;并把频数分布直方图补充完整;(3)、若在一分钟内跳绳次数少于120次的为测试不合格,则该校八年级共1000人中,一分钟跳绳不合格的人数大约有多少?20. 请把下列解题过程补充完整并在括号中注明理由:如图, , , , 求.

解: , , ( ▲ )
又 , , ( ▲ )
, ( ▲ )
▲ , ( ▲ )
, ▲ .
21. 如图,平分 . (1)、判断与是否平行,并说明理由.(2)、若 , 求的度数.22. 某蔬菜种植基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.
(1)、判断与是否平行,并说明理由.(2)、若 , 求的度数.22. 某蔬菜种植基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.(1)改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元?
(2)已知改造1个甲种型号大棚的时间是5天,改造1个乙种型号大概的时间是3天,该基地计划改造甲、乙两种蔬菜大棚共8个,改造资金最多能投入128万元,要求改造时间不超过35天,请问有几种改造方案?哪种方案基地投入资金最少,最少是多少?
23. 已知:如图, . (1)、如图1所示:点为上一点, , 直接写出与的数量关系;(2)、如图2,平分 , 的反向延长线与的平分线交于点,若比大 , 求的度数;(3)、保持(2)中所求的的度数不变,如图3,平分 , 平分 , 作 , 求的度数.
(1)、如图1所示:点为上一点, , 直接写出与的数量关系;(2)、如图2,平分 , 的反向延长线与的平分线交于点,若比大 , 求的度数;(3)、保持(2)中所求的的度数不变,如图3,平分 , 平分 , 作 , 求的度数.