贵州省2023-2024学年七年级下学期数学期末考试仿真试卷（一）

试卷更新日期：2024-05-30 类型：期末考试

进入出卷网下载

一、选择题

1. 计算 ${(\frac{1}{2024})}^{- 1}$ 的值为( )

A、 $- \frac{1}{2024}$ B、 $\frac{1}{2024}$ C、-2024 D、2024

查看试题解析
2. 要画一个面积为 $30 c m^{2}$ 长方形，其长为 $x c m$ ，宽为 $y c m$ ，在这一变化过程中，常量与变量分别为（）

A、常量为30，变量为x、y B、常量为30、y ，变量为x C、常量为30、x ，变量为y D、常量为x、y ，变量为30

查看试题解析
3. 下列各图中， $∠ 1$ 与 $∠ 2$ 是对顶角的是（）

A、 B、 C、 D、

查看试题解析
4. 在一些美术字中，有的汉字是轴对称图形．下面4个汉字中，可以看作是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
5. 我国自主研发的28nm浸没式光刻机的成功问世，标志着我国在光刻机领域迈出了坚实的一步，已知28nm为0.000 000 028米，数据0.000 000 028用科学记数法表示为（）

A、 $2.8 \times 1 0^{- 14}$ B、 $2.8 \times 1 0^{- 8}$ C、 $2.8 \times 1 0^{- 5}$ D、 $2.8 \times 1 0^{- 9}$

查看试题解析
6. 在下列各组数据中，不能作为直角三角形三边边长的是（）

A、 $3$ ， $4$ ， $5$ B、 $3$ ， $3$ ， $5$ C、 $5$ ， $12$ ， $13$ D、 $6$ ， $8$ ， $10$

查看试题解析
7. 把一块直尺与一块三角板如图放置，若 $∠ 1 = 42 °$ ，则 $∠ 2$ 的度数为（）

A、 $125 °$ B、 $120 °$ C、 $130 °$ D、 $132 °$

查看试题解析
8. 已知 ${(a + b)}^{2} = 7$ ， ${(a - b)}^{2} = 3$ ，则 $a b$ 的值为（）

A、1 B、2 C、4 D、 $\sqrt{10}$

查看试题解析
9. 若 $∠ 1$ 和 $∠ 2$ 互补， $∠ 1 = 136 °$ ，则 $∠ 2$ 的度数是（）

A、 $44 °$ B、 $46 °$ C、 $54 °$ D、 $56 °$

查看试题解析
10. 如图， $A B ∥ C D$ ， OE平分 $∠ B O C$ ， OF平分 $∠ B O D$ ， $O P ⊥ A B$ ， $∠ A B O = 50 °$ ，则下列结论：① $∠ B O E = 60 °$ ；② $O F ⊥ O E$ ；③ $∠ P O F = ∠ B O E$ ；④ $∠ B O D = 2 ∠ P O E$ ；⑤ $∠ C O E = 65 °$ .其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. “二十四节气”是上古农耕文明的智慧结晶，被国际气象界誉为“中国第五大发明”．若要从“二十四节气”主题邮票中的“立春”“芒种”“秋分”“大寒”四张邮票中随机抽取两张，则恰好抽到“芒种”和“秋分”两张邮票的概率是．

查看试题解析
12. 计算：（2a+b）（2a﹣b）＝．

查看试题解析
13. 已知a，b互为相反数，c，d互为倒数， $| m | = 2$ ，则 $\frac{a + b}{m} - m^{2} + 2 c d$ 的值是.

查看试题解析
14. 某中学开展春季越野赛，小明、小颖两名同学同时从起点出发，他们所跑的路程y（千米）与时间x（分）之间的关系如图所示，小刚由图示得出下列信息：①在比赛中小明的速度始终比小颖快，所以小明先到达终点；②比赛开始20分钟时，小明和小颖第一次相遇；③越野赛全程为6千米；④小明最后冲刺速度为 $0.3$ 千米/分钟．在小刚得出的信息中正确的有（填序号即可）．

查看试题解析

三、解答题

15. 计算。

(1)、 ${(- 1)}^{2017} + {(\frac{1}{2})}^{- 2} + {(3.14 - π)}^{0}$

(2)、 ${(- 2 x^{2})}^{3} + 4 x^{3} \cdot x^{3}$

查看试题解析
16. 先化简，再求值： $(a + b) (a - b) - {(a - b)}^{2} + 2 b^{2}$ ，其中 $a = - 3 ， b = \frac{1}{2}$ ．

查看试题解析
17. 某市发行福利彩票3000万元，每张彩票面值2元，设特等奖10个，一等奖50个，二等奖100个，三等奖100个．小李买了一张彩票．求：

(1)、小李中特等奖的概率．

(2)、小李中特等奖或一等奖的概率．

(3)、小李中奖的概率.

查看试题解析
18. 如图， $△ A B C ≅ △ D E B$ ，点E在边 $A B$ 上， $D E$ 与 $A C$ 相交于点 $F$ ．若 $D E = 9 ， B C = 4$ ， $∠ D = 2 5^{∘} ， ∠ C = 7 0^{∘}$ ．

(1)、求线段 $A E$ 的长；

(2)、求 $∠ D B C$ 的度数．

查看试题解析
19. 如图，在边长为1的小正方形组成的网格中，点A、B、C均在小正方形的顶点上.

(1)、在图中画出与△ABC关于直线 $l$ 成轴对称的 $△ A^{^{'}} B^{^{'}} C^{^{'}}$ ；

(2)、在直线 $l$ 上找一点 $P$ ，使得 $△ B P C$ 的周长最小；

(3)、求 $△ A^{^{'}} B^{^{'}} C^{^{'}}$ 的面积.

查看试题解析
20. 如图，在 $△ A B C$ 中， $D E$ 垂直平分 $A B$ ，分别交 $A B$ 、 $B C$ 于点 $D$ 、 $E$ ， $A E$ 平分 $∠ B A C$ ， $∠ B = 30 °$ .

(1)、求 $∠ C$ 的度数；

(2)、若 $D E = 2$ ，求 $B C$ 的长.

查看试题解析
21. 小明和妈妈一起在一条笔直的跑道上锻炼身体，到达起点后小明做了一会准备活动，妈妈先跑 $.$ 当小明出发时，妈妈已经距离起点 $200$ 米 $.$ 他们距起点的距离 $s ($ 米 $)$ 与小明出发的时间 $t ($ 秒 $)$ 之间的关系如图所示，根据图中给出的信息解答下列问题：

(1)、小明出发之后，前 $70$ 秒的速度是米 $/$ 秒；妈妈的速度是米 $/$ 秒；

(2)、 $a$ 表示的数字是；

(3)、直接写出小明出发后的 $110$ 秒内，两人何时相距 $60$ 米．

查看试题解析
22. 【阅读材料】“数形结合”是一种非常重要的数学思想方法．比如：在学习“整式的乘法”时，我们通过构造几何图形，用“等积法”直观地推导出了完全平方和公式： ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ （如图1）．利用“数形结合”的思想方法，可以从代数角度解决图形问题，也可以用图形关系解决代数问题．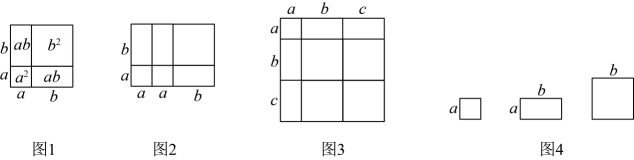
【方法应用】根据以上材料提供的方法，完成下列问题：

(1)、由图2可得等式：；由图3可得等式：；

(2)、利用图3得到的结论，解决问题：若 $a + b + c = 15$ ， $a b + a c + b c = 35$ ，则 $a^{2} + b^{2} + c^{2} =$ ；

(3)、如图4，若用其中 $x$ 张边长为 $a$ 的正方形， $y$ 张边长为 $b$ 的正方形， $z$ 张边长分别为a、b的长方形纸片拼出一个面积为 $(2 a + b) (a + 2 b)$ 长方形（无空隙、无重叠地拼接），则 $x + y + z =$ ．

查看试题解析
23. 前山河部分水域的两岸是互相平行的直线，在两岸的 $M 、 N$ 处分别设置了一盏可以不断匀速旋转地探照灯．设两岸 $A B ∥ C D$ ，点M处探照灯射出的光线自 $M B$ 开始顺时针旋转，点N处探照灯射出的光线自 $C N$ 开始顺时针旋转，当两灯射出的光线旋转至各自岸边时立即反向旋转，旋转中常常出现交叉照射，若点M处射出的光线每秒旋转a度，点N处射出的光线每秒旋转b度，且 $| a + b - 6 | + \sqrt{(2 a - b)^{2}} = 0$ ．

(1)、求 $a, b$ 的值；

(2)、设点M处探照灯先旋转20秒后，记两盏灯一起旋转的时间为t秒，当点M处探照灯射出的光线 $M P$ 首次旋转至 $M A$ 位置之前，能否出现两盏探照灯射出的光线互相平行，若能，求出所有t的值：若不能，说明理由；

(3)、已知 $M N$ 垂直河岸，设两灯同时开始旋转，若两盏探照灯射出的光线在河面上点F处互相垂直，求 $∠ M N F$ 的度数；

查看试题解析