2024年广东省中考数学全真模拟试卷(四)
试卷更新日期:2024-05-30 类型:中考模拟
一、选择题:本大题共10小题,每小题3分,共30分,每小题有4个选项,只有一个选项正确
-
1. - 的倒数是( )A、- B、 C、-3 D、32. 若 , 与互余,则( )A、 B、 C、 D、3. 预计到2025年我国高铁运营里程将达到385000千米,将数据385000用科学记数法表示为( )A、3.85×106 B、3.85×105 C、38.5×105 D、0.385×1064. 如图所示,直线 , 则( )
 A、 B、 C、 D、5. 如图是一款桌面可调整的学习桌,桌面宽度AB为60cm,桌面平放时高度DE为70cm,若书写时桌面适宜倾斜角的度数为 , 则桌沿(点A)处到地面的高度h为( )
A、 B、 C、 D、5. 如图是一款桌面可调整的学习桌,桌面宽度AB为60cm,桌面平放时高度DE为70cm,若书写时桌面适宜倾斜角的度数为 , 则桌沿(点A)处到地面的高度h为( )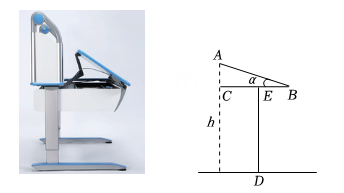
A、 B、 C、 D、6. 如题图,在矩形中,点E在上,连接 , 将沿翻折,使点D落在边上的点F处.若 , , 则的值为( ) A、 B、 C、 D、7. 如图,内接于 , , , 为的直径, , 那么的值为( )
A、 B、 C、 D、7. 如图,内接于 , , , 为的直径, , 那么的值为( ) A、4 B、 C、 D、28. 如图所示,是矩形的对角线的中点,为的中点.若 , , 则的周长为( )
A、4 B、 C、 D、28. 如图所示,是矩形的对角线的中点,为的中点.若 , , 则的周长为( ) A、10 B、 C、 D、149. 孙子算经中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺,木长多少尺?若设绳子长x尺,木长y尺,所列方程组正确的是( )A、 B、 C、 D、10. 如图,在等腰梯形中, , , , 点沿从点出发向点匀速移动.过点作 , 交折线于点 , 记的面积为y , 则关于时间的函数图象大致是( )
A、10 B、 C、 D、149. 孙子算经中有一道题,原文是:“今有木,不知长短,引绳度之,余绳四尺五寸;屈绳量之,不足一尺,木长几何?”意思是:用一根绳子去量一根长木,绳子还剩余尺;将绳子对折再量长木,长木还剩余尺,木长多少尺?若设绳子长x尺,木长y尺,所列方程组正确的是( )A、 B、 C、 D、10. 如图,在等腰梯形中, , , , 点沿从点出发向点匀速移动.过点作 , 交折线于点 , 记的面积为y , 则关于时间的函数图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题:本大题共5小题,每小题3分,共15分
-
11. 因式分解:x2y﹣y= .12. 如图,等边内接于 , , 则图中阴影部分的面积等于 .
 13. 如图,在中, , , 于点 , , 则 .
13. 如图,在中, , , 于点 , , 则 .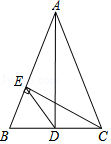 14. 如图,点A,C为函数图象上的两点,过A,C分别作轴,轴,垂足分别为B,D,连接 , , , 线段交于点E,且点E恰好为的中点.当的面积为时,k的值为 .
14. 如图,点A,C为函数图象上的两点,过A,C分别作轴,轴,垂足分别为B,D,连接 , , , 线段交于点E,且点E恰好为的中点.当的面积为时,k的值为 .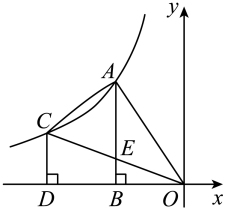 15. 如图,平行四边形中以点为圆心,适当长为半径作弧,交、于、 , 分别以点、为圆心,大于长为半径作弧,两弧交于点 , 连接并延长,与交于点 , 若AB=5,CE=4,DE=3,则的长为 .
15. 如图,平行四边形中以点为圆心,适当长为半径作弧,交、于、 , 分别以点、为圆心,大于长为半径作弧,两弧交于点 , 连接并延长,与交于点 , 若AB=5,CE=4,DE=3,则的长为 .
三、解答题(一):本大题共3小题,第16题10分,第17、18题各7分,共24分.
-
16.(1)、解一元一次不等式组;(2)、已知一次函数的图象经过点 , , 求这个函数的解析式.17. 如图,线段AB,CD分别表示甲、乙建筑物的高,AB⊥MN于点B,CD⊥MN于点D,两座建筑物间的距离BD为35m.若甲建筑物的高AB为20m,在点A处测得点C的仰角α为45°,则乙建筑物的高CD为多少m?
 18. 周末,小明和他的爸爸来到环形运动场进行跑步锻炼,绕环运动场一圈的路程为400米.
18. 周末,小明和他的爸爸来到环形运动场进行跑步锻炼,绕环运动场一圈的路程为400米. (1)、若两人同时同起点相向而跑,则经过36秒后首次相遇;若两人同时同起点同向而跑,则经过180秒后,爸爸首次从后面又追上小明,问小明和他的爸爸的速度各为多少?(2)、假设爸爸的速度是6米/秒,小明的速度是5米/秒,两人进行400米赛跑,同时同起点同向出发,等爸爸跑到半圈时,故意降速为4米/秒,按此继续比赛,小明能否在400米终点前追上爸爸,如果能,求追上时距离终点还有多少米;如果不能,请说明理由.
(1)、若两人同时同起点相向而跑,则经过36秒后首次相遇;若两人同时同起点同向而跑,则经过180秒后,爸爸首次从后面又追上小明,问小明和他的爸爸的速度各为多少?(2)、假设爸爸的速度是6米/秒,小明的速度是5米/秒,两人进行400米赛跑,同时同起点同向出发,等爸爸跑到半圈时,故意降速为4米/秒,按此继续比赛,小明能否在400米终点前追上爸爸,如果能,求追上时距离终点还有多少米;如果不能,请说明理由.四、解答题(二):本大题共3小题,每小题9分,共27分.
-
19. 如图,点 , , , 在网格的格点上,每小方格是边长为1个单位长度的正方形.请按要求画图,并回答问题:
 (1)、过点画直线的垂线,垂足为;并直接写出点到直线的距离;(2)、过点画交于点;(3)、请写出图中的所有同位角.20. 某校学生的上学方式分为“A步行、B骑车、C乘公共交通工具、D乘私家车、E其它”,该校数学兴趣小组成员在全校随机抽取了若干名学生进行抽样调查,并整理样本数据,得到如下两幅不完整的统计图:
(1)、过点画直线的垂线,垂足为;并直接写出点到直线的距离;(2)、过点画交于点;(3)、请写出图中的所有同位角.20. 某校学生的上学方式分为“A步行、B骑车、C乘公共交通工具、D乘私家车、E其它”,该校数学兴趣小组成员在全校随机抽取了若干名学生进行抽样调查,并整理样本数据,得到如下两幅不完整的统计图: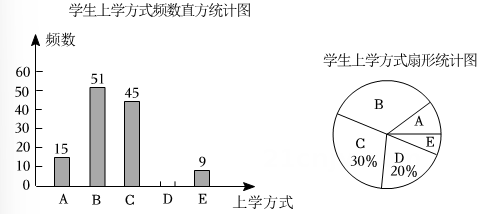 (1)、本次抽样调查的人数为 人,并补全条形统计图;(2)、扇形统计图中“A步行”上学方式所对的圆心角是度;(3)、若该校共2000名学生,请估计该校“B骑车”上学的人数约是人;(4)、该校数学兴趣小组成员结合调查获取的信息,向学校提出了一些建议.
(1)、本次抽样调查的人数为 人,并补全条形统计图;(2)、扇形统计图中“A步行”上学方式所对的圆心角是度;(3)、若该校共2000名学生,请估计该校“B骑车”上学的人数约是人;(4)、该校数学兴趣小组成员结合调查获取的信息,向学校提出了一些建议.如:骑车上学的学生超过全校学生总人数的30%,建议学校合理安排自行车停车场地.
请你结合上述统计的全过程,再提出一条合理化建议.
21. 综合与实践素材一:某款遮阳棚(图1),图2、图3是它的侧面示意图,点为墙壁上的固定点,摇臂绕点旋转过程中长度保持不变,遮阳棚可自由伸缩,棚面始终保持平整.米.

素材二:该地区某天不同时刻太阳光线与地面的夹角的正切值:
时刻(时)
12
13
14
15
角的正切值
5
2.5
1.25
1
【问题解决】
(1)、如图2,当时,这天12时在点位置摆放的绿萝刚好不被阳光照射到,求绿萝摆放位置与墙壁的距离;(2)、如图3,旋转摇臂 , 使得点离墙壁距离为1.2米,为使绿萝在这天12时时都不被阳光照射到,则绿萝摆放位置与墙壁的最远距离是多少?五、解答题(三):本大题共2小题,每小题12分,共24分.

