2024年广东省中考数学全真模拟试卷(三)

试卷更新日期：2024-05-30 类型：中考模拟

进入出卷网下载

一、选择题(本大题共10小题，每小题3分，共30分，每小题有4个选项，只有一个选项正确)

1. 如图的几何体由五个相同的小正方体搭成，它的主视图是（）

A、 B、 C、 D、

查看试题解析
2. 经历百年风雨，中国共产党从小到大、由弱到强，从建党时 $50$ 多名党员，发展成为今天已经拥有超过 $9800$ 万党员的世界第一大政党． $9800$ 万用科学记数法表示为( )

A、 $9.8 \times 10^{6}$ B、 $98 \times 10^{6}$ C、 $9.8 \times 10^{7}$ D、 $0.98 \times 10^{8}$

查看试题解析
3. 新能源汽车是我国经济发展的重要产业之一，下列新能源车标中，不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 我市为了方便市民绿色出行，推出了共享单车服务．图①是某品牌共享单车放在水平地面的实物图，图②是其示意图，其中AB，CD都与地面l平行，∠BCD＝60°，∠BAC＝50°，当∠MAC为（）度时，AM∥BE．

A、15 B、65 C、70 D、115

查看试题解析
5. 某种蓄电池的电压 $U$ （单位： $V$ ）为定值，使用蓄电池时，电流 $I$ （单位： $A$ ）与电阻 $R$ （单位： $Ω$ ）是反比例函数关系．当 $R = 5$ 时， $I = 8$ ，则当 $R = 10$ 时， $I$ 的值是（　　）

A、4 B、5 C、10 D、0

查看试题解析
6. 下列运算正确的是（）

A、 $a^{4} \cdot a^{3} = a^{12}$ B、 $3 a^{2} - 2 a^{2} = 1$ C、 $4 a^{3} \div 2 a^{3} = 2 a$ D、 ${(- 3 a)}^{3} = - 27 a^{3}$

查看试题解析
7. 已知 $α$ 、 $β$ 是关于 $x$ 的一元二次方程 $x^{2} + (2 m + 3) x + m^{2} = 0$ 的两个不相等的实数根，且满足 $\frac{1}{α} + \frac{1}{β} = - 1$ ，则 $m$ 的值是( )

A、 $3$ B、 $1$ C、 $3$ 或 $- 1$ D、 $- 3$ 或 $1$

查看试题解析
8. 如图，点A在函数 $y = \frac{3}{x} (x > 0)$ 的图像上，点B在函数 $y = \frac{5}{x} (x > 0)$ 的图像上，且 $A B ∥ x$ 轴， $B C ⊥ x$ 轴于点 $C$ ，则四边形 $A B C O$ 的面积为（）

A、1 B、2 C、 $\frac{7}{2}$ D、 $\frac{5}{2}$

查看试题解析
9. 如图，正方形ABCD内接于 $⊙ O$ ，点P在 $\overset{⌢}{A B}$ 上，则 $∠ P$ 的度数为（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $90 °$

查看试题解析
10. 如图，在矩形 $A B C D$ 中， $B C = 1$ ， $∠ A D B = 60 °$ ，动点P沿折线 $A D \to D B$ 运动到点B ，同时动点Q沿折线 $D B \to B C$ 运动到点C ，点 $P ， Q$ 在矩形边上的运动速度为每秒1个单位长度，点P ， Q在矩形对角线上的运动速度为每秒2个单位长度．设运动时间为t秒， $△ P B Q$ 的面积为S ，则下列图象能大致反映S与t之间函数关系的是（）

A、 B、 C、 D、

查看试题解析

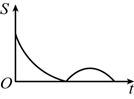
二、填空题(本大题共5小题，每小题3分，共15分)

11. 分解因式： $2 x^{2} - 2 x =$ ．

查看试题解析
12. 如图，在菱形 $A B C D$ 中， $E$ 为 $C D$ 边上的一点，且 $C E = \frac{1}{4} C D$ ，连接 $B E$ ，与对角线 $A C$ 交于点 $F$ ，则 $△ C E F$ 的面积与 $△ A B F$ 的面积之比为.

查看试题解析
13. “春节”期间，某服装商店举行促销活动，全部商品八折销售，小华购买一件标价为140元的运动服，打折后他比按原价购买节省了元．

查看试题解析
14. 如图，把两根钢条 $O A ， O B$ 的一个端点连在一起，点C，D分别是 $O A ， O B$ 的中点，若 $C D = 3 cm$ ，则该工件内槽宽 $A B$ 的长为cm．

查看试题解析
15. 如图，分别过点 $P_{i} (i, 0) (i = 1 、 2 、 \cdot \cdot \cdot 、 2023)$ 作 $x$ 轴的垂线，交 $y = x^{2}$ 的图象于点 $A_{i}$ ，交直线 $y = - x$ 于点 $B_{i}$ ，则 $\frac{1}{A_{1} B_{1}} + \frac{1}{A_{2} B_{2}} + \frac{1}{A_{3} B_{3}} + \cdot \cdot \cdot + \frac{1}{A_{2023} B_{2023}}$ 的值为．

查看试题解析

三、解答题(一)(本大题共3小题，共24分，其中第16题10分，第17题7分，第18题7分)

16. （1）解方程： $2 x^{2} - 3 x + 1 = 0$
（2）化简： $\frac{a - 2}{a} + \frac{a^{2} + 4 a + 4}{a^{2}} \cdot \frac{a}{a + 2}$

查看试题解析
17. （综合与实践）下图是 $6 \times 6$ 的正方形网格，每个小正方形的边长为1，每个小正方形的顶点称为格点，回答下列问题.（要求：作图只用无刻度的直尺）

(1)、作 $∠ A O B$ ，使得 $c o s ∠ A O B = \frac{3}{5}$ ；

(2)、作出 $∠ A O B$ 的角平分线 $O C$ ，并简要说明点 $C$ 的位置是如何找到的（不用证明）.

查看试题解析
18. 在平面直角坐标系中，一次函数y=kx+b与反比例函数y= $\frac{6}{x}$ 的图象在第一象限交于点A（1，a），B（b，3），求一次函数y=kx+b的表达式。

查看试题解析

四、解答题(二)(本大题共3小题，共27分，每题9分)

19. 为了丰富学生在学校的课余生活，学校开展了合唱、手工、机器人编程、书法这四项活动（依次用A ， B ， C ， D表示），为了解学生对以上四项活动的喜好程度，学校随机抽取部分同学进行了“你最喜欢哪一项活动”的问卷调查，要求必选且只选一种．并根据调查结果绘制了如图条形统计图和扇形统计图：

(1)、请补全条形统计图；

(2)、估计全校3000名学生中最喜欢手工活动的人数约为人；

(3)、现从喜好机器人编程的甲、乙、丙、丁四名学生中任选两人搭档加入活动策划会，请用树状图或列表法求恰好甲和丁同时被选到的概率．

查看试题解析
20. “元旦”期间，某电商想购进 $A 、 B$ 两种商品出售，已知每件 $B$ 种商品的进价比每件 $A$ 种商品的进价少5元，且用400元购进 $A$ 种商品的数量是用100元购进 $B$ 种商品数量的2倍．

(1)、求每件 $A$ 种商品和每件 $B$ 种商品的进价分别是多少元？

(2)、商店决定购进 $A 、 B$ 两种商品共80件， $A$ 种商品加价5元出售， $B$ 种商品比进价提高 $20 %$ 后出售，要使所有商品全部出售后利润不少于200元，求 $A$ 种商品至少购进多少件？

查看试题解析
21. 综合与实践：【问题情境】：通过查看出厂包装袋上的数据，数学活动小组的同学发现 $A 4$ 纸的长与宽分别为 $297 m m$ 和 $210 m m$ ，其比值为 $\frac{297}{210} \approx 1.414$ ，而 $\sqrt{2} \approx 1.414$ ，他们上网查阅资料也发现 $A 4$ 纸的长与宽的比是一个特殊值“ $\sqrt{2}$ ” $.$ 不妨定义长与宽的比为 $\sqrt{2} ： 1$ 的矩形为“标准矩形” $.$ 【操作实践】：如图 $1$ ，数学活动小组的同学在几何画板软件上画了一个正方形 $A B C D$ ，连接对角线 $B D$ ，在射线 $D C$ 上截取了 $D E = D B$ ，过点 $E$ 作 $E F ⊥ A B$ 交 $A B$ 的延长线于点 $F$ ，令 $A B = 1$ ．
【问题探究】：

(1)、求证：四边形 $A F E D$ 为“标准矩形”；

(2)、如图 $2$ ，数学活动小组的同学在图 $1$ 的基础上隐藏了线段 $B C$ ，在线段 $E F$ 上取一点 $P$ ，连接 $B P$ ， $D P$ ．
$①$ 当 $D P$ 平分 $∠ B D E$ 时，求 $P F$ 的长；
$②$ 当 $△ B D P$ 的周长最小时，求 $∠ P B F$ 的正切值．

查看试题解析

五、解答题(三)(本大题共2小题，每小题12分，共24分)

22. 综合运用
如图，直线 $y = \sqrt{3} x + 6$ 与y轴、x轴分别交于A、B两点，点C的坐标为 $(6, 0)$ ，点P是线段 $B C$ 上一点且点P与点O不重合．过A、O、P三点的圆与直线 $y = \sqrt{3} x + 6$ 交于点D．连接 $A C$ 交圆于点E．

(1)、求 $∠ B A C$ 的度数；

(2)、当 $△ A D E$ 和 $△ A B C$ 相似时，求点P的坐标；

(3)、设点P的横坐标为m， $\sqrt{2} A D ＋ A E$ 的值是定值吗？若是，求出该定值；若不是，用含m的式子表示．

查看试题解析
23. 如图，平面内的两条直线l₁、l₂ ，点A、B在直线l₂上，过点A、B两点分别作直线l₁的垂线，垂足分别为A₁、B₁ ，我们把线段A₁B₁叫做线段AB在直线l₂上的正投影，其长度可记作T_（_AB_，_CD_）或T_（_AB_，_l₂_），特别地，线段AC在直线l₂上的正投影就是线段A₁C，请依据上述定义解决如下问题.
（1）如图1，在锐角△ABC中，AB=5，T_（_AC_，_AB_）=3，则T_（_BC_，_AB_）= ；
（2）如图2，在Rt△ABC中，∠ACB=90°，T_（_AC_，_AB_）=4，T_（_BC_，_AB_）=9，求△ABC的面积；
（3）如图3，在钝角△ABC中，∠A=60°，点D在AB边上，∠ACD=90°，T_（_AD_，_AC_）=2，T_（_BC_，_AB_）=6，求T_（_BC_，_CD_）.

查看试题解析