广东省揭阳市榕城区2023-2024学年八年级下学期数学期中考试试卷

试卷更新日期：2024-05-29 类型：期中考试

进入出卷网下载

一、选择题（本大题10小题，每小题3分，共30分）

1. 下列用数学家名字命名的图形中既是中心对称图形，又是轴对称图形的是（）

A、赵爽弦图 B、笛卡尔心形线 C、科克曲线 D、斐波那契螺旋线

查看试题解析
2. 若 $a < b$ ，则下列变形正确的是（）

A、 $2 a < 3 b$ B、 $\frac{a}{3} > \frac{b}{3}$ C、 $a - 3 < b - 3$ D、 $3 - a < 3 - b$

查看试题解析
3. 牛顿曾说过：“反证法是数学家最精良的武器之一”那么我们用反证法证明：“在一个三角形中，至少有一个内角小于或等于 $60 °$ ”时，第一步先假设（）

A、三角形中有一个内角小于 $60 °$ B、三角形中有一个内角大于 $60 °$ C、三角形中没有一个内角小于 $60 °$ D、三角形中每个内角都大于 $60 °$

查看试题解析
4. 在平面直角坐标系中，把点 $A (- 1, - 3)$ 向下平移3个单位，所得点的坐标是（）

A、 $(2, - 3)$ B、 $(- 4, - 3)$ C、 $(- 1, 0)$ D、 $(- 1, - 6)$

查看试题解析
5. 把不等式组 ${\begin{array}{l} x \leq 2 \\ x > - 1 \end{array}$ 的解集表示在数轴上，正确的是（）

A、 B、 C、 D、

查看试题解析
6. 如图，在 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 24 °$ ，延长 $B C$ 到点 $D$ ，使 $C D = A C$ ，连接 $A D$ ，则 $∠ D$ 的度数是（）

A、 $39 °$ B、 $40 °$ C、 $49 °$ D、 $51 °$

查看试题解析
7. 如图，将△ABC绕点A顺时针旋转角α（0°＜α＜180°），得到△AED ，若AC＝1，CE＝ $\sqrt{2}$ ，则α的度数为（）

A、30° B、45° C、60° D、90°

查看试题解析
8. 如图，在 $R t △ A B C$ 中， $∠ A B C = 90 °$ ， $E D$ 是 $A C$ 的垂直平分线，交 $A C$ 于点 $D$ ，交 $B C$ 于点 $E$ ， $∠ B A E = 10 °$ ，则 $∠ C$ 的度数是（）

A、 $30 °$ B、 $40 °$ C、 $45 °$ D、 $50 °$

查看试题解析
9. 若方程组 ${\begin{array}{l} 3 x + y = k + 1 \\ x + 3 y = 3 \end{array}$ 的解为 $x 、 y$ ，且 $x + y > 0$ ，则 $k$ 的取值范围是（）

A、 $k > - 4$ B、 $k > 4$ C、 $k < 4$ D、 $k < - 4$

查看试题解析
10. 如图， $A D$ 是 $△ A B C$ 的角平分线， $D F ⊥ A B$ ，垂足为 $F$ ， $D E = D G$ ， $△ A D G$ 和 $△ A E D$ 的面积分别为50和39，则 $△ E D F$ 的面积为（）

A、3.5 B、5.5 C、7 D、11

查看试题解析

二、填空题：（本大题共6个小题，每小题3分，共18分）

11. 边长为2的等边三角形的面积为

查看试题解析
12. 如果点 $P (m ， 1 + 2 m)$ 在第三象限内，那么 $m$ 的取值范围是．

查看试题解析
13. 如图，点 $A$ 的坐标为 $(1, 3)$ ，点 $B$ 在 $x$ 轴上，把 $△ O A B$ 沿 $x$ 轴向右平移到 $△ E C D$ ，若四边形 $A B D C$ 的面积为9，则点 $C$ 的坐标为．

查看试题解析
14. 某商品进价4元，标价5元出售，商家准备打折销售，但其利润率不能少于10%，则最多可打折．

查看试题解析
15. 如图，在△ABC中，BI，CI分别平分∠ABC，∠ACF，直线DE过点I，且DE∥BC，BD＝8 cm，CE＝5 cm，则DE＝．

查看试题解析
16. 数形结合是解决数学问题常用的思想方法．如图一次函数 $y = k x + b$ （ $k, b$ 为常数，且 $k < 0$ ）的图象与直线 $y = \frac{1}{3} x$ 都经过点 $A (3, 1)$ ，当 $k x + b < \frac{1}{3} x$ 时，根据图象可知， $x$ 的取值范围是．

查看试题解析

三、解答题（一）：（17题4分，18题4分，19题6分，20题6分，共20分）

17. 解不等式组 ${\begin{array}{l} 2 x - 4 > 3 (x - 2) \\ 4 x > \frac{x - 7}{2} \end{array}$ ．

查看试题解析
18. 如图， $△ A B C$ 中， $∠ A C B = 90 °$ ， $C D$ 是 $△ A B C$ 的高， $∠ A = 30 °$ ， $A B = 4$ ，求 $B D$ 的长．

查看试题解析
19. 对于任意实数 $m 、 n$ ，定义一种运算 $m ※ n = m n - m - n + 3$ ，等式的右边是通常的加减和乘法运算．例如： $3 ※ 5 = 3 \times 5 - 3 - 5 + 3 = 10$ ．请根据上述定义解决问题：若 $a < 2 ※ x < 7$ ，且解集中有两个整数解，求 $a$ 的取值范围．

查看试题解析
20. 已知线段 $M N$ 和 $∠ A C B$ ，求作一点 $P$ ，使 $P$ 到点 $M 、 N$ 的距离相等，且到 $∠ A C B$ 的两边的距离相等．（不写作法，只保留作图痕迹）

查看试题解析

四、解答题（二）：（21题8分，22题10分，23题10分，共28分）

21. 如图，把一个直角三角形ACB（∠ACB=90°）绕着顶点B顺时针旋转60°，使得点C旋转到AB边上的一点D，点A旋转到点E的位置.F，G分别是BD，BE上的点，BF=BG，延长CF与DG交于点H.

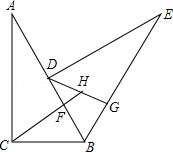(1)、求证：CF=DG；

(2)、求出∠FHG的度数.

查看试题解析
22. 如图，在平面直角坐标系中， $△ A B C$ 三个顶点的坐标分别为 $A (0, 3), B (- 3, 5), C (- 4, 1)$ ．

(1)、把 $△ A B C$ 向右平移3个单位得 $△ A_{1} B_{1} C_{1}$ ，请画出 $△ A_{1} B_{1} C_{1}$ 并写出点 $A_{1}$ 的坐标；

(2)、把 $△ A B C$ 绕原点 $O$ 旋转 $180 °$ 得到 $△ A_{2} B_{2} C_{2}$ ，请画出 $△ A_{2} B_{2} C_{2}$ ．

查看试题解析
23. 我们把符号“ $| \begin{array}{l} a & b \\ c & d \end{array} |$ ”称为二阶行列式，规定它的运算法则为 $| \begin{array}{l} a & b \\ c & d \end{array} | = a d - b c$ ，如 $| \begin{array}{l} 2 & 3 \\ 4 & 5 \end{array} | = 2 \times 5 - 3 \times 4 = - 2$ ．

(1)、求不等式 $| \begin{array}{l} 2 & 3 - x \\ 1 & x \end{array} | > 0$ 的解集．

(2)、若关于 $x$ 的不等式 $| \begin{array}{l} m & x \\ 4 & 3 \end{array} | < 0$ 的解集与（1）中的不等式解集相同，求 $m$ 的值．

(3)、若关于 $x$ 的不等式 $| \begin{array}{l} n & x \\ 2 & 1 \end{array} | < 0$ 的解都是（1）中的不等式的解，求 $n$ 的取值范围．

查看试题解析

五、解答题（三）：（本大题共2个小题，每小题12分，共24分）

24. 某商店销售10台A型和20台B型电脑的利润为4000元，销售20台A型和10台B型电脑的利润为3500元．

(1)、求每台A型电脑和B型电脑的销售利润；

(2)、该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
①求y关于x的函数关系式；
②该商店购进A型、B型电脑各多少台，才能使销售总利润最大？

查看试题解析
25. 如图，已知△ABC中，∠B=90°，AB=8cm，BC=6cm，P、Q是△ABC边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为t秒．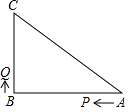

(1)、当t=2秒时，求PQ的长；

(2)、求出发时间为几秒时，△PQB是等腰三角形？

(3)、若Q沿B→C→A方向运动，则当点Q在边CA上运动时，求能使△BCQ成为等腰三角形的运动时间．

查看试题解析