广东省阳江市江城区2023-2024学年八年级下学期数学期中试题

试卷更新日期：2024-05-29 类型：期中考试

进入出卷网下载

一、选择题：本大题共10小题，每小题3分，共30分．在每小题列出的四个选项中，只有一项是符合题目要求的．

1. 二次根式 $\sqrt{x - 3}$ 中 $x$ 的取值可以是（）

A、0 B、1 C、2 D、3

查看试题解析
2. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{4}$ B、 $\sqrt{6}$ C、 $\sqrt{0.1}$ D、 $\sqrt{\frac{1}{2}}$

查看试题解析
3. 下列各组数中，是勾股数的是（）

A、 $1, \sqrt{3}, 2$ B、 $0.3, 0.4, 0.5$ C、 $5, 6, 8$ D、 $9, 12, 15$

查看试题解析
4. 下列计算正确的是（）

A、 $2 \sqrt{3} + 3 \sqrt{2} = 5 \sqrt{5}$ B、 $2 \sqrt{2} - \sqrt{2} = 1$ C、 $\sqrt{27} \div 3 = \sqrt{3}$ D、 ${(3 \sqrt{2})}^{2} = 6$

查看试题解析
5. 下列条件中，能判定四边形是平行四边形的是（）

A、一组对边相等，另一组对边平行 B、一组对边平行，一组对角相等 C、对角线相等 D、对角线互相垂直

查看试题解析
6. 若 $\sqrt{2} \times \sqrt{\frac{6}{x}}$ 是整数，则整数 $x$ 的值是（）

A、1或3 B、3或6 C、3或12 D、6或12

查看试题解析
7. 如题图，在矩形 $A B C D$ 中， $A O = 13, C D = 10$ ，则 $A D =$ （）

A、24 B、23 C、20 D、12

查看试题解析
8. 下列命题的逆命题成立的是（）

A、正方形的四个内角都是直角 B、矩形的对角线相等 C、对角线互相平分的四边形是平行四边形 D、若 $a = b$ ，则 $\sqrt{a^{2}} = \sqrt{b^{2}}$

查看试题解析
9. 如题图，四边形 $A B C D$ 是菱形， $A C = 8, D B = 6, D H ⊥ A B$ 于点 $H$ ，则 $D H$ 等于（）

A、 $\frac{24}{5}$ B、 $\frac{18}{5}$ C、 $\frac{12}{5}$ D、 $\frac{7}{5}$

查看试题解析
10. 如题图，正方形 $A B C D$ 中，点 $E$ 在 $A B$ 上，且 $A E : E B = 3 : 1$ ，点 $F$ 是 $B C$ 的中点，点 $G$ 是 $D E$ 的中点，延长 $D F$ ，与 $A B$ 的延长线交于点 $H$ ．以下四个结论：① $F G = \frac{1}{2} E H$ ；② $△ D F E$ 是直角三角形；③ $D E = E H$ ；④ $E B + C D = D E$ ．其中正确结论的个数（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题：本大题共6小题，每小题3分，共18分．请将下列各题的正确答案填写在答题卡相应的位置上．

11. 比较大小： $3 \sqrt{5}$ 7（选填“>”、“=”、“<"）．

查看试题解析
12. 最简二次根式 $\sqrt{m + 1}$ 与 $2 \sqrt{3}$ 可以合并，则 $m =$ ．

查看试题解析
13. 已知一个直角三角形的两边长分别为3和4，则第三边长为．

查看试题解析
14. 如题图，在Rt $△ A B C$ 中， $∠ A C B = 9 0^{∘}$ ，点 $D, E$ 分别是 $A B, A C$ 的中点，点 $F$ 是 $A D$ 的中点．若 $A B = 10$ ，则 $E F =$ ．

查看试题解析
15. 如题图，每个小正方形的边长为1， $A 、 B 、 C$ 是小正方形的顶点，则 $∠ A B C$ 的度数为．

查看试题解析
16. 如题图，已知正方形 $A B C D$ 的边长为2， $E$ 为 $B C$ 的中点， $D F = \frac{1}{2} C F$ ，求阴影部分的面积．

查看试题解析

三、解答题：本大题共9小题，共72分．解答应写出文字说明、证明过程或演算步骤．

17. 计算： $\sqrt{18} - 3 (\sqrt{2} - \sqrt{\frac{1}{3}})$ ．

查看试题解析
18. 如图，直线 $A O ⊥ O B$ ，垂足为 $O$ ，线段 $A O = 6, B O = 8$ ，以点 $A$ 为圆心， $A B$ 的长为半径画弧，交直线 $A O$ 于点 $C$ ．求 $O C$ 的长．

查看试题解析
19. 如图，平行四边形ABCD的对角线AC、BD相交于点O，点E、F分别为OD、OB的中点，连接CE、AF．求证：CE＝AF．

查看试题解析
20. 已知 $a = \sqrt{7} + 1, b = \sqrt{7} - 1$ ，求 $a^{2} + b^{2}$ 的值．

查看试题解析
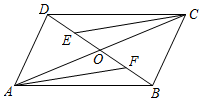21. 如图所示，某公路一侧有 $A 、 B$ 两个送奶站， $C$ 为公路上一供奶站， $C A$ 和 $C B$ 为供奶路线，现已测得 $A C = 5 k m, B C = 12 k m, A B = 13 k m, ∠ 1 = 3 0^{∘}$ ，若有一人从 $C$ 处出发，沿公路边向右行走，速度为 $3 k m / h$ ，问：多长时间后这个人距 $B$ 送奶站最近？

查看试题解析
22. 如图，矩形 $A B C D$ 沿着直线 $E F$ 对折，点 $D$ 恰好落与 $B C$ 边上的点 $H$ 重合， $H C = 16$ ， $A B = 8$ ．

(1)、判断 $△ E F H$ 的形状，并说明理由；

(2)、求 $△ E F H$ 的面积．

查看试题解析
23. 如图，在四边形 $A B C D$ 中， $A B ⊥ B D, A D / / B C, B C = \frac{1}{2} A D, E$ 为 $A D$ 的中点，连接 $B D, B E$ ．

(1)、求证：四边形 $B C D E$ 为菱形．

(2)、连接 $A C$ ，若 $A C ⊥ B E, B C = 4$ ，求 $B D$ 的长．

查看试题解析
24. 在数学课外学习活动中，小光和他的同学遇到一道题：
已知 $a = \frac{1}{2 + \sqrt{3}}$ ，求 $2 a^{2} - 8 a + 1$ 的值．他是这样解答的：
$∵ a = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}$ ， $∴ a - 2 = - \sqrt{3}$ ，
$∴ {(a - 2)}^{2} = 3, a^{2} - 4 a + 4 = 3$ ． $∴ a^{2} - 4 a = - 1$ ．
$∴ 2 a^{2} - 8 a + 1 = 2 (a^{2} - 4 a) + 1 = 2 \times (- 1) + 1 = - 1$ ．
请你根据小光的解题过程，解决如下问题：

(1)、 $\frac{1}{\sqrt{2} + 1} =$ ；

(2)、化简 $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + ⋯ + \frac{1}{\sqrt{225} + \sqrt{224}}$ ；

(3)、若 $a = \frac{1}{\sqrt{10} + 3}$ ，求 $a^{4} + 6 a^{3} + 6 a + 2023$ 的值．

查看试题解析
25.

(1)、问题情境：
数学活动课上，小明向同学们提出了这样一个问题：如图（1），在矩形 $A B C D$ 中， $A B = 2 B C, M 、 N$ 分别是 $A B, C D$ 的中点，作射线 $M N$ ，连接 $M D, M C$ ，请直接写出线段 $M D$ 与 $M C$ 之间的数量关系；

(2)、解决问题：
小亮受此问题启发，将矩形 $A B C D$ 变为平行四边形，其中 $∠ A$ 为锐角，如图（2）， $A B = 2 B C, M, N$ 分别是 $A B, C D$ 的中点，过点 $C$ 作 $C E ⊥ A D$ 交射线 $A D$ 于点 $E$ ，交射线 $M N$ 于点 $F$ ，连接 $M E, M C$ ，则 $M E = M C$ ，请你证明小亮的结论；

(3)、拓展探究：
小宇在小亮结论的基础上进行了探究，并提出了一个新问题： $∠ B M E$ 与 $∠ A E M$ 有怎样的数量关系？请你回答小宇提出的这个问题，并证明你的结论．

查看试题解析