2024年广东省深圳市中考数学全真模拟试卷(十)
试卷更新日期:2024-05-29 类型:中考模拟
一、选择题(本题共10小题,每小题3分,共30,每题有4个选项,只有一个正确选项)
-
1. 今年1月3日,我国的嫦娥四号探测器成功在月球背面着陆,标志着我国已经成功开始了对月球背面的研究,填补了国际空白.月球距离地球的平均距离为38.4万千米,数据38.4万用科学记数法表示为( )A、 B、 C、 D、2. 下列计算正确的是( )A、 B、 C、 D、3. 若a+b=3,则a2-b2+6b的值为( )A、3 B、6 C、9 D、124. 下列计算正确的是( )A、 B、 C、 D、5. 如图是一个空心圆柱体,其主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 6. 某农场开挖一条长480米的渠道,开工后每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖x米,那么下列方程中正确的是( )A、 B、 C、 D、7. 如图,为的直径,是的切线,点是切点,连接交于点 , 连接 , 若 , 则( )
6. 某农场开挖一条长480米的渠道,开工后每天比原计划多挖20米,结果提前4天完成任务,若设原计划每天挖x米,那么下列方程中正确的是( )A、 B、 C、 D、7. 如图,为的直径,是的切线,点是切点,连接交于点 , 连接 , 若 , 则( ) A、 B、 C、 D、8. 如图,、分别是的中线和角平分线, , , 则的长为( )
A、 B、 C、 D、8. 如图,、分别是的中线和角平分线, , , 则的长为( ) A、 B、 C、 D、9. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 点是线段的中点,点是轴上的一个动点,连接 , 以为直角边,点为直角顶点作等腰直角 , 连接 . 则长度的最小值是( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,直线与轴交于点 , 与轴交于点 , 点是线段的中点,点是轴上的一个动点,连接 , 以为直角边,点为直角顶点作等腰直角 , 连接 . 则长度的最小值是( )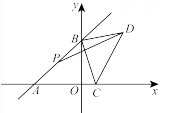 A、1 B、2 C、 D、310. 如图,点E在矩形的边上,将沿翻折,点A恰好落在边上的点F处,若 , , 则的长为( )
A、1 B、2 C、 D、310. 如图,点E在矩形的边上,将沿翻折,点A恰好落在边上的点F处,若 , , 则的长为( ) A、9 B、12 C、15 D、18
A、9 B、12 C、15 D、18二、填空题(本题共5小题,每题3分,共15分)
-
11. 分解因式:4x2-y2=.12. 如图,AB是 的直径,点P是AB延长线上的一点,PC是 的切线,C为切点,若 , ,则PC=.
 13. 如图,在第一象限内,顶点A的坐标为 , 顶点B的横坐标为2,已知反比例函数经过点B , 且与交于点C , 连接 . 若 , 则的面积为 .
13. 如图,在第一象限内,顶点A的坐标为 , 顶点B的横坐标为2,已知反比例函数经过点B , 且与交于点C , 连接 . 若 , 则的面积为 . 14. 如图,矩形的对角线和交于点 , , . 将沿着折叠,使点落在点处,连接交于点 , 交于点 , 则 .
14. 如图,矩形的对角线和交于点 , , . 将沿着折叠,使点落在点处,连接交于点 , 交于点 , 则 . 15. 两市相距150千米,甲车从 市到 市,乙车从 市到 市,两车同时出发,已知甲车速度比乙车快20千米/小时,甲车比乙车早半小时到达目的地.若设乙车的速度是 千米/小时,则根据题意,可列方程 .
15. 两市相距150千米,甲车从 市到 市,乙车从 市到 市,两车同时出发,已知甲车速度比乙车快20千米/小时,甲车比乙车早半小时到达目的地.若设乙车的速度是 千米/小时,则根据题意,可列方程 .三、解答题(本题共7小题,共55分,其中第16题6分,第17题7分,第18题、第19题、第20题、第21题8分,第22题10分)
-
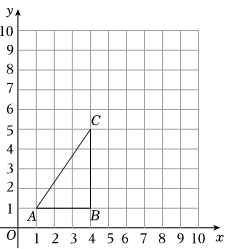
16. 计算: .17. 先化简 ,然后从 的范围内选取一个你喜欢的合适的整数作为x的值代入求值.18. 在直角坐标系中,将进行平移变换,变换前后点的坐标的情况如下表:
变换前
变换后
 (1)、平移后点的坐标是 , 并在直角坐标系中画出;(2)、若是内一点,通过上述平移变换后,点P的对应点的坐标可表示为;(3)、连接 , , 则四边形的形状是 , 其面积为 .19. 学生社团是指学生在自愿基础上结成的各种群众性文化、艺术、学术团体.不分年级、由兴趣爱好相近的同学组成,在保证学生完成学习任务和不影响学校正常教学秩序的前提下开展各种活动.某校就学生对“篮球社团、动漫社团、文学社团和摄影社团”四个社团选择意向进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整).
(1)、平移后点的坐标是 , 并在直角坐标系中画出;(2)、若是内一点,通过上述平移变换后,点P的对应点的坐标可表示为;(3)、连接 , , 则四边形的形状是 , 其面积为 .19. 学生社团是指学生在自愿基础上结成的各种群众性文化、艺术、学术团体.不分年级、由兴趣爱好相近的同学组成,在保证学生完成学习任务和不影响学校正常教学秩序的前提下开展各种活动.某校就学生对“篮球社团、动漫社团、文学社团和摄影社团”四个社团选择意向进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整).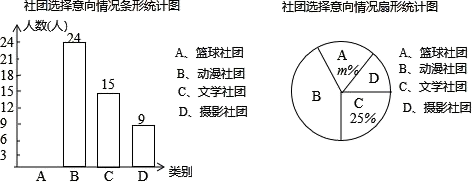
请根据图中信息,解答下列问题:
(1)、求扇形统计图中m的值,并补全条形统计图;(2)、在“动漫社团”活动中,甲、乙、丙、丁、戊五名同学表现优秀,现决定从这五名同学中任选两名参加“中学生原创动漫大赛”,恰好选中甲、乙两位同学的概率为.(3)、已知该校有1200名学生,请估计“文学社团”共有多少人?20. 如图,AB是半圆O的直径,过点O作弦AD的垂线交切线AC于点C,OC与半圆O交于点E,连接BE,DE.(1)求证:∠BED=∠C;
(2)若OA=5,AD=8,求AC的长.


