初中数学同步训练必刷培优卷(北师大版七年级下册 5.1轴对称现象)
试卷更新日期:2024-05-28 类型:同步测试
一、选择题
-
1. 川剧是汉族戏曲剧种之一,流行于四川东中部、重庆及贵州、云南部分地区.在丰富的川剧表现元素中,川剧脸谱是川剧展现给观众的最直观的视觉形象,也是人们区别川剧和其他剧种的一个重要标志.下面四幅川剧脸谱中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. (唐)元稹《长庆集》十五《景中秋)》诗:“帘断萤火入,窗明蝙蝠飞.”蝙蝠简称“蝠”,因“蝠”与“福”谐音,人们以蝠表示福气,福禄寿喜等祥瑞.下列蝙蝠纹样图中,不是轴对称图形的是( )A、
2. (唐)元稹《长庆集》十五《景中秋)》诗:“帘断萤火入,窗明蝙蝠飞.”蝙蝠简称“蝠”,因“蝠”与“福”谐音,人们以蝠表示福气,福禄寿喜等祥瑞.下列蝙蝠纹样图中,不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 3. 把26个英文字母按规律分成5组,现在还有5个字母D、M、Q、X、Z,请你按原规律补上,其顺序依次为( )
3. 把26个英文字母按规律分成5组,现在还有5个字母D、M、Q、X、Z,请你按原规律补上,其顺序依次为( )①F,R,P,J,L,G,( )
②H,I,O,( )
③N,S,( )
④B,C,K,E,( )
⑤V,A,T,Y,W,U,( )
A、Q,X,Z,M,D B、D,M,Q,Z,X C、Z,X,M,D,Q D、Q,X,Z,D,M4. 如图,在的正方形网格中,图中的为格点三角形,在图中与成轴对称的格点三角形最多可以找出( ) A、6个 B、5个 C、4个 D、3个5. 下列判断中,正确的是( )A、直角三角形一定不是轴对称图形 B、角是轴对称图形,角平分线是它的对称轴 C、线段是轴对称图形,它的对称轴是过该线段中点的任意一条直线 D、等边三角形是轴对称图形,它有三条对称轴6. 在如图所示的图形中,不是轴对称图形的是( )A、
A、6个 B、5个 C、4个 D、3个5. 下列判断中,正确的是( )A、直角三角形一定不是轴对称图形 B、角是轴对称图形,角平分线是它的对称轴 C、线段是轴对称图形,它的对称轴是过该线段中点的任意一条直线 D、等边三角形是轴对称图形,它有三条对称轴6. 在如图所示的图形中,不是轴对称图形的是( )A、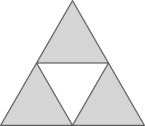 B、
B、 C、
C、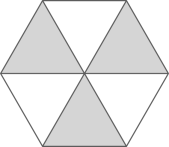 D、
D、 7. 下列描述的图形不一定是轴对称图形的是( )A、90°的角 B、含有80°,80°两角的三角形 C、含有150°,15°两角的三角形 D、含有60°角的三角形.8. 如图,图中的阴影部分是由5个小正方形组成的一个图形,若在图中的方格里再涂黑一个正方形,使整个阴影部分成为轴对称图形,涂法有( )
7. 下列描述的图形不一定是轴对称图形的是( )A、90°的角 B、含有80°,80°两角的三角形 C、含有150°,15°两角的三角形 D、含有60°角的三角形.8. 如图,图中的阴影部分是由5个小正方形组成的一个图形,若在图中的方格里再涂黑一个正方形,使整个阴影部分成为轴对称图形,涂法有( ) A、3种 B、4种 C、5种 D、6种
A、3种 B、4种 C、5种 D、6种二、填空题
-
9.
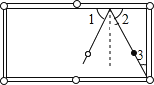
数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于 .
 10.
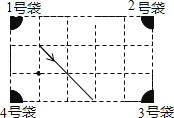
10.如图是一个经过改造的台球桌面的示意图,图中四个角上的黑色部分分别表示四个入球孔.如果一个球按图中所示的方向被击出(球可以经过多次反弹),那么该球最后将落入的球袋是号袋(填球袋的编号).
 11. 如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且以格占为顶点的三角形,这样的三角形共有个,请在下面所给的格纸中一一画出。(所给的六个格纸未必全用)。
11. 如图,在2×2的正方形格纸中,有一个以格点为顶点的△ABC,请你找出格纸中所有与△ABC成轴对称且以格占为顶点的三角形,这样的三角形共有个,请在下面所给的格纸中一一画出。(所给的六个格纸未必全用)。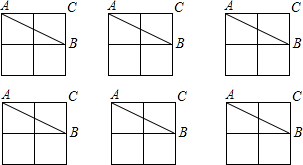 12.
12.在4×4的正方形网格中,已将图中的四个小正方形涂上阴影(如图),若再从其余小正方形中任选一个也涂上阴影,使得整个阴影部分组成的图形成轴对称图形.那么符合条件的小正方形共有 个.

三、解答题
-
13.
请你用3种方法,将如图所示的四块小正方形纸板拼成一个大的正方形,并且使拼成的大正方形是至少有两条对称轴的轴对称图案.
 14. 两个大小不同的圆在同平面内可以组成下图的五组图形,请画出每组图形的对称轴,并说一说它们的对称轴有什么共同的特点.
14. 两个大小不同的圆在同平面内可以组成下图的五组图形,请画出每组图形的对称轴,并说一说它们的对称轴有什么共同的特点. 15.
15.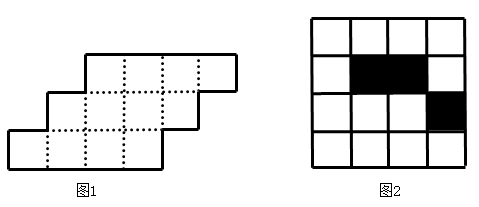 (1)、请你沿着图1中的虚线,用两种方法将图1划分为两个全等的图形;(2)、如图2,是 的正方形网格,其中已有3个小方格涂成了阴影,请你从其余的13个白色的小方格中选出一个也涂成阴影,使整个涂成阴影的图形成为轴对称图形.请用三种方法在图中补全图形,并画出它们各自的对称轴(所画的三个图形不能全等)16. 为了美化环境,在一块正方形空地上分别种植四种不同的花草.现将这块空地按下列要求分成四块:
(1)、请你沿着图1中的虚线,用两种方法将图1划分为两个全等的图形;(2)、如图2,是 的正方形网格,其中已有3个小方格涂成了阴影,请你从其余的13个白色的小方格中选出一个也涂成阴影,使整个涂成阴影的图形成为轴对称图形.请用三种方法在图中补全图形,并画出它们各自的对称轴(所画的三个图形不能全等)16. 为了美化环境,在一块正方形空地上分别种植四种不同的花草.现将这块空地按下列要求分成四块:
⑴分割后的整个图形必须是轴对称图形;
⑵四块图形形状相同;
⑶四块图形面积相等.
现已有两种不同的分法:
(1)、分别作两条对角线(如图中的图(1));(2)、过一条边的四等分点作这边的垂线段(图(2))(图(2)中两个图形的分割看作同一方法).请你按照上述三个要求,分别在图(3)、图(4)两个正方形中画出另外两种不同的分割方法.(符合题意画图,不写画法)

