2024年广东省深圳市中考数学全真模拟试卷(九)

试卷更新日期：2024-05-28 类型：中考模拟

进入出卷网下载

一、选择题(本题共10小题，每小题3分，共30分，每小题有4个选项，只有一个正确选项)

1. 下列运算正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $a^{2} + 3 a = 4 a^{3}$ C、 ${(- 2 a^{2} b)}^{3} = - 8 a^{6} b^{3}$ D、 $(a + 2) (a - 2) = a^{2} - 2$

查看试题解析
2. 将一副三角板按如图所示方式摆放，使有刻度的边互相垂直，则 $∠ 1 =$ （）

A、 $45 °$ B、 $50 °$ C、 $60 °$ D、 $75 °$

查看试题解析
3. 南宋数学家杨辉所著《田亩比类乘除算法》中记载：“直田积八百六十四步，只云阔与长共六十步，问阔及长各几步．”意思是：一块矩形田地的面积是864平方步，它的宽和长共60步，问它的宽和长各多少步？设它的宽为x步，则可列方程为（）

A、 $x \cdot (60 + x) = 864$ B、 $x \cdot (60 - 2 x) = 864$ C、 $x \cdot (30 - x) = 864$ D、 $x \cdot (60 - x) = 864$

查看试题解析
4. 据国家统计局2024年1月17日公布的数据，初步核算，2023年我国国内生产总值 $(G D P)$ 约为1260000亿元．将1260000亿元用科学记数法表示为（）

A、 $1.26 \times 10 ^{5}$ 亿元 B、 $1.26 \times 10 ^{6}$ 亿元 C、 $12.6 \times 10 ^{5}$ 亿元 D、 $126 \times 10 ^{4}$ 亿元

查看试题解析
5. 如图，等边 $△ A B C$ 中，点 $D$ ， $E$ 分别在边 $B C$ ， $A C$ 上， $B D = C E = \frac{1}{3} A B$ ， $A D, B E$ 交于点 $F$ ．若 $A B = 6$ ．则 $E F$ 的长为（）

A、 $2 \sqrt{7}$ B、 $\frac{4 \sqrt{7}}{3}$ C、 $\frac{5 \sqrt{7}}{4}$ D、 $\frac{8 \sqrt{7}}{7}$

查看试题解析
6. 一件工程，甲单独做需要a小时完成，乙单独做需要b小时完成．若甲、乙二人合作完成此项工作，需要的时间是（）

A、 $\frac{a + b}{2}$ 小时 B、 $(\frac{1}{a} + \frac{1}{b})$ 小时 C、 $\frac{1}{a + b}$ 小时 D、 $\frac{a b}{a + b}$ 小时

查看试题解析
7. 甲乙丙丁四人互相给其他三人之一写信，选择对象的方式等可能.问存在两个人收到对方的信的概率（）

A、 $\frac{2}{3}$ B、 $\frac{5}{9}$ C、 $\frac{17}{27}$ D、 $\frac{55}{81}$

查看试题解析
8. 如图1，在矩形 $A B C D$ 中， $B D = 2 A B$ ， M为 $A D$ 的中点，N是线段 $B D$ 上的一动点．设 $D N = x$ ， $M N + A N = y$ ，图2是y关于x的函数图象，其中Q是图象上的最低点，则a的值为（）

A、6 B、8 C、5 D、 $\sqrt{35}$

查看试题解析
9. 如图，等边 $△ A B C$ 的边长为6，D是 $B C$ 的中点，E是 $A C$ 边上的一点，连接 $D E$ ，以 $D E$ 为边作等边 $△ D E F$ ，若 $C E = 2$ ，则线段 $A F$ 的长为（）

A、 $\sqrt{7}$ B、 $\frac{7}{2}$ C、 $\frac{7}{3}$ D、 $2 \sqrt{2}$

查看试题解析

二、填空题(本题共5小题，每小题3分，共15分)

10. 分解因式： $3 a - 3 a b^{2} =$ .

查看试题解析
11. 如图， $∠ A E C = 80 °$ ，在 $∠ A E C$ 的两边上分别过点A和点C向同方向作射线 $A B$ 和 $C D$ ，且 $A B ∥ C D$ ，若 $∠ E A B$ 和 $∠ E C D$ 的角平分线所在的直线交于点P（P与C不重合），则 $∠ A P C$ 的大小为．

查看试题解析
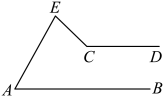12. 如图，在矩形ABCD中， $AD = 5$ ， $AB = 8$ ，点E为射线DC上一个动点，把 $△ ADE$ 沿直线AE折叠，当点D的对应点F刚好落在线段AB的垂直平分线上时，则DE的长为．

查看试题解析
13. 如图，直线 $y = - \frac{1}{2} x + 2$ 与x轴，y轴交于A、B两点，C为双曲线 $y = \frac{k}{x} (x > 0)$ 上一点，连接 $A C$ 、 $B C$ ，且 $B C$ 交x轴于点M ， $\frac{B M}{C M} = \frac{3}{4}$ ，若 $△ A B C$ 的面积为 $\frac{19}{3}$ ，则k的值为．

查看试题解析
14. 如图，在菱形 $A B C D$ 中，E、F分别是 $A B$ ， $B C$ 边上的中点， $G$ 为 $D E$ 上一点，若 $A B = 4$ ， $∠ B = ∠ E G F = 60 °$ ，则 $D G$ 的长为

查看试题解析

三、解答题(本题共7小题，共55分，其中16题6分，第17题7分，第18、19、20题8分，第21题9分)，第22题10分

15. 计算： $(- 3)^{4} \div [2 - (- 7)] + 6 \times (\frac{1}{2} - 1)$

查看试题解析
16. 先化简，再求值： $\frac{x^{2} - 6 x + 9}{x + 2} \div \frac{x^{2} - 3 x}{x + 2} - \frac{3}{x}$ ，其中 $x = \sqrt{3}$ ．

查看试题解析
17. 学校七年级的学生对老年人处理生病问题的方式进行了调查： $A$ ．子女陪同去医院就诊； $B$ ．独自去医院就诊； $C$ ．自己在家里服用备用药； $D$ ．请人帮忙购药； $E$ ．其它．发出60份问卷全部收回，均为有效问卷，将调查结果整理如下：
方式
$A$
$B$
$C$
$D$
$E$
人数
6
18
24
9
3

(1)、补全条形统计图；

(2)、画出扇形统计图．

查看试题解析
18. 如图，在每个小正方形的边长为1的网格中， $A$ ， $B$ ， $C$ 为格点， $D$ 为小正方形边的中点.

(1)、 $A C$ 的长等于；

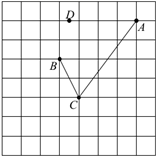(2)、点 $P$ ， $Q$ 分别为线段 $B C$ ， $A C$ 上的动点，当 $P D + P Q$ 取得最小值时，请在如图所示的网格中，用无刻度的直尺，画出线段 $P D$ ， $P Q$ ，并简要说明点 $P$ 和点 $Q$ 的位置是如何找到的（不要求证明）.

查看试题解析
19. 某蔬菜种植基地为提高蔬菜产量，计划对甲、乙两种型号蔬菜大棚进行改造，根据预算，改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元，改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元．
（1）改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元？
（2）已知改造1个甲种型号大棚的时间是5天，改造1个乙种型号大概的时间是3天，该基地计划改造甲、乙两种蔬菜大棚共8个，改造资金最多能投入128万元，要求改造时间不超过35天，请问有几种改造方案？哪种方案基地投入资金最少，最少是多少？

查看试题解析
20. 筒车是我国古代利用水力驱动的灌溉工具，如图，半径为3m的筒车⊙O按逆时针方向每分钟转 $\frac{5}{6}$ 圈，筒车与水面分别交于点A、B ，筒车的轴心O距离水面的高度OC为2.2m ，筒车上均匀分布着若干个盛水筒，若以某个盛水筒P刚浮出水面（点A）时开始计算时间．

(1)、求盛水筒P从A点到达最高点所经过的路程；

(2)、求浮出水面3.4秒时，盛水筒P到水面的距离；

(3)、若接水槽MN所在直线是⊙O的切线，且与直线AB交于点M ， MO＝8m ，直接写出盛水筒P从最高点开始，经过多长时间恰好第一次落在直线MN上．（参考数据：cos43°＝sin47°≈ $\frac{11}{15}$ ， sin16°＝cos74°≈ $\frac{11}{40}$ ， sin22°＝cos68°≈ $\frac{3}{8}$ ）

查看试题解析
21. 综合与实践
问题情境：“综合实践课”上，老师画出了如图1所示的矩形 $A B C D$ ， $A D = n A B$ （其中 $n > 1$ ），P（不与点A重合）是 $A D$ 边上的动点，连接点P与 $A B$ 边的中点E ，将 $△ A P E$ 沿直线 $P E$ 翻折得到 $△ O P E$ ，延长 $P O$ 交 $B C$ 于点F（点F不与点C重合），作 $∠ P F C$ 的平分线 $F G$ ，交矩形 $A B C D$ 的边于点G ．问 $P E$ 与 $F G$ 的位置关系？

(1)、数学思考：
请你解答老师提出的问题，并说明理由．

(2)、深入探究：
老师将图1中的图形通过几何画板改动为如图2，在点P运动过程中，连接 $E G$ ，若E ， O ， G三点共线，点G与点D刚好重合，求n的值．

(3)、若 $n = 2$ ，连接 $P G, O G$ ，当 $△ P O G$ 是以 $O P$ 为直角边的直角三角形，且点G落在 $A D$ 边上时，请直接写出 $\frac{D P}{A P}$ 的值．

查看试题解析

方式	$A$	$B$	$C$	$D$	$E$
人数	6	18	24	9	3