河北省张家口市桥西区2023-2024学年八年级下学期数学期中试题

试卷更新日期：2024-05-28 类型：期中考试

进入出卷网下载

一、选择题（本大题共12个小题，每题3分，共36分。在每小题给出的四个选项中，只有一项是符合题目要求的）

1. 下列各式中，是分式的是（）

A、 $\frac{1}{2}$ B、 $\frac{b}{2}$ C、 $\frac{b}{2 a}$ D、 $\frac{a}{π}$

查看试题解析
2. 下列图形中，不是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 下列从左到右的变形中是因式分解的有（）
① $(a + 3) (a - 3) = a^{2} - 9$ ； ② $m^{2} - 4 = (m + 2) (m - 2)$ ；
③ $a^{2} - b^{2} + 1 = (a + b) (a - b) + 1$ ； ④ $2 m R + 2 m r = 2 m (R + r)$ ．

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 在平面直角坐标系中，点 $A (4, - 2)$ 向下平移5个单位长度后，得到对应点的坐标为（）

A、 $(4, - 7)$ B、 $(4, 3)$ C、 $(- 1, - 2)$ D、 $(9, - 2)$

查看试题解析
5. 等腰 $△ A B C$ 中， $A B = A C$ ， $∠ B = 72 °$ ，则 $∠ A$ 的度数为（）

A、 $30 °$ B、 $36 °$ C、 $45 °$ D、 $72 °$

查看试题解析
6. 甲、乙两地相距 $1400 k m$ ，乘高铁列车从甲地到乙地比乘特快列车少用 $9 h$ ，已知高铁列车的平均行驶速度是特快列车的2.8倍，根据题意可列方程， $\frac{1400}{x} - \frac{1400}{2.8 x} = 9$ ，则方程中 $x$ 表示（）

A、特快列车的平均行驶速度 B、高铁列车的平均行驶速度 C、特快列车的行驶时间 D、高铁列车的行驶时间

查看试题解析
7. 如图所示的 $R t △ A B C$ 向右翻滚，下列说法正确的有（）
1）① $\Rightarrow$ ②是旋转；
2）① $\Rightarrow$ ③是平移；
3）① $\Rightarrow$ ④是平移；
4）② $\Rightarrow$ ③是旋转．

A、1种 B、2种 C、3种 D、4种

查看试题解析
8. 计算： $10 5^{2} - 10 \times 105 + 5^{2} =$ （）

A、100 B、110 C、1210 D、10000

查看试题解析
9. 如图在△ABC中，边AB，AC的垂直平分线交于点P，连结BP，CP，若∠A=50°，则∠BPC=（）

A、100° B、95° C、90° D、50°

查看试题解析
10. 分式 $\frac{x + a}{2 x - 1}$ 中，当 $x = - a$ 时，下列结论正确的是（）

A、分式的值为零 B、分式无意义 C、若 $a \neq \frac{1}{2}$ 时，分式的值为零 D、若 $a \neq - \frac{1}{2}$ 时，分式的值为零

查看试题解析
11. 在 $△ A B C$ 中， $∠ B = 60 °$ ， $A B = 2$ ，若 $△ A B C$ 是锐角三角形，则满足条件的 $B C$ 长可以是（）

A、1 B、2 C、4 D、5

查看试题解析
12. 若关于 $x$ 的方程 $\frac{x - a}{x - 1} - \frac{3}{x} = 1$ 的解为整数，则整数 $a$ 的值的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

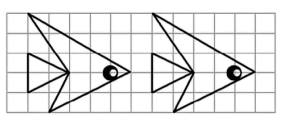
13. 多项式 $2 x^{2} + 6 x^{3}$ 中各项的公因式是．

查看试题解析
14. 在边长为1的正方形网格中，右边的“小鱼”图案是由左边的图案经过一次平移得到的，则平移的距离是．

查看试题解析
15. 若关于 $x$ 的分式方程 $\frac{1}{x - 2} = 1 - \frac{m}{2 - x}$ 无解，则 $m =$ ．

查看试题解析
16. 如图，在四边形ABCD中，∠ABC=90°，AB=3，BC=4，CD=5，DA=5 $\sqrt{2}$ ，则BD的长为．

查看试题解析

三、解答题（本大题共8个小题，共52分，解答应写出文字说明、证明过程或演算步骤）

17. 如图，卡片A、B、C各代表一个代数式，从三张卡片中取两张进行因式分解运算．

(1)、若选择B、C卡片，请进行因式分解；

(2)、嘉嘉发现：“若选择A、B卡片，不论 $k$ 为何整数，其结果总可以被 $m (m \neq 1)$ 整除”，请确定满足条件的最小正整数 $m$ 的值．

查看试题解析
18. 如图，在 $2 \times 4$ 的方格纸 $A B C D$ 中，每个小方格的边长为1，已知格点 $P$ ．

(1)、在方格纸中画一个格点三角形（顶点均在格点上），使 $∠ P = ∠ Q = 45 °$ ，点 $Q$ 在 $B C$ 上，点 $R$ 在 $A D$ 上；

(2)、将（1）中的 $△ P Q R$ 向右平移1个单位，得到 $△ P^{'} Q^{'} R^{'}$ ，画出 $△ P^{'} Q^{'} R^{'}$ ；设 $△ P Q R$ 扫过的最大面积为 $S$ ，直接写出 $S$ 的值．

查看试题解析
19. 老师设计了接力游戏，用合作的方式完成分式化简，规则是每人只能看到前一人给的式子，并进一步计算，再将结果传递给下一人，最后完成化简，过程如图所示：
但老师最后说，结果是错的，请你确定接力中出错的同学，并写出正确的过程．

查看试题解析

20. 下面是琪琪同学证明定理时使用的两种添加辅助线的方法，选择其中一种，完成证明．

定理：在直角三角形中，如果一个锐角等于 $30 °$ ，那么它所对的直角边等于斜边的一半．

已知：如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $∠ A = 30 °$ ．

求证： $B C = \frac{1}{2} A B$ ．

方法一

证明：如图，延长 $B C$ 至点 $D$ ，使 $B D = A B$ ，连接 $A D$ ．

方法二

证明：如图，在线段 $A B$ 上取一点 $D$ ，使得 $B D = B C$ ，连接 $C D$ ．

查看试题解析

21. 某中学的校园中有两块草坪．草坪甲是边长为 $m$ 的正方形，中间有一个边长为2的正方形喷水池，草坪乙是长为 $2 m$ ，宽为 $(m - 2)$ 的长方形 $(m > 2)$ ，设两块草坪的面积分别为 $S_{甲}$ 、 $S_{乙}$ ．

(1)、比较甲、乙两块草坪面积的大小；

(2)、求甲、乙块草坪的面积的比．

查看试题解析
22. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ，将 $△ A B C$ 绕着点 $B$ 逆时针旋转得到 $△ F B E$ ，点 $C$ ， $A$ 的对应点分别为 $E$ ， $F$ ，点 $E$ 落在 $B A$ 上，连接 $A F$ ．

(1)、若 $∠ B A C = 42 °$ ．求 $∠ B A F$ 的度数；

(2)、若 $A C = 4$ ， $B C = 3$ ，求 $A F$ 的长．

查看试题解析
23. 长为 $300 m$ 的春游队伍，以 $v (m / s)$ 的速度向东行进，如图1和图2，当队伍排尾行进到位置 $O$ 时，在排尾处的甲有一物品要送到排头，送到后立即返回排尾，甲的往返速度均为 $2 v (m / s)$ ，当甲返回排尾后，他及队伍均停止行进．

(1)、求甲这次往返的时间 $t_{往}$ ， $t_{返}$ ；（用含 $v$ 的代数式表示）

(2)、求甲这次往返队伍的过程中队伍行进的路程．

查看试题解析
24. 如图， $△ A B C$ 中， $A B = A C = 4 \sqrt{3}$ ， $∠ A = 30 °$ ， $C A^{'}$ 从 $C A$ 开始绕点 $C$ 逆时针旋转 $α$ 角 $(0 ° < α < 150 °)$ ，与射线 $A B$ 相交于点 $E$ ， $∠ A C A^{'}$ 的角平分线所在的直线交射线 $A B$ 相交于点 $D$ ，连接 $A^{'} D$ ．

(1)、求证： $A^{'} D = A D$ ；

(2)、若 $△ A^{'} D E$ 为轴对称图形时，求 $α$ ；

(3)、当 $A^{'} E$ 、 $A^{'} D$ 、 $D E$ 的中垂线的交点落在 $△ A^{'} D E$ 的某一边上时，直接写出点 $D$ 到 $A C$ 的距离．

查看试题解析