河北省秦皇岛市卢龙县2023-2024学年八年级下学期数学期中试题

试卷更新日期：2024-05-28 类型：期中考试

进入出卷网下载

一、精心选一选，慧眼识金!（本大题共14小题，每小题3分，共42分，在每小题给出的四个选项中只有一项是正确的）

1. 以下调查中，最适合用来全面调查的是（）

A、了解班级每位同学穿鞋的尺码 B、了解中学生的心理健康状况 C、调查滦河水质情况 D、了解市民做高铁出行的意愿

查看试题解析
2. 某校从800名学生中随机抽取100名学生进行百米测试，下列说法正确的是（）

A、该调查方式是普查 B、每名学生的百米测试成绩是个体 C、样本容量是800 D、100名学生的百米测试成绩是总体

查看试题解析
3. 要反映卢龙某周内每天最高气温的变化情况，采用的统计图比较合适的是（）

A、条形统计图 B、扇形统计图 C、折线统计图 D、上述三种统计图都可以

查看试题解析
4. 在进行路程s ，速度v ，时间t的相关计算中，若路程s不变，则下列说法不正确的是（）

A、速度v是变量 B、速度v ，时间t都是变量 C、时间t是变量 D、路程s ，速度v ，时间t都是常量

查看试题解析
5. 下列图像不能反映y是x的函数的是（）

A、 B、 C、 D、

查看试题解析
6. 在频数分布直方图中，各个小组的频数比为1：5：4：6，则对应的小长方形的高的比为（）

A、1：4：5：3 B、1：5：3：6 C、1：5：4：6 D、6：4：5：1

查看试题解析
7. 如图，以学校为参照点，对小明家位置的描述最准确的是（）

A、距离学校1200米处 B、西南方向上的1200米处 C、南偏西65°方向上的1200米处 D、南偏西25°方向上的1200米处

查看试题解析
8. 若在象棋盘上建立直角坐标系，使“将”位于点（1，-2），“象”位于点（3，-2），则“炮”位于点（）

A、 $(1, - 1)$ B、 $(- 1, 1)$ C、 $(- 1, 2)$ D、 $(1, - 2)$

查看试题解析
9. 一次数学测试后，某班50名学生的成绩被分为5组，第1~4组的频数分别为10、10、12、13，则第5组的频率是（）

A、0.1 B、0.2 C、0.3 D、0.4

查看试题解析
10. 在平面直角坐标系中，一矩形上各点的纵坐标不变，横坐标变为原来的 $\frac{1}{2}$ ，则该矩形发生的变化为（）

A、向左平移了二个单位长度 B、向下平移了二个单位长度 C、横向压缩为原来的一半 D、纵向压缩为原来的一半

查看试题解析
11. 某校七年级开展“阳光体育”活动，对喜欢乒乓球、足球、篮球、羽毛球的学生人数进行统计（每人只能选择其中一项），得到如图所示的扇形统计图.若喜欢羽毛球的人数是喜欢足球的人数的 $4$ 倍，喜欢乒乓球的人数是 $21$ 人，则下列说法正确的是（）

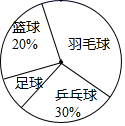A、被调查的学生人数为 $80$ 人 B、喜欢篮球的人数为 $16$ 人 C、喜欢足球的扇形的圆心角为 $36 °$ D、喜欢羽毛球的人数占被调查人数的 $35 %$

查看试题解析
12. 已知甲、乙、丙三人所处位置不同．甲说：“以我为坐标原点，乙的位置是 $(2, 3)$ ． ”丙说：“以我为坐标原点，乙的位置是 $(- 3, - 2)$ ． ”若以乙为坐标原点（三人建立平面直角坐标系时，x轴、y轴正方向分别相同），甲、丙的坐标分别是（）

A、 $(- 3, - 2)$ ， $(2, - 3)$ B、 $(- 3, 2)$ ， $(3, 2)$ C、 $(- 2, - 3)$ ， $(3, 2)$ D、 $(- 2, - 3)$ ， $(- 3, - 2)$

查看试题解析
13. 向最大容量为60升的热水器内注水，每分钟注水10升，注水2分钟后停止1分钟，然后继续注水，直至注满.则能反映注水量与注水时间函数关系的图象是（）

A、 B、 C、 D、

查看试题解析
14. 下面三个问题中都有两个变量：
①如图1，货车匀速通过隧道（隧道长大于货车长），货车在隧道内的长度y与从车头进入隧道至车尾离开隧道的时间x；
②如图2，实线是王大爷从家出发匀速散步行走的路线（圆心O表示王大爷家的位置），他离家的距离y与散步的时间x；
③如图3，往一个圆柱形空杯中匀速倒水，倒满后停止，一段时间后，再匀速倒出杯中的水，杯中水的体积y与所用时间x
其中，变量y与x之间的函数关系大致符合图4的是（）

A、①② B、①③ C、②③ D、①②③

查看试题解析

二、填空题（简洁的结果，表达的是你敏锐的思维，需要的是细心！每小题3分，共18分）

15. 剧院里1排5号可以用 $(1, 5)$ 表示，则 $(6, 2)$ 表示．

查看试题解析
16. 函数y= $\sqrt{x - 5}$ 中自变量x的取值范围是

查看试题解析
17. 若正方体的棱长为 $x$ ，表面积为 $y$ ，则 $y$ 与 $x$ 的关系式为．

查看试题解析
18. 点 $A (m - 1, 2)$ 与点 $B (3, n - 1)$ 关于y轴对称，则 ${(m + n)}^{2023}$ 的值为．

查看试题解析
19. 点 $A (a, 4)$ 在第-象限，且到y轴的距离为3，直线 $A C ∥ y$ 轴，且 $A C = 3$ ．则点C的坐标为．

查看试题解析
20. 某市地铁票价计费标准如表所示：乘车距离x（单位：公里）
乘车距离x
$x \leq 6$
$6 < x \leq 12$
$12 < x \leq 22$
$22 < x \leq 32$
$x > 32$
票价（元）
3
4
5
6
每增加1元可乘20公里
另外，使用市政交通一卡通，每个自然月每张卡片支出累计满100元后，超出部分打8折；满150元后，超出部分打5折；支出累计达400元后，不再打折．小红妈妈上班时，需要乘坐地铁15公里到达公司，每天上下班共乘坐两次，如果每次乘坐地铁都使用市政交通一卡通，那么每月第22次乘坐地铁上下班时，她刷卡支出的费用是元．

查看试题解析

三、解答题（耐心计算，认真推理，表露你萌动的智慧!共60分）

21. 如图，我们把杜甫的《绝句》整齐排列放在平面直角坐标系中．

(1)、“岭”和“船”的坐标依次是、；

(2)、将第2行与第3行对调，再将第3列与第7列对调，“雪”由开始的坐标依次变换为和；

(3)、“泊”开始的坐标是 $(2, 1)$ ，使它的坐标变换到 $(5, 3)$ ，应该哪两行对调，同时哪两列对调？

查看试题解析
22. 已知点 $P (a - 3, 2 a + 5)$ ，分别根据下列条件求出点P的坐标．

(1)、点P在x轴上；

(2)、点P在y轴上；

(3)、点P到两坐标轴的距离相等；

(4)、与点 $(4, 3)$ 的连线平行于x轴．

查看试题解析
23. 为了解我校学生对：A．航模；B．机器人；C.3D打印；D．扎染四个社团的喜爱情况，随机抽取了m名学生进行调查（要求每名学生选出并且只能选出一个自己喜爱的社团），并将调查结果绘制成如下两幅不完整的统计图．根据统计图提供的信息，回答下列问题：

(1)、 $m =$ ， $n =$ ；

(2)、扇形统计图中，喜爱航模社团所对应的扇形的圆心角度数是度；

(3)、补全条形统计图；

(4)、根据调查结果，估计我校6000名学生中，大约有多少名学生喜爱3D打印社团．

查看试题解析
24. 如图，在平面直角坐标系中，点A的坐标为 $(- 2, 2)$ ，点B与点A关于x轴对称，点B先向右平移4个单位长度，再向上平移2个单位长度得到点C ．

(1)、描出点B和点C ，并依次连接AB、BC、CA ，得到△ABC；

(2)、将（1）中的△ABC的各顶点的横坐标和纵坐标都乘 $\frac{3}{2}$ ，得到点A的对应点A ，点B的对应点 $B_{1}$ ，点C的对应点 $C_{1}$ ，在平面直角坐标系中描出点 $A_{1}$ 、 $B_{1}$ 、 $C_{1}$ ，并依次连接 $A_{1} B_{1}$ 、 $B_{1} C_{1}$ 、 $C_{1} A_{1}$ ，得到 $△ A_{1} B_{1} C_{1}$ ；

(3)、在（2）的条件下， $\frac{S_{△ A_{1} B_{1} C_{1}}}{S_{△ A B C}} =$ ．

查看试题解析
25. 如图，一列快车从甲地驶往乙地，-列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），图中的折线表示y与x之间的函数关系．根据图象进行以下探究：

(1)、甲、乙两地之间的距离为；

(2)、请解释图中点B的实际意义为；

(3)、求慢车和快车的速度分别是多少？

查看试题解析
26. 如图①，在正方形ABCD中，点P以1cm/s的速度从点A出发按箭头方向在正方形的边上运动，到达点D后停止，△PAD的面积y（cm²）与运动时间x（s）之间的函数关系如图②所示．（规定：点P在点A、D时， $y = 0$ ）

(1)、发现：
① $A B =$ cm，当 $x = 17$ 时， $y =$ ；
②当点P在线段上运动时，y的值保持不变；

(2)、拓展：求当 $0 < x < 6$ 及 $12 < x < 18$ 时，y与x之间的函数关系式．

(3)、探究：当x的值为多少时？y的值等于15．

查看试题解析

乘车距离x	$x \leq 6$	$6 < x \leq 12$	$12 < x \leq 22$	$22 < x \leq 32$	$x > 32$
票价（元）	3	4	5	6	每增加1元可乘20公里