广东省珠海市香洲区联考2023-2024学年八年级下学期数学期中试题
试卷更新日期:2024-05-28 类型:期中考试
一、选择题(本大题10小题,每小题3分,共30分)每小题给出四个选项中只有一个是正确的,请把答题卡上,对应题目所选的选项涂黑.
-
1. 下列式子中,最简二次根式是( )A、 B、 C、 D、2. 二次根式有意义的条件是( )A、x>3 B、x>-3 C、x≥-3 D、x≥33. 下列运算正确的是( )A、 B、3 C、 D、4. 如图,在中,对角线AC与BD相交于点O , 则下列结论错误的是( )
 A、AB=CD B、OB=OD C、AB=AD D、∠ABC=∠ADC5. 下列命题是假命题的是( )A、一组对边相等,一组对角相等的四边形是平行四边形 B、对角线互相平分且相等的四边形是矩形 C、对角线互相垂直平分的四边形是菱形 D、对角线相等的菱形是正方形6. 如图,直角三角形的两直角边分别是3和4,则斜边上的高BD的长是( )
A、AB=CD B、OB=OD C、AB=AD D、∠ABC=∠ADC5. 下列命题是假命题的是( )A、一组对边相等,一组对角相等的四边形是平行四边形 B、对角线互相平分且相等的四边形是矩形 C、对角线互相垂直平分的四边形是菱形 D、对角线相等的菱形是正方形6. 如图,直角三角形的两直角边分别是3和4,则斜边上的高BD的长是( ) A、1.8 B、2 C、2.4 D、2.87. 如图,在平面直角坐标系xOy中,菱形OABC的顶点C的坐标是(3,4),则B的坐标为( )
A、1.8 B、2 C、2.4 D、2.87. 如图,在平面直角坐标系xOy中,菱形OABC的顶点C的坐标是(3,4),则B的坐标为( ) A、(7,3) B、(8,4) C、(7,4) D、(6,4)8. 如图,在矩形ABCD中,两条对角线AC、BD相交于点O , 若AB=OB=5.则AC的长是( )
A、(7,3) B、(8,4) C、(7,4) D、(6,4)8. 如图,在矩形ABCD中,两条对角线AC、BD相交于点O , 若AB=OB=5.则AC的长是( ) A、10 B、8 C、 D、59. 正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积( )
A、10 B、8 C、 D、59. 正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积( )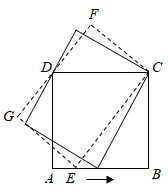 A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变10. 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E , PF⊥CD于点F , 连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=2PE . 其中有正确结论的是( )
A、先变大后变小 B、先变小后变大 C、一直变大 D、保持不变10. 如图,点P是正方形ABCD的对角线BD上一点,PE⊥BC于点E , PF⊥CD于点F , 连接EF给出下列五个结论:①AP=EF;②AP⊥EF;③△APD一定是等腰三角形;④∠PFE=∠BAP;⑤PD=2PE . 其中有正确结论的是( ) A、①②③ B、①③⑤ C、②③④ D、①②④
A、①②③ B、①③⑤ C、②③④ D、①②④二、填空题(本大题8小题,每小题3分,共24分)请将下列各题的正确答案填写在答题卡相应的位置上.
-
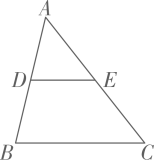
11. 化简 .12. 如图,在中,点D、E分别是边、的中点, , 则 .
 13. 直角三角形两直角边长分别为5和12,则它斜边上的中线长为 .14. 如图,平行四边形ABCD中,BE平分∠ABC交AD于E点,已知AB=4,AD=5,则DE长为 .
13. 直角三角形两直角边长分别为5和12,则它斜边上的中线长为 .14. 如图,平行四边形ABCD中,BE平分∠ABC交AD于E点,已知AB=4,AD=5,则DE长为 . 15. 如图,菱形的对角线 , 相交于点O , 若 , , 则菱形的面积为 .
15. 如图,菱形的对角线 , 相交于点O , 若 , , 则菱形的面积为 . 16. 如图,把长方形纸片OABC放入平面直角坐标系中,使OA , OC分别落在x轴、y轴上,连接AC , 将纸片OABC沿AC折叠,使点B落在点D位置,AD与y轴交于点E , 若 , 则OE长为 .
16. 如图,把长方形纸片OABC放入平面直角坐标系中,使OA , OC分别落在x轴、y轴上,连接AC , 将纸片OABC沿AC折叠,使点B落在点D位置,AD与y轴交于点E , 若 , 则OE长为 . 17. 如图,OP=1,过P作且 , 由勾股定理得 , 再过作且 . 得 . 又过作且 , 得;…依此类推,得 .
17. 如图,OP=1,过P作且 , 由勾股定理得 , 再过作且 . 得 . 又过作且 , 得;…依此类推,得 . 18. 如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是 .
18. 如图,已知平行四边形ABCD中,AB=BC,BC=10,∠BCD=60°,两顶点B、D分别在平面直角坐标系的y轴、x轴的正半轴上滑动,连接OA,则OA的长的最小值是 .
三、解答题(本大题9小题,共66分)
-
19. 计算:20. 正方形的边长为a cm,它的面积与长为10cm,宽为8cm的长方形的面积相等,求a的值.21. 如图,在笔直的铁路上A、B两点相距7km,C , D为两村庄,DA=3km.CB=4km,DA⊥AB于A , CB⊥AB于B . 现要在AB上建一个中转站E , 使得C , D两村到E站的距离相等,求AE的长.
 22. 如图.在Rt△ABC中,∠ACB=90°,CD⊥AB于D , 2∠ACD=∠BCD , E是斜边AB的中点,∠ECD是多少度?为什么?
22. 如图.在Rt△ABC中,∠ACB=90°,CD⊥AB于D , 2∠ACD=∠BCD , E是斜边AB的中点,∠ECD是多少度?为什么? 23. 如图,在四边形ABCD中,∠BAC=∠ACD=90°, , 点E是CD的中点.
23. 如图,在四边形ABCD中,∠BAC=∠ACD=90°, , 点E是CD的中点. (1)、求证:四边形ABCE是平行四边形;(2)、若AC=4, . 求四边形ABCE的面积.24.
(1)、求证:四边形ABCE是平行四边形;(2)、若AC=4, . 求四边形ABCE的面积.24. (1)、如图1,在4×4的网格中,每小格的边长为1,请你画出一条长为的线段MN;(2)、如图2,在平面直角坐标系中有A(2,4),B(5,3).以A、B、C为顶点的三角形是等腰直角三角形时,直接写出所有满足条件的C点坐标.25. 如图,已知边长为3的正方形ABCD , E为CD边上一点,DE=1,将△ADE沿AE翻折得到△AFE , 延长CB至点G , 使BG=DE , 连接AG , FG .
(1)、如图1,在4×4的网格中,每小格的边长为1,请你画出一条长为的线段MN;(2)、如图2,在平面直角坐标系中有A(2,4),B(5,3).以A、B、C为顶点的三角形是等腰直角三角形时,直接写出所有满足条件的C点坐标.25. 如图,已知边长为3的正方形ABCD , E为CD边上一点,DE=1,将△ADE沿AE翻折得到△AFE , 延长CB至点G , 使BG=DE , 连接AG , FG . (1)、求证:AE=AG;(2)、求FG的长.26. 如图,已知矩形ABCD , AD=4,CD=10,P是AB上一动点,M , N , E分别是PD , PC , CD的中点.
(1)、求证:AE=AG;(2)、求FG的长.26. 如图,已知矩形ABCD , AD=4,CD=10,P是AB上一动点,M , N , E分别是PD , PC , CD的中点. (1)、求证:四边形PMEN是平行四边形;(2)、当AP=2时,判断四边形PMEN是什么图形,并证明你的结论;(3)、当四边形PMEN为菱形时,求AP的值.27. 在矩形ABCD中,CD=3,连接BD , 且∠CBD=30°,将三角形BDC沿BD翻折得 , 交AD于G , 连接 .
(1)、求证:四边形PMEN是平行四边形;(2)、当AP=2时,判断四边形PMEN是什么图形,并证明你的结论;(3)、当四边形PMEN为菱形时,求AP的值.27. 在矩形ABCD中,CD=3,连接BD , 且∠CBD=30°,将三角形BDC沿BD翻折得 , 交AD于G , 连接 . (1)、如图(1)判断与BD的位置关系和数量关系,并证明;(2)、如图若沿线段BD由B向D运动,速度每秒1个单位,连接 .
(1)、如图(1)判断与BD的位置关系和数量关系,并证明;(2)、如图若沿线段BD由B向D运动,速度每秒1个单位,连接 .①如图(2)当t=1.5时,判断四边形的形状,并证明;
②如图(3)在运动过程中,四边形的面积是否发生变化?若不变,求出面积,若变化,说明理由.