四川省绵阳市2024年中考数学模拟试题（五）

试卷更新日期：2024-05-28 类型：中考模拟

进入出卷网下载

一、选择题：本大题共12个小题，每小题3分，共36分．每个小题只有一个选项符合题要求．

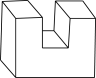
1. 在0， $\sqrt{3}$ ，-3，2这四个数中，最大的数是（）

A、0 B、 $\sqrt{3}$ C、-3 D、2

查看试题解析
2. 2020年，新冠肺炎在全球肆虐，截止9月下旬，全球已经约有38703120人确诊，将38703120用科学记数法表示为（）

A、38.70312×10⁶ B、3.870312×10⁷ C、3.870312×10⁶ D、3.870312×10⁸

查看试题解析
3. 某几何体如图所示，该几何体的左视图是（）

A、 B、 C、 D、

查看试题解析
4. 如图，∠ACD是△ABC的外角，CE∥AB，若∠ACB=75°，∠ECD=50°，则∠A的度数为（）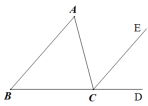

A、50° B、55° C、70° D、75°

查看试题解析
5. 明代程大位有一首类似二元一次方程组的饮酒数学诗，现进行了变式，大意是：好酒二瓶，可以醉倒5位客人；薄酒三瓶，可以醉倒二位客人，如果29位客人醉倒了，他们总共饮下16瓶酒．试问：其中好酒、薄酒分别是多少瓶?设有好酒 $x$ 瓶，薄酒 $y$ 瓶。依题意，可列方程组为（）

A、 ${\begin{array}{l} x + y = 16 \\ \frac{2}{5} x + \frac{2}{3} y = 29 \end{array}$ B、 ${\begin{array}{l} x + y = 16 \\ 2.5 x + \frac{2}{3} y = 29 \end{array}$ C、 ${\begin{array}{l} x + y = 16 \\ 5 x + 3 y = 29 \end{array}$ D、 ${\begin{array}{l} x + y = 16 \\ 2.5 x + \frac{3}{2} y = 29 \end{array}$

查看试题解析
6. 下列汉字中，是轴对称图形的是（）

A、喜 B、迎 C、冬 D、奥

查看试题解析
7. 一组数据 $x_{1} ， x_{2} ， x_{3} ， \dots \dots ， x_{n}$ 的极差是3，则另一组数据 $x_{1} + 1 ， x_{2} + 1 ， x_{3} + 1 ， \dots \dots ， x_{n} + 1$ 的极差是（）

A、3　　　 B、4　　　 C、6　　　 D、9

查看试题解析
8. 如图，等边△ABC的周长为6π，半径是1的⊙O从与AB相切于点D的位置出发，在△ABC外部按顺时针方向沿三角形滚动，又回到与AB相切于点D的位置，则⊙O自转了（）

A、2周 B、3周 C、4周 D、5周

查看试题解析
9. 如果不等式组 $\{\begin{matrix} x < 8 \\ x > m \end{matrix}$ 无解，那么m的取值范围是（　　）

A、m＞8 B、m≥8 C、m＜8 D、m≤8

查看试题解析
10.
如图，已知在正方形ABCD中，点E、F分别在BC、CD上，△AEF是等边三角形，连接AC交EF于G，给出下列结论：
①BE=DF；②∠DAF=15°；③AC垂直平分EF；④BE+DF=EF．
其中结论正确的共有（　　）

A、1个 B、2个 C、3个 D、4个

查看试题解析
11. 无理数2 $\sqrt{11}$ ﹣3在（）

A、2和3之间 B、3和4之间 C、4和5之间 D、5和6之间

查看试题解析
12. 如图所示，在Rt $△ A B C$ 中， $∠ C = 90 °$ ， $A C = 8$ ， $A B = 10$ ，点 $O$ 为 $B C$ 上的点， $⊙ O$ 的半径 $O C = 1$ ，点 $D$ 是 $A B$ 边上的动点，过点 $D$ 作⊙ $O$ 的一条切线 $D E$ （点 $E$ 为切点），则线段 $D E$ 的最小值为（　　）

A、 $3 \sqrt{2} - 1$ B、 $\sqrt{15}$ C、 $\sqrt{15} - 1$ D、4

查看试题解析

二、填空题：本大题共6个小题，每小题4分，共24分．将答案填写在答题卡相应的横线上．

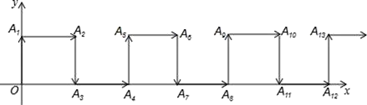
13. 分解因式：x²y+2xy²+y³ ．

查看试题解析
14. 如图，在平面直角坐标系中，一动点从原点O出发，按向上、向右、向下、向右的方向依次平移，每次移动一个单位，得到点A₁(0，1)，A₂(1，1)，A₃(1，0)，A₄(2，0)，…那么点A₂₀₂₂的坐标为.

查看试题解析
15. 使二次根式 $\sqrt{1 - \frac{1}{2} x}$ 有意义的x的取值范围是．

查看试题解析
16. 如图OC是⊙O的半径，弦AB⊥OC于点D，点E在⊙O上，EB恰好经过圆心O．连接EC．若∠B＝∠E，OD＝ $\frac{3}{2}$ ，则劣弧AB的长为．

查看试题解析
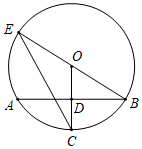17. $A ， B$ 两市相距150千米，甲车从 $A$ 市到 $B$ 市，乙车从 $B$ 市到 $A$ 市，两车同时出发，已知甲车速度比乙车快20千米/小时，甲车比乙车早半小时到达目的地．若设乙车的速度是 $x$ 千米/小时，则根据题意，可列方程．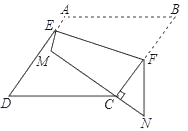

查看试题解析
18. 如图，在菱形 $A B C D$ 中， $\sin B = \frac{4}{5}$ ，点 $E ， F$ 分别在边 $A D ， B C$ 上，将四边形 $A E F B$ 沿 $E F$ 翻折，使 $A B$ 的对应线段 $M N$ 经过顶点 $C$ ，当 $M N ⊥ B C$ 时， $\frac{A E}{A D}$ 的值是．

查看试题解析

三、解答题：本大题共7个小题，共90分．解答应写出文字说明、证明过程或演算步骤．

19. 计算：3tan30°＋cos²45°－2sin60°．

查看试题解析
20. 一个不透明的布袋中装有4个只有颜色不同的球，其中有1个黄球、1个白球、2个红球．

(1)、任意摸出1个球，记下颜色后不放回，再任意摸出1个球．求两次摸出的球恰好都是红球的概率（要求画树状图或列表）；

(2)、现再将n个黄球放入布袋，搅匀后，使任意摸出1个球是黄球的概率为 $\frac{1}{2}$ ，求n的值．

查看试题解析
21. 甲、乙两车从A城出发匀速行驶至B城．在整个行驶过程中，甲、乙两车离开A城的距离y（km）与甲车行驶的时间t（h）之间的函数关系如图所示．

(1)、A，B两城相距千米；

(2)、当1≤t≤4时，求乙车离开A城的距离y（km）与甲车行驶的时间t（h）之间的函数关系式；

(3)、乙车出发后小时追上甲车．

查看试题解析
22. 已知：如图，在△BAC中，AB=AC，D，E分别为AB，AC边上的点，且DE∥BC，求证：△DAE是等腰三角形．

查看试题解析
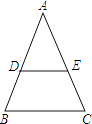23. 在平面直角坐标系中，O为原点，直线l：x=1，点A（2，0），点E，点F，点M都在直线l上，且点E和点F关于点M对称，直线EA与直线OF交于点P．

(1)、若点M的坐标为（1，﹣1），
①当点F的坐标为（1，1）时，如图，求点P的坐标；
②当点F为直线l上的动点时，记点P（x，y），求y关于x的函数解析式．

(2)、若点M（1，m），点F（1，t），其中t≠0，过点P作PQ⊥l于点Q，当OQ=PQ时，试用含t的式子表示m．

查看试题解析
24. 如图，已知：在△ABC中， $∠ C = 9 0^{∘}$ ，点P是BC边上的动点. $P D ⊥ B C$ 交AB于D.以PD为直径的⊙O分别交AB，AP于点E，F.

(1)、求证： $∠ E F P = ∠ E P B$ .

(2)、若 $A B = 20$ ， $s i n B = \frac{3}{5}$ .
①当 $∠ A P B = 4 ∠ A P D$ ，求PC的长.

②当△PEF为等腰三角形时，请求出所有满足条件的△PEF的腰长.

(3)、若 $s i n B = \frac{\sqrt{2}}{2}$ ，且D，F，C在一条直线上，则DP与AC的比值为.

查看试题解析
25. 如图，抛物线y＝ $\frac{8}{15}$ x²+bx+c过点A（2，0）和B（3，3）.

(1)、求抛物线的表达式；

(2)、点M在第二象限的抛物线上，且∠MBO＝∠ABO.
①直线BM交x轴于点N，求线段ON的长；
②延长BO交抛物线于点C，点P是平面内一点，连接PC、OP，当△POC∽△MOB时，请直接写出点P的坐标.

查看试题解析