2024年广东省深圳市中考数学全真模拟试卷(八)

试卷更新日期：2024-05-28 类型：中考模拟

进入出卷网下载

一、选择题(本题共10小题，共30分，每小题有4个选项，只有一个正确选项)

1. 华为Mate60Pro手机是全球首款支持卫星通话的智能手机．预计至2024年底，这款手机的出货量将达到70000000台．将70000000用科学记数法表示应为（）

A、 $7 \times 10^{8}$ B、 $70 \times 10^{6}$ C、 $7 \times 10^{7}$ D、 $0.7 \times 10^{8}$

查看试题解析
2. 我国杨秉烈先生在上世纪八十年代发明了繁花曲线规画图工具，利用该工具可以画出许多漂亮的繁花曲线，繁花曲线的图案在服装、餐具等领域都有广泛运用．下面四种繁花曲线中，是轴对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
3. 下列运算正确的是（）

A、m²+2m＝3m³ B、（2m²）³＝6m⁶ C、m²•m³＝m⁶ D、m⁴÷m²＝m²

查看试题解析
4. 若关于 $x$ ， $y$ 的二元一次方程组 ${\begin{array}{l} x - 3 y = 4 m - 13 \\ x + 5 y = 5 \end{array}$ 的解满足 $x + y \leq 0$ ，则 $m$ 的取值范围是（）

A、 $m \leq 2$ B、 $m < 2$ C、 $m > 2$ D、 $m \geq 2$

查看试题解析
5. 已知关于x的一元二次方程 $k x^{2} - (4 k - 1) x + 4 k - 3 = 0$ 有两个不相等的实数根，则实数k的取值范围是（）

A、 $k < \frac{1}{4}$ B、 $k < \frac{1}{4}$ 且 $k \neq 0$ C、 $k > - \frac{1}{4}$ D、 $k > - \frac{1}{4}$ 且 $k \neq 0$

查看试题解析
6. 如图， $△ A B C$ 的顶点都是正方形网格中的格点，则 $c o s ∠ A B C$ 等于（）

A、 $\sqrt{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{2}{3}$

查看试题解析
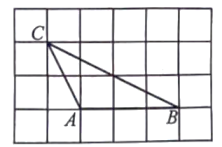7. 如图，在平面直角坐标系中，菱形ABCD的顶点A在y轴的正半轴上，顶点B ， C在x轴的正半轴上， $D (2 ， \sqrt{3})$ ， $P (- 1 ， - 1)$ ，点M在菱形的边AD和DC上运动 $($ 不与点A ， C重合 $)$ ，过点M作 $M N / / y$ 轴，与菱形的另一边交于点N ，连接PM ， PN ，设点M的横坐标为x ， $△ P M N$ 的面积为y ，则下列图象能正确反映y与x之间函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题(本题5小题，每题3分，共15分)

8. 因式分解： $3 {ax}^{2} - 12 {ay}^{2} =$ ．

查看试题解析
9. 若关于x的一元一次不等式组 $\{\begin{matrix} \frac{x + 3}{2} \leq 4 ， \\ 2 x - a \geq 2 \end{matrix}$ 至少有2个整数解，且关于y的分式方程 $\frac{a - 1}{y - 2} + \frac{4}{2 - y} = 2$ 有自然数解，则所有满足条件的整数a的值之和是.

查看试题解析
10. 一个仅装有球的不透明布袋里只有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为 $\frac{2}{3}$ ，则n=.

查看试题解析
11. 如图，已知直线 $y = - \frac{2}{3} x + 2$ 与坐标轴交于 $A$ ， $B$ 两点，矩形 $A B C D$ 的对称中心为 $M$ ，双曲线 $y = \frac{k}{x} (x > 0)$ 正好经过 $C$ ， $M$ 两点，则直线 $A C$ 的解析式为．

查看试题解析
12. 如图，在矩形ABCD中，AB=3，BC=4.点E在边AD上，且ED=3，M，N分别是边AB，BC上的动点，且 BM=BN，P是线段CE 上的动点，连结PM，PN.若PM+PN=4，则线段PC的长为.

查看试题解析

三、解答题(本题共7小题，其中第16题6分，第17题7分，第18题8分，第19题7分，第20题9分，第21题9分，第22题10分)

13. 计算： $(π - 4)^{0} + | - \sqrt{2} | - 2 c o s 60 ° - \sqrt{18}$ ．

查看试题解析
14. 先化简，再求值： $(\frac{3}{a - 1} + \frac{a - 3}{a^{2} - 1}) \div \frac{a}{a + 1}$ ，其中a= $\sqrt{2}$ +1．

查看试题解析
15. 在10×6的网格中建立如图的平面直角坐标系，△ABC的顶点坐标分别为A（0，3），B（6，3），C（4，6）仅用无刻度的直尺在给定网格中按要求完成画图.

(1)、在CB上找点D，使AD平分∠BAC；

(2)、在AB上找点F，使∠CFA＝∠DFB；

(3)、在BC上找点M、N，使BM＝MN＝NC.[（1）（2）画在图1中，（3）画在图2中].

查看试题解析
16. 已知 $A$ ， $B$ ， $C$ ， $D$ ， $E$ 五个红色研学基地，某地为了解中学生的意愿，随机抽取部分学生进行调查，并将统计数据整理后，绘制了不完整的条形统计图和扇形统计图．

(1)、请将条形统计图补充完整；

(2)、在扇形统计图中， $D$ 所在的扇形的圆心角的度数为；若该地区有1000名中学生参加研学活动，则愿意去 $A$ 基地的大约有人；

(3)、甲、乙两所学校计划从 $A$ ， $B$ ， $C$ 三个基地中任选一个基地开展研学活动，请利用树状图或表格求两校恰好选取同一个基地的概率．

查看试题解析
17. 2022年3月25日，教育部印发《义务教育课程方案》和《课程标准（2022年版）》，优化了课程设置，将劳动从综合与实践课程中独立出来．为了体验劳动的快乐，亲历劳动的过程，某班组织学生到菜园进行了蔬菜采摘活动．班主任将该班学生分成甲、乙两组，在相同的采摘时间内，甲组采摘了270千克，乙组采摘了225千克，平均每小时甲组比乙组多采摘30千克，请用列方程的方法求平均每小时甲、乙两个小组各采摘多少千克．

查看试题解析
18.
如图，在平面直角坐标系中，直线 $y = a x + 1$ 与y轴交于点A ，与双曲线 $y = \frac{k}{x} (x > 0)$ 的交点为 $B (p, 3)$ ，且 $△ A O B$ 的面积为 $\frac{4}{3}$ ．

(1)、求a ， k的值；

(2)、直线 $y = m x - 8 m + 1$ 与双曲线 $y = \frac{k}{x} (x > 0)$ 的交点为C ， D（C在D的左边）．
①连接AC ， AD ，若 $△ A C D$ 的面积为24，求点C的坐标；
②直线 $y = 7$ 与直线 $y = m x - 8 m + 1$ 交于点E ，过点D作 $D F ⊥ D E$ ，交直线 $y = 7$ 于点F ， G为线段DF上一点，且 $D G = \frac{3}{4} D E$ ，连接AG ，求 $\frac{4}{3} A G + A E$ 的最小值．

查看试题解析
19. 【推理】
如图1，在正方形 $A B C D$ 中，点 $E$ 是 $C D$ 上一动点，将正方形沿着 $B E$ 折叠，点 $C$ 落在点 $F$ 处，连结 $B E$ ， $C F$ ，延长 $C F$ 交 $A D$ 于点 $G$ ．

(1)、求证： $△ B C E$ ≌ $△ C D G$ ．

(2)、如图2，在【推理】条件下，延长 $B F$ 交 $A D$ 于点 $H .$ 若 $\frac{H D}{H F} = \frac{4}{5}$ ， $C E = 9$ ，求线段 $D E$ 的长．

(3)、将正方形改成矩形，同样沿着 $B E$ 折叠，连结 $C F$ ，延长 $C F$ ， $B F$ 交直线 $A D$ 于 $G$ ， $H$ 两点，若 $\frac{A B}{B C} = k$ ， $\frac{H D}{H F} = \frac{4}{5}$ ，求 $\frac{D E}{E C}$ 的值 $($ 用含 $k$ 的代数式表示 $)$ ．

查看试题解析