湖南省常德市澧县2024年中考数学最后一模试卷

试卷更新日期：2024-05-28 类型：中考模拟

进入出卷网下载

一、选择题（共10小题，每小题3分，共30分）

1.
如图，菱形中，对角线AC、BD交于点O ， E为AD边中点，菱形ABCD的周长为28，则OE的长等于（　　）

A、3.5 B、4 C、7 D、14

查看试题解析
2. 从①②③④中选择一块拼图板可与左边图形拼成一个正方形，正确的选择为（　　）

A、① B、② C、③ D、④

查看试题解析
3. 如图，在正方形ABCD中，G为CD边中点，连接AG并延长，分别交对角线BD于点F，交BC边延长线于点E.若FG＝2，则AE的长度为（）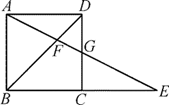

A、6 B、8 C、10 D、12

查看试题解析
4. 如图， $Δ A B C$ 为等边三角形，要在 $Δ A B C$ 外部取一点 $D$ ，使得 $Δ A B C$ 和 $Δ D B C$ 全等，下面是两名同学做法：（）
甲：①作 $∠ A$ 的角平分线 $l$ ；②以 $B$ 为圆心， $B C$ 长为半径画弧，交 $l$ 于点 $D$ ，点 $D$ 即为所求；
乙：①过点 $B$ 作平行于 $A C$ 的直线 $l$ ；②过点 $C$ 作平行于 $A B$ 的直线 $m$ ，交 $l$ 于点 $D$ ，点 $D$ 即为所求．

A、两人都正确 B、两人都错误 C、甲正确，乙错误 D、甲错误，乙正确

查看试题解析
5. 点A(－1，y₁)，B(－2，y₂)在反比例函数y＝ $\frac{2}{x}$ 的图象上，则y₁ ， y₂的大小关系是（）

A、y₁＞y₂ B、y₁＝y₂ C、y₁＜y₂ D、不能确定

查看试题解析
6. 某药品经过两次降价，每瓶零售价由168元降为108元，已知两次降价的百分率相同，设每次降价的百分率为x ，根据题意列方程得（）

A、168（1﹣x）²＝108 B、168（1﹣x²）＝108 C、168（1﹣2x）＝108 D、168（1+x）²＝108

查看试题解析
7. 已知⊙O的半径为5，弦AB=6，P是AB上任意一点，点C是劣弧 $\overset{⌢}{A B}$ 的中点，若△POC为直角三角形，则PB的长度（　　）

A、1 B、5 C、1或5 D、2或4

查看试题解析
8. 如图，在菱形ABCD中，∠A=60°，E是AB边上一动点（不与A、B重合），且∠EDF=∠A，则下列结论错误的是（　　）

A、AE=BF B、∠ADE=∠BEF C、△DEF是等边三角形 D、△BEF是等腰三角形

查看试题解析
9. 九年级学生去距学校10 km的博物馆参观，一部分学生骑自行车先走，过了20 min后，其余学生乘汽车出发，结果他们同时到达.已知汽车的速度是骑车学生速度的2倍，求骑车学生的速度.设骑车学生的速度为x km/h，则所列方程正确的是（）

A、 $\frac{10}{x} = \frac{10}{2 x} - \frac{1}{3}$ B、 $\frac{10}{x} = \frac{10}{2 x} - 20$ C、 $\frac{10}{x} = \frac{10}{2 x} + \frac{1}{3}$ D、 $\frac{10}{x} = \frac{10}{2 x} + 20$

查看试题解析
10. 若代数式 $\frac{1}{x - 1}$ + $\sqrt{x}$ 有意义，则实数x的取值范围是（）

A、x≠1 B、x≥0 C、x≠0 D、x≥0且x≠1

查看试题解析

二、填空题（本大题共6个小题，每小题3分，共18分）

11. 一元二次方程x﹣1＝x²﹣1的根是．

查看试题解析
12. 有一枚质地均匀的骰子，六个面分别表有1到6的点数，任意将它抛掷两次，并将两次朝上面的点数相加，则其和小于6的概率是．

查看试题解析
13. 已知关于x，y的二元一次方程组 ${\begin{matrix} 2 x + 3 y = k \\ x + 2 y = - 1 \end{matrix}$ 的解互为相反数，则k的值是．

查看试题解析
14. 已知x+ $\frac{1}{x}$ =6，则x²+ $\frac{1}{x^{2}}$ =.

查看试题解析
15. π﹣3的绝对值是．

查看试题解析
16. 因式分解：9x﹣x²= ．

查看试题解析

三、解答题（共8题，共72分）

17. 先化简，再求值： $(x - 1) \div (\frac{2}{x + 1} - 1)$ ，其中x为方程 $x^{2} + 3 x + 2 = 0$ 的根.

查看试题解析
18. 如图（1），AB=CD，AD=BC，O为AC中点，过O点的直线分别与AD、BC相交于点M、N，那么∠1与∠2有什么关系？请说明理由；
若过O点的直线旋转至图（2）、（3）的情况，其余条件不变，那么图（1）中的∠1与∠2的关系成立吗？请说明理由．

查看试题解析
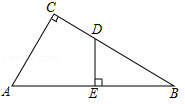
19. 在“弘扬传统文化，打造书香校园”活动中，学校计划开展四项活动：“A-国学诵读”、“B-演讲”、“C-课本剧”、“D-书法”，要求每位同学必须且只能参加其中一项活动，学校为了了解学生的意思，随机调查了部分学生，结果统计如下：

(1)、根据题中信息补全条形统计图．

(2)、所抽取的学生参加其中一项活动的众数是．

(3)、学校现有800名学生，请根据图中信息，估算全校学生希望参加活动A有多少人？

查看试题解析
20. 如图，已知 $△ A B C$ ，请用尺规过点 $C$ 作一条直线，使其将 $△ A B C$ 分成面积比为 $1 : 3$ 两部分．（保留作图痕迹，不写作法）

查看试题解析
21. 如图，已知一次函数 $y = k x + b$ 的图象与反比例函数 $y = \frac{8}{x}$ 的图象交于A，B两点，点A的横坐标是2，点B的纵坐标是-2。

(1)、求一次函数的解析式；

(2)、求 $Δ A O B$ 的面积。

查看试题解析
22. 现种植A、B、C三种树苗一共480棵，安排80名工人一天正好完成，已知每名工人只植一种树苗，且每名工人每天可植A种树苗8棵；或植B种树苗6棵，或植C种树苗5棵．经过统计，在整个过程中，每棵树苗的种植成本如图所示．设种植A种树苗的工人为x名，种植B种树苗的工人为y名．求y与x之间的函数关系式；设种植的总成本为w元，

(1)、求w与x之间的函数关系式；

(2)、若种植的总成本为5600元，从植树工人中随机采访一名工人，求采访到种植C种树苗工人的概率．

查看试题解析
23. 如图，Rt△ABC中，∠C=90°，AB=14，AC=7，D是BC上一点，BD=8，DE⊥AB，垂足为E，求线段DE的长．

查看试题解析
24. 如图，在△OAB中，OA=OB，C为AB中点，以O为圆心，OC长为半径作圆，AO与⊙O交于点E，OB与⊙O交于点F和D，连接EF，CF，CF与OA交于点G

(1)、求证：直线AB是⊙O的切线；

(2)、求证：△GOC∽△GEF；

(3)、若AB=4BD，求sinA的值.

查看试题解析