湖南省邵阳市邵东县2024年中考数学三轮冲刺卷综合练习试题

试卷更新日期：2024-05-28 类型：中考模拟

进入出卷网下载

一、选择题（本大题共12个小题，每小题4分，共48分．在每小题给出的四个选项中，只有一项是符合题目要求的．）

1. 已知二次函数 $y = a x^{2} + b x + c$ 图象上部分点的坐标对应值列表如下：
x
…
-3
-2
-1
0
1
2
…
y
…
2
-1
-2
-1
2
7
…
则该函数图象的对称轴是（）

A、x=-3 B、x=-2 C、x=-1 D、x=0

查看试题解析
2.
如图，直线AB∥CD，∠C=44°，∠E为直角，则∠1等于（　　）

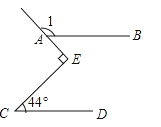A、132° B、134° C、136° D、138°

查看试题解析
3. 用加减法解方程组 ${\begin{array}{l} 4 x + 3 y = 7 ① \\ 6 x - 5 y = - 1 ② \end{array}$ 时，若要求消去 $y$ ，则应（）

A、 $① \times 3 + ② \times 2$ B、 $① \times 3 - ② \times 2$ C、 $① \times 5 + ② \times 3$ D、 $① \times 5 - ② \times 3$

查看试题解析
4. 如图，在 $R t Δ A B C$ 中， $∠ A C B = 90 °$ ， $t a n ∠ C A B = \frac{\sqrt{3}}{3}$ ， $A B = 3$ ，点 $D$ 在以斜边 $A B$ 为直径的半圆上，点 $M$ 是 $C D$ 的三等分点，当点 $D$ 沿着半圆，从点 $A$ 运动到点 $B$ 时，点 $M$ 运动的路径长为（）

A、 $π$ 或 $\frac{π}{2}$ B、 $\frac{π}{2}$ 或 $\frac{π}{3}$ C、 $\frac{π}{3}$ 或 $π$ D、 $\frac{π}{4}$ 或 $\frac{π}{3}$

查看试题解析
5. 对于数据：6，3，4，7，6，0，9．下列判断中正确的是（）

A、这组数据的平均数是6，中位数是6 B、这组数据的平均数是6，中位数是7 C、这组数据的平均数是5，中位数是6 D、这组数据的平均数是5，中位数是7

查看试题解析
6. 如图，在半径为5的⊙O中，弦AB=6，点C是优弧 $\overset{⌢}{A B}$ 上一点（不与A，B重合），则cosC的值为（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
7. 如图，四边形ABCD中，AC⊥BC，AD∥BC，BC=3，AC=4，AD=6．M是BD的中点，则CM的长为（　　）

A、 $\frac{3}{2}$ B、2 C、 $\frac{5}{2}$ D、3

查看试题解析
8. 如图，在矩形ABCD中，AB=2，BC=3．若点E是边CD的中点，连接AE，过点B作BF⊥AE交AE于点F，则BF的长为（　　）

A、 $\frac{3 \sqrt{10}}{2}$ B、 $\frac{3 \sqrt{10}}{5}$ C、 $\frac{\sqrt{10}}{5}$ D、 $\frac{3 \sqrt{5}}{5}$

查看试题解析
9. 如图，将△ABC绕点B顺时针旋转60°得△DBE，点C的对应点E恰好落在AB的延长线上，连接AD，下列结论不一定正确的是（　　）

A、AD∥BC B、∠DAC=∠E C、BC⊥DE D、AD+BC=AE

查看试题解析
10. 方程 $\frac{x - 2}{x - 3} = \frac{x}{x + 1}$ 的解为（　　）

A、x=﹣1 B、x=1 C、x=2 D、x=3

查看试题解析
11. 实数a ， b ， c在数轴上对应点的位置大致如图所示，O为原点，则下列关系式正确的是(　　)

A、a﹣c＜b﹣c B、|a﹣b|＝a﹣b C、ac＞bc D、﹣b＜﹣c

查看试题解析
12. 数轴上分别有A、B、C三个点，对应的实数分别为a、b、c且满足，|a|＞|c|，b•c＜0，则原点的位置（　　）

A、点A的左侧 B、点A点B之间 C、点B点C之间 D、点C的右侧

查看试题解析

二、填空题：（本大题共6个小题，每小题4分，共24分．）

13. 若关于x的方程 $2 x^{2} + x - a = 0$ 有两个不相等的实数根，则实数a的取值范围是。

查看试题解析
14. 意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，请根据这组数的规律写出第10个数是．

查看试题解析
15.
如图，在Rt△ABC中，∠A=90°，AB=AC，BC=20，DE是△ABC的中位线，点M是边BC上一点，BM=3，点N是线段MC上的一个动点，连接DN，ME，DN与ME相交于点O．若△OMN是直角三角形，则DO的长是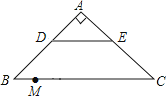

查看试题解析
16. 对于一元二次方程 $x^{2} - 5 x + 2 = 0$ ，根的判别式 $b^{2} - 4 a c$ 中的 $b$ 表示的数是．

查看试题解析
17. 因式分解： $x^{3} y^{2} - x^{3} =$ ．

查看试题解析
18. 如图，在矩形ABCD中，过点A的圆O交边AB于点E，交边AD于点F，已知AD=5，AE=2，AF=4．如果以点D为圆心，r为半径的圆D与圆O有两个公共点，那么r的取值范围是．

查看试题解析

三、解答题：（本大题共9个小题，共78分，解答应写出文字说明、证明过程或演算步骤．

19. 关于x的一元二次方程x²﹣（2m﹣3）x+m²+1=1．

(1)、若m是方程的一个实数根，求m的值；

(2)、若m为负数，判断方程根的情况．

查看试题解析
20. 如图，已知A（﹣4， $\frac{1}{2}$ ），B（﹣1，m）是一次函数y＝kx+b与反比例函数y $= \frac{n}{x}$ 图象的两个交点，AC⊥x轴于点C ， BD⊥y轴于点D ．

(1)、求m的值及一次函数解析式；

(2)、P是线段AB上的一点，连接PC、PD ，若△PCA和△PDB面积相等，求点P坐标．

查看试题解析
21. 化简求值： $\frac{x - 1}{x^{2} + 2 x + 1} \div (1 - \frac{2}{x + 1})$ ，其中x是不等式组 ${\begin{array}{l} 2 x - 7 < 3 (x - 1) ① \\ \frac{4}{3} x + 3 \leq 1 - \frac{2}{3} x ② \end{array}$ 的整数解．

查看试题解析
22. 如图，△DEF是由△ABC通过一次旋转得到的，请用直尺和圆规画出旋转中心．

查看试题解析
23. 如图，四边形ABCD，AD∥BC，DC⊥BC于C点，AE⊥BD于E，且DB＝DA.求证：AE＝CD.

查看试题解析
24. 在 $△ A B C$ 中， $∠ A B C = 9 0^{∘}$ ， BD为AC边上的中线，过点C作 $C E ⊥ B D$ 于点E，过点A作BD的平行线，交CE的延长线于点F，在AF的延长线上截取 $F G = B D$ ，连接BG，DF．

(1)、求证： $B D = D F$ ；

(2)、求证：四边形BDFG为菱形；

(3)、若 $A G = 5$ ， $C F = \sqrt{7}$ ，求四边形BDFG的周长．

查看试题解析
25.

(1)、计算：|﹣2|﹣（π﹣2015）⁰+（ $\frac{1}{2}$ ）^﹣2﹣2sin60°+ $\sqrt{12}$ ；

(2)、先化简，再求值： $\frac{a^{2} - 1}{a^{2} - a}$ ÷（2+ $\frac{a^{2} + 1}{a}$ ），其中a= $\sqrt{2}$ ．

查看试题解析
26. 某工厂准备用图甲所示的A型正方形板材和B型长方形板材，制作成图乙所示的竖式和横式两种无盖箱子．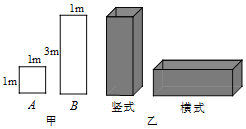

(1)、若该工厂准备用不超过10000元的资金去购买A，B两种型号板材，并全部制作竖式箱子，已知A型板材每张30元，B型板材每张90元，求最多可以制作竖式箱子多少只？

(2)、若该工厂仓库里现有A型板材65张、B型板材110张，用这批板材制作两种类型的箱子，问制作竖式和横式两种箱子各多少只，恰好将库存的板材用完？

(3)、若该工厂新购得65张规格为 $3 \times 3 m$ 的C型正方形板材，将其全部切割成A型或B型板材 $($ 不计损耗 $)$ ，用切割成的板材制作两种类型的箱子，要求竖式箱子不少于20只，且材料恰好用完，则能制作两种箱子共只 $.$

查看试题解析
27. 如图，AB为 $⊙ O$ 的直径，直线 $B M ⊥ A B$ 于点B.点C在 $⊙ O$ 上，分别连接 $B C$ ， $A C$ ，且 $A C$ 的延长线交 $B M$ 于点D. $C F$ 为 $⊙ O$ 的切线交 $B M$ 于点F.

(1)、求证： $C F = D F$ ；

(2)、连接 $O F$ . 若 $A B = 10$ ， $B C = 6$ ，求线段 $O F$ 的长.

查看试题解析

x	…	-3	-2	-1	0	1	2	…
y	…	2	-1	-2	-1	2	7	…