2024年广东省深圳市中考数学全真模拟试卷(六)
试卷更新日期:2024-05-28 类型:中考模拟
一、选择题(本题共10小题,每小题3分,共30分,每题有4个选项同,只有一个正确)
-
1. 在实数 , , , , , 9中,无理数有( )A、1个 B、2个 C、3个 D、4个2. “春江潮水连海平,海上明月共潮生”,水是诗人钟爱的意象,经测算,一个水分子的直径约为 , 数据用科学记数法表示为( )A、 B、 C、 D、3. 下列所示的图案分别是奔驰、雪铁龙、大众、三菱汽车的车标,其中可以看作由“基本图案”经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 4. 如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形是三角板),其依据是( )
4. 如图,过直线外一点画已知直线的平行线的方法叫“推平行线”法(图中三角形是三角板),其依据是( ) A、同旁内角互补,两直线平行 B、两直线平行,同旁内角互补 C、同位角相等,两直线平行 D、两直线平行,同位角相等5. 下列判断不正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 在《代数学》中记载了求方程x2+8x=33正数解的几何方法:如图1,先构造一个面积为x2的正方形,再以正方形的边为一边向外构造四个面积为2x的矩形,得到大正方形的面积为33+16=49,则该方程的正数解为7﹣4=3.小明尝试用此方法解关于x的方程x2+10x+c=0时,构造出如图2所示正方形.已知图2中阴影部分的面积和为39,则该方程的正数解为( )
A、同旁内角互补,两直线平行 B、两直线平行,同旁内角互补 C、同位角相等,两直线平行 D、两直线平行,同位角相等5. 下列判断不正确的是( )A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则6. 在《代数学》中记载了求方程x2+8x=33正数解的几何方法:如图1,先构造一个面积为x2的正方形,再以正方形的边为一边向外构造四个面积为2x的矩形,得到大正方形的面积为33+16=49,则该方程的正数解为7﹣4=3.小明尝试用此方法解关于x的方程x2+10x+c=0时,构造出如图2所示正方形.已知图2中阴影部分的面积和为39,则该方程的正数解为( )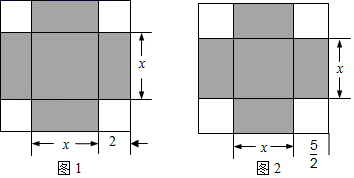 A、2 B、2 C、3 D、47. 如图是一盏可调节台灯及其示意图.固定支撑杆垂直底座于点 , 与是分别可绕点和旋转的调节杆,台灯灯罩可绕点旋转调节光线角度,在调节过程中,最外侧光线、组成的始终保持不变.现调节台灯,使外侧光线 , , 若 , 则( )
A、2 B、2 C、3 D、47. 如图是一盏可调节台灯及其示意图.固定支撑杆垂直底座于点 , 与是分别可绕点和旋转的调节杆,台灯灯罩可绕点旋转调节光线角度,在调节过程中,最外侧光线、组成的始终保持不变.现调节台灯,使外侧光线 , , 若 , 则( ) A、 B、 C、 D、8. 如图,是的直径且 , 点在圆上且 , 的平分线交于点 , 连接并过点作 , 垂足为 , 则弦的长度为( )
A、 B、 C、 D、8. 如图,是的直径且 , 点在圆上且 , 的平分线交于点 , 连接并过点作 , 垂足为 , 则弦的长度为( ) A、 B、 C、4 D、9. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( )
A、 B、 C、4 D、9. 如图,在正方形ABCD中,E,F是对角线AC上的两点,且EF=2AE=2CF,连接DE并延长交AB于点M,连接DF并延长交BC于点N,连接MN,则 ( ) A、 B、 C、1 D、10. 如图,是的内接三角形,若 , , , 则的长为( )
A、 B、 C、1 D、10. 如图,是的内接三角形,若 , , , 则的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(此题共5小题,每小题3分,共15分)
-
11. 分解因式: .12. 某招聘考试分笔试和面试两种,小明笔试成绩90分,面试成绩85分,如果笔试成绩、面试成绩按3:2计算,那么小明的平均成绩是分
13. 某超市以A、B两种糖果为原料,组装出了甲、乙、丙三种糖果礼盒(礼盒包装成本忽略不计).其中,甲礼盒每盒含1千克A糖果、1千克B糖果;乙礼盒每盒含2千克A糖果、1千克B糖果;丙礼盒每盒含1千克A糖果、3千克B糖果.甲礼盒每盒售价48元,利润率为20%.国庆节期间,该超市进行打折促销活动,将甲、乙、丙礼盒各一盒合组装成大礼包,并且每购买一个大礼包可免费赠送一个乙礼盒,这样即可实现利润率为30%,则每个大礼包的售价为元.14. 如图,在平面直角坐标系中,矩形ABCD的顶点A,B在x轴的正半轴上,反比例函数的图象经过顶点D,分别与对角线AC,边BC交于点E,F,连接EF,AF.若点E为AC的中点,△AEF的面积为2,则k的值为.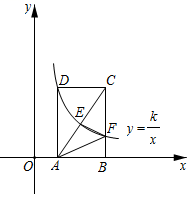 15. 如图,在正方形中,为的中点,为的中点,
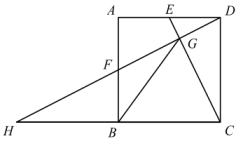
15. 如图,在正方形中,为的中点,为的中点,的延长线与的延长线交于点 , 与相交于点 . 若 , 则的长为 .
三、解答题(共7小题,共55分,其中第16题6分,第17题、第18题7分,第19题、第20题8分,第21题9分,第22题10分)
-
16. 计算:.17. 先化简,再求值: , 其中 .18. 今年3月25日是第29个全国中小学生安全教育日.某市面向中小学生举行了一次关于心理健康、预防欺凌、防溺水、应急疏散等安全专题知识竞赛,共有18000名学生参加本次竞赛.为了解本次竞赛成绩情况,随机抽取了n名学生的成绩x(成绩均为整数,满分为100分)分成四个组:1组(),2组(),3组(),4组(),并绘制如图所示频数分布图.
 (1)、 ;所抽取的n名学生成绩的中位数在第 组;(2)、若成绩在第4组才为优秀,则所抽取的n名学生中成绩为优秀的频率为 ;(3)、试估计18000名参赛学生中,成绩大于或等于70分的人数.19. 根据以下素材,探索完成任务.
(1)、 ;所抽取的n名学生成绩的中位数在第 组;(2)、若成绩在第4组才为优秀,则所抽取的n名学生中成绩为优秀的频率为 ;(3)、试估计18000名参赛学生中,成绩大于或等于70分的人数.19. 根据以下素材,探索完成任务.素材1
某校统一安装了日光灯,日光灯中最易损坏的是灯管和镇流器.
素材2
该校后勤部准备补进灯管和镇流器共400件.批发市场灯管的单价为30元,镇流器的单价为80元.商家为了促销且保证有一定的利润,当镇流器购买数量超过80件时,每多购买1件,单价下降1元,但单价不低于50元.
问题解决
任务1
若镇流器补进90件,则学校补进镇流器和灯管共多少元?
任务2
设镇流器补进x件,若 , 刚补进镇流器的单价为 ▲ 元,补进灯管的总价为 ▲ (用含x的代数式表示);
任务3
若学校后勤部补进镇流器和灯管共花15000元,求补进镇流器多少件?
20. 如图是形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,请在图a、b中分别画出符合要求的图形,所画图形各顶点必须在格点上; (1)、画一个底边长为4,面积为8的等腰三角形;(2)、画一个面积为10的等腰直角三角形.21.根据背景素材,探索解决问题.
(1)、画一个底边长为4,面积为8的等腰三角形;(2)、画一个面积为10的等腰直角三角形.21.根据背景素材,探索解决问题.生活中的数学——自动旋转式洒水喷头如何灌溉草坪
背景素材
数学来源于生活,九4班分四个小组,开展数学项目式实践活动,获取所有数据共享,对草坪喷水管建立数学模型.草坪装有1个自动旋转式洒水喷头,灌溉园林草坪.如图1所示,观察喷头可顺、逆时针往返喷洒.

甲小组在图2中建立合适的直角坐标系,喷水口中心O有一喷水管OA , 从A点向外喷水,喷出的水柱最外层的形状为抛物线.以水平方向为x轴,点O为原点建立平面直角坐标系,点A(喷水口)在y轴上,x轴上的点D为水柱的最外落水点.
乙小组在甲小组基础上,测量得距洒水喷头水平距离较远若干米的E处,正上方有一树枝叶F , 旋转式喷洒水柱外端刚好碰到树叶F的最低处.
丙小组在甲小组基础上,测量得喷水口中心O到水柱的最外落水点D距离为半径,建立⊙O半径为OD的扇形平面图(图3).
问题解决
任务1
获取数据
丁小组测量得喷头的高米,喷水口中心点O到水柱的最外落水点D水平距离为8米,经过点 .
解决问题
求出水柱所在抛物线的函数解析式.
任务2
获取数据
丁小组测树叶F距水平地面最低高度米,点F在抛物线上且离水喷头水平距离较远,E在OD上,OD⊥EF .
解决问题
求OE的长.
任务3
推理计算
丁小组观察自动旋转式洒水喷头可顺、逆时针往返喷洒,可平面旋转角度不超过240°,求:
①这个喷头最多可洒水多少平方米?
②在①条件下,此时DD'的长.
22. 综合与探究在矩形ABCD的CD边上取一点E , 将△BCE沿BE翻折,使点C恰好落在AD边上的点F处.
 (1)、如图①,若BC=2BA , 求∠CBE的度数;(2)、如图②,当AB=5,且AF•FD=10时,求EF的长;(3)、如图③,延长EF , 与∠ABF的角平分线交于点M , BM交AD于点N , 当NF=AN+FD时,请直接写出的值.
(1)、如图①,若BC=2BA , 求∠CBE的度数;(2)、如图②,当AB=5,且AF•FD=10时,求EF的长;(3)、如图③,延长EF , 与∠ABF的角平分线交于点M , BM交AD于点N , 当NF=AN+FD时,请直接写出的值.