浙江省温州市龙港市2024年中考数学二模试题
试卷更新日期:2024-05-23 类型:中考模拟
一、选择题(本题有10小题,每小题3分,共30分.请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)
-
1. 计算:的结果是( )A、 B、 C、1 D、92. 据国家海关总署统计,2024年第一季度进口粮食约38400000吨,数字38400000用科学记数法表示为( )A、 B、 C、 D、3. 如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )
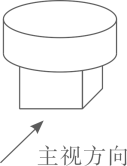 A、
A、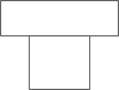 B、
B、 C、
C、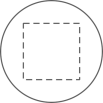 D、
D、 4. 某公司今年月份生产体育器材产量统计图如图所示,已知乙器材的产量为40万件,则丙器材的产量是( )万件
4. 某公司今年月份生产体育器材产量统计图如图所示,已知乙器材的产量为40万件,则丙器材的产量是( )万件 A、40 B、30 C、20 D、105. 下列运算中,正确的是( )A、 B、 C、 D、6. 《九章算术》记载关于“盈不足”的问题:“今有共买金,人出四百,盈三百;人出三百,不足一百.问人数、金价各几何?”这段话的意思是:“今有数人合伙买金子,每人出400钱,会剩余300钱,每人出300钱,会差100钱”若设合伙人有x人,金价y钱,根据题意列出方程组为( )A、 B、 C、 D、7. 图1是某款篮球架,图2是其部分示意图,立柱垂直地面 , 支架与相交于点A,支架交于点G,米,米, , 则立柱的高为( )米
A、40 B、30 C、20 D、105. 下列运算中,正确的是( )A、 B、 C、 D、6. 《九章算术》记载关于“盈不足”的问题:“今有共买金,人出四百,盈三百;人出三百,不足一百.问人数、金价各几何?”这段话的意思是:“今有数人合伙买金子,每人出400钱,会剩余300钱,每人出300钱,会差100钱”若设合伙人有x人,金价y钱,根据题意列出方程组为( )A、 B、 C、 D、7. 图1是某款篮球架,图2是其部分示意图,立柱垂直地面 , 支架与相交于点A,支架交于点G,米,米, , 则立柱的高为( )米 A、 B、 C、 D、8. 如图,点光源O射出的光线沿直线传播,将胶片上的建筑物图片投影到与胶片平行的屏幕上,形成影像 . 已知 , 点光源到胶片的距离长为 , 长为 , 则胶片与屏幕的距离为( )
A、 B、 C、 D、8. 如图,点光源O射出的光线沿直线传播,将胶片上的建筑物图片投影到与胶片平行的屏幕上,形成影像 . 已知 , 点光源到胶片的距离长为 , 长为 , 则胶片与屏幕的距离为( ) A、86 B、84 C、80 D、789. 如图,以为直径的与相切于点B,连结 , 分别交于点E,F,连结 , 记 , , 若 , 则与的关系式为( )
A、86 B、84 C、80 D、789. 如图,以为直径的与相切于点B,连结 , 分别交于点E,F,连结 , 记 , , 若 , 则与的关系式为( ) A、 B、 C、 D、10. 新定义:两边之比等于黄金比的矩形叫做黄金矩形,如图,矩形是黄金矩形(),点E、F分别在边、上,将矩形沿直线折叠,使点B的对应点落在CD边上,点A的对应点为 , 过点E作于点G,当矩形也是黄金矩形()时,则( )
A、 B、 C、 D、10. 新定义:两边之比等于黄金比的矩形叫做黄金矩形,如图,矩形是黄金矩形(),点E、F分别在边、上,将矩形沿直线折叠,使点B的对应点落在CD边上,点A的对应点为 , 过点E作于点G,当矩形也是黄金矩形()时,则( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(本题有6小题,每小题3分,共18分)
-
11. 因式分解: .12. 如表为某中学统计的九年级50名学生体重达标情况(单位:人),在该年级随机抽取一名学生,该生体重“标准”的概率是 .
“偏瘦”
“标准”
“超重”
“肥胖”
8
35
3
4
13. 不等式组的解是 .14. 如图,已知折扇的骨柄 , 折扇张开的最大角度为 , 此时的长度 . (结果保留) 15. 如图,已知点P在直线上,点P的坐标为 , 将点P向下平移a个单位,再向左b平移个单位,得到点 , 且点也在该一次函数上,则 .
15. 如图,已知点P在直线上,点P的坐标为 , 将点P向下平移a个单位,再向左b平移个单位,得到点 , 且点也在该一次函数上,则 . 16. 中国传统玩具不倒翁(如图1),它的主体截面图由两个圆构成(如图2),测得不倒翁的高度 , 上部分小圆半径 , , 求底部大圆半径;当不倒翁翻到如图3所示时,此时点B离地面的距离 , 则点A到地面的距离 .
16. 中国传统玩具不倒翁(如图1),它的主体截面图由两个圆构成(如图2),测得不倒翁的高度 , 上部分小圆半径 , , 求底部大圆半径;当不倒翁翻到如图3所示时,此时点B离地面的距离 , 则点A到地面的距离 .
三、解答题(本题有8小题,共72分.解答需写出必要的文字说明、演算步骤)
-
17. (1)计算:
(2)化简:
18. 如图,于点B,于点D,P是BD上一点,且 , . (1)、求证:;(2)、若 , , 求的长.19. 如图在的方格中有一个格点(顶点都在格点上).
(1)、求证:;(2)、若 , , 求的长.19. 如图在的方格中有一个格点(顶点都在格点上). (1)、在图1中在边上找到点D,使把的面积平分;(2)、在图2中画格点 , 使 .20. 某校进行了“生活中的数学知识竞赛”现从甲班和乙班各随机抽取10名学生.统计这部分学生的竞赛成绩(满分50),并对数据(成绩)讲行了收集、整理,分析(其中成绩大于等于40的视为优秀)
(1)、在图1中在边上找到点D,使把的面积平分;(2)、在图2中画格点 , 使 .20. 某校进行了“生活中的数学知识竞赛”现从甲班和乙班各随机抽取10名学生.统计这部分学生的竞赛成绩(满分50),并对数据(成绩)讲行了收集、整理,分析(其中成绩大于等于40的视为优秀)【收集数据】
甲班10名学生竞赛成绩:9,20,50,30,40,30,40,46,40,35
乙班10名学生竞赛成绩:12,45,20,44,34,43,34,36,37,35
【整理数据】
班级
甲班
1
0
1
3
5
乙班
0
1
1
5
3
【分析数据】
班级
平均数
中位数
众数
优秀率
甲班
34
b
40
乙班
a
c
【解决问题】
根据以上信息,回答下列问题:
(1)、填空: , , ;(2)、请你根据【分析数据】中的信息,判断哪个班成绩比较好,并简要说明理由;(3)、学校要求成绩达到45分及以上的同学(甲班2名,乙班1名)要做学习心得分享,王老师随机从这些同学中选取两名同学,请利用树状图或列表法的方法,求选到乙班同学的概率是多少?21. 如图已知反比例函数与一次函数交于点A,B,点A在点B的左侧,点A的横坐标为1. (1)、求反比例函数的表达式;(2)、求出当时,x的取值范围.22. 如图,在中,E、F为对角线的三等分点,延长 , 分别交 , 于点G,H.
(1)、求反比例函数的表达式;(2)、求出当时,x的取值范围.22. 如图,在中,E、F为对角线的三等分点,延长 , 分别交 , 于点G,H. (1)、求证:;(2)、若 , , , 求四边形的面积.23. 综合与实践
(1)、求证:;(2)、若 , , , 求四边形的面积.23. 综合与实践素材1:一年一度的科技节即将到来,小明所在的科技小组研制了一种航模飞机.通过多次实验,收集了飞机的水平飞行距离x(单位:)与相对应的飞行高度y(单位:)的数据(如下表)
飞行水平距离x(单位:)
0
20
40
60
80
100
飞行高度y(单位:)
0
40
64
72
64
40
素材2:如图,活动小组在水平安全线上A处设置一个高度可以变化的发射平台试飞航模飞机

链接:已知航模的飞行高度y(单位:)与水平飞行距离x(单位:)满足二次函数关系
任务1:请求出y关于x的函数关系式(不用写自变量的取值范围),并求出航模的最远飞行距离.
任务2:在安全线上设置回收区域,点M的右侧为回收区域(包括端点M), . 若飞机落到回收区域内,求发射平台相对于安全线的最低高度.
24. 如图1, , 是的两条弦,平分 , 连接 , 且半径 , . (1)、求证:;(2)、求的值;(3)、如图2,连接 , 点Q为边上一动点,延长交于点P.
(1)、求证:;(2)、求的值;(3)、如图2,连接 , 点Q为边上一动点,延长交于点P.①连接 , 若平行三边其中一边时,求的长;
②当点Q从A到C的运动过程中,是否存在最大值?若存在,请求出最大值,若不存在,请说明理由.