2024年广东省深圳市中考数学全真模拟试卷(五)
试卷更新日期:2024-05-28 类型:中考模拟
一、选择题(本大题共10题,每小题3分,共30分,每小题有四个选项,只有一个选项正确)
-
1. 下列图形中可由其中的部分图形经过平移得到的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各数中,最大的是( )A、-3 B、0 C、2 D、|-1|3. 下列运算正确的是( )A、 B、 C、 D、4. 为了调查我市某校学生的视力情况,在全校的2000名学生中随机抽取了300名学生,下列说法正确的是( )A、此次调查属于全面调查 B、样本容量是300 C、2000名学生是总体 D、被抽取的每一名学生称为个体5. 已知关于x的不等式组有四个整数解,则m的取值范围是( )A、 B、 C、 D、6. 古代数学趣题:老头提篮去赶集,一共花去七十七;满满装了一菜篮,十斤大肉三斤鱼;买好未曾问单价,只因回家心里急;道旁行人告诉他,九斤肉钱五斤鱼.意思是:77元钱共买了10斤肉和3斤鱼,9斤肉的钱等于5斤鱼的钱,问每斤肉和鱼各是多少钱?设每斤肉元,每斤鱼元,可列方程组为( )A、 B、 C、 D、7. 如图,将一个形状的楔子从木桩的底端点P沿水平方向打入木桩底下,可以使木桩向上运动.若楔子斜面的倾斜角为 , 楔子沿水平方向前进5厘米,则木桩上升( )
2. 下列各数中,最大的是( )A、-3 B、0 C、2 D、|-1|3. 下列运算正确的是( )A、 B、 C、 D、4. 为了调查我市某校学生的视力情况,在全校的2000名学生中随机抽取了300名学生,下列说法正确的是( )A、此次调查属于全面调查 B、样本容量是300 C、2000名学生是总体 D、被抽取的每一名学生称为个体5. 已知关于x的不等式组有四个整数解,则m的取值范围是( )A、 B、 C、 D、6. 古代数学趣题:老头提篮去赶集,一共花去七十七;满满装了一菜篮,十斤大肉三斤鱼;买好未曾问单价,只因回家心里急;道旁行人告诉他,九斤肉钱五斤鱼.意思是:77元钱共买了10斤肉和3斤鱼,9斤肉的钱等于5斤鱼的钱,问每斤肉和鱼各是多少钱?设每斤肉元,每斤鱼元,可列方程组为( )A、 B、 C、 D、7. 如图,将一个形状的楔子从木桩的底端点P沿水平方向打入木桩底下,可以使木桩向上运动.若楔子斜面的倾斜角为 , 楔子沿水平方向前进5厘米,则木桩上升( ) A、厘米 B、厘米 C、厘米 D、厘米8. 如图,有一个半径为2的圆形时钟,其中每个刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )
A、厘米 B、厘米 C、厘米 D、厘米8. 如图,有一个半径为2的圆形时钟,其中每个刻度间的弧长均相等,过9点和11点的位置作一条线段,则钟面中阴影部分的面积为( )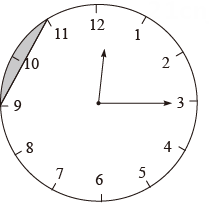 A、 B、 C、 D、9. 如图,在中, , 平分交于点D , 平分交于点E , , 交于点F . 则下列说法正确的有( )
A、 B、 C、 D、9. 如图,在中, , 平分交于点D , 平分交于点E , , 交于点F . 则下列说法正确的有( )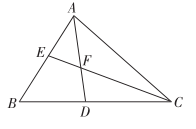
①;②;③若 , 则;④ .
A、1个 B、2个 C、3个 D、4个二、填空题(本题共5题,每题3分,共15分)
-
10. 因式分解: .11. 的两根分别为、 , 则 .12. “孔子周游列国”是流传很广的故事.有一次孔子和学生们到距离他们住的驿站15公里的书院参观,学生们步行出发,1小时后,孔子乘牛车出发,牛车的速度是步行的速度的1.5倍,若孔子和学生们同时到达书院,设学生们步行的速度为每小时公里,则可列方程.13. 如图,已知点点在反比例函数 的函数图象上, , 则的值为 .
 14. 如图,在Rt△ABC中,∠ABC=90°,边AC的垂直平分线DE交BC于点D , 交AC于点E , BF⊥AC于点F , 连接AD交BF于点G . 若BC=6, , 则DE的长为 .
14. 如图,在Rt△ABC中,∠ABC=90°,边AC的垂直平分线DE交BC于点D , 交AC于点E , BF⊥AC于点F , 连接AD交BF于点G . 若BC=6, , 则DE的长为 . ,
, 三、解答题(本题共7题,其中第16题6分,第17题7分,第18题8分,第19题7分,第20题8分,第21题9分,第22题10分)
-
15. 计算:16. 先化简,再求值: ,其中 .17. 某校加强了1分钟定时跳绳的训练后,抽样调查部分学生的“1分钟跳绳”成绩,并绘制了不完整的频数分布直方图和扇形图(如图).根据图中提供的信息解决下列问题:

A:
B:
C:
D:
E:
(1)、抽样的人数是人,扇形中;(2)、抽样中D组人数是 ▲ 人,本次抽取的部分学生“1分钟跳绳”成绩组成的一组数据的中位数落在 ▲ 组(填),并补全频数分布直方图;(3)、如果“1分钟跳绳”成绩大于等于160次为满分,那么该校2100名学生中“1分钟跳绳”成绩为满分的大约有多少人?18. 如图,在中, , . (1)、实践与操作:用尺规作图法作线段的垂直平分线,交于点D , 交于点E(保留作图痕迹,不要求写作法);(2)、应用与计算:在(1)的条件下,连接 , 若 , 求的长.19. 某蔬菜种植基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.
(1)、实践与操作:用尺规作图法作线段的垂直平分线,交于点D , 交于点E(保留作图痕迹,不要求写作法);(2)、应用与计算:在(1)的条件下,连接 , 若 , 求的长.19. 某蔬菜种植基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.(1)改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元?
(2)已知改造1个甲种型号大棚的时间是5天,改造1个乙种型号大概的时间是3天,该基地计划改造甲、乙两种蔬菜大棚共8个,改造资金最多能投入128万元,要求改造时间不超过35天,请问有几种改造方案?哪种方案基地投入资金最少,最少是多少?
20. 根据以下素材,探索完成任务.如何设计喷泉安全通道?
在抛物线形的喷泉水柱下设置一条安全的通道,可以让儿童在任意时间穿过安全通道时不被水柱喷到(穿梭过程中人的高度变化忽略不计).
素材1
图1为音乐喷泉,喷头的高度在垂直地面的方向上随着音乐变化而上下移动.不同高度的喷头喷出来的水呈抛物线型或抛物线的一部分,但形状相同,最高高度也相同,水落地点都在喷水管的右侧.

素材2
图2是当喷水头在地面上时(喷水头最低),其抛物线形水柱的示意图,水落地点离喷水口的距离为 , 水柱最高点离地面 .
图3是某一时刻时,水柱形状的示意图.为喷水管,为水的落地点,记长度为喷泉跨度.


素材3
安全通道在线段上,若无论喷头高度如何变化,水柱都不会进入上方的矩形区域,则称这个矩形区域为安全区域.

问题解决
任务1
确定喷泉形状.
在图2中,以为原点,所在直线为轴,建立平面直角坐
标系,求出抛物线的函数表达式.
任务2
确定喷泉跨度的最小值.
若喷水管最高可伸长到 , 求出喷泉跨度的最小值.
任务3
设计通道位置及儿童的身高上限.
现在需要一条宽为的安全通道 , 为了确保进入安全通道
上的任何人都能在安全区域内,则能够进入该安全通道的人
的最大身高为多少?(精确到)
21. 在正方形中,点是对角线上的一点,且 , 将线段绕着点顺时针旋转至 , 记旋转角为 , 连接、 , 并以为斜边在其上方作 , 连接 . (1)、特例探究:如图1,当 , 时,线段与的数量关系为;(2)、问题探究:如图2所示,在旋转的过程中,
(1)、特例探究:如图1,当 , 时,线段与的数量关系为;(2)、问题探究:如图2所示,在旋转的过程中,①(1)中的结论是否依然成立,若成立,请说明理由;
②当 , 时,若 , 求的长度;
(3)、拓展提升:若正方形改为矩形 , 且 , 其它条件不变,在旋转的过程中,当、、三点共线时,如图3所示,若 , , 直接写出的长度.(用含的式子表示)