2024年广东省深圳市中考数学全真模拟试卷(四)
试卷更新日期:2024-05-27 类型:中考模拟
一、选择题(本大题共10小题,每题3分,共30分,每个题题有四个选项,只有一个是正确的)
-
1. 某种冠状病毒的大小约为0.000125mm,该数用科学记数法表示正确的是( )A、0.125×10﹣3 B、0.125×10﹣4 C、1.25×10﹣3 D、1.25×10﹣42. 下列各组数中,互为相反数的是( )A、 与 B、 与 C、 与 D、 与3. 若点在第一象限,则的取值范围在数轴上表示为( )A、
 B、
B、 C、
C、 D、
D、 4. 为了落实“双减”政策,进一步丰富文体活动,学校准备购进一批篮球和足球,已知每个篮球的价格比每个足球的价格多20元,用1500元购进篮球的数量比用800元购进足球的数量多5个,如果设每个足球的价格为x元,那么可列方程为( )A、 B、 C、 D、5. 中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大雪”,其中既是轴对称图形,又是中心对称图形的是( )A、
4. 为了落实“双减”政策,进一步丰富文体活动,学校准备购进一批篮球和足球,已知每个篮球的价格比每个足球的价格多20元,用1500元购进篮球的数量比用800元购进足球的数量多5个,如果设每个足球的价格为x元,那么可列方程为( )A、 B、 C、 D、5. 中国“二十四节气”已被列入联合国教科文组织人类非物质文化遗产代表作名录,下列四幅作品分别代表“立春”、“立夏”、“芒种”、“大雪”,其中既是轴对称图形,又是中心对称图形的是( )A、 B、
B、 C、
C、 D、
D、 6. 一组数据2,2,2,3,5,8,13,若加入一个数a,一定不会发生变化的统计量是( )A、方差 B、平均数 C、中位数 D、众数
6. 一组数据2,2,2,3,5,8,13,若加入一个数a,一定不会发生变化的统计量是( )A、方差 B、平均数 C、中位数 D、众数二、填空题(本题有5小题,每题3分,共15分)
-
7. 因式分解: .8. 如图,三角形纸片中, , , , 折叠这个三角形,使点B落在的中点D处,折痕为 , 那么的长为 .
 9. 如图,点A、B在反比例函数的图象上,轴,垂足为D , . 若四边形的面积为6, , 则k的值为 .
9. 如图,点A、B在反比例函数的图象上,轴,垂足为D , . 若四边形的面积为6, , 则k的值为 .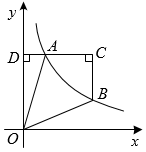 10. 如图,在中,点为的中点, , , , 则边上的高为 .
10. 如图,在中,点为的中点, , , , 则边上的高为 .
三、解答题(本题共7小题,其中第16题6分,第17题7分,第18题7分,第19题8分,第20题8分,第21题9分,第22题10分),共55分
-
11. 先化简,再求值: ,其中 .12. 图1,图2都是由边长为1的小等边三角形构成的网格,每个小等边三角形的顶点称为格点,线段AB的端点均在格点上,分别按要求画出图形.
 (1)、在图1中画出一个以AB为边的口ABCD,且点C和点D均在格点上;(2)、在图2中画出一个以AB为对角线的菱形AEBF,且点E和点F均在格点上.13. 我县组织开展研学活动,共有月岩,陈树湘烈士纪念馆,濂溪故里,葫芦岩红军渡4个地点可供选择,让同学们投票决定最终研学地点,现将同学们的投票结果制成如下统计图(其中A:月岩,B:陈树湘烈士纪念馆,C:濂溪故里,D:葫芦岩红军渡),根据相关信息,回答下列问题:
(1)、在图1中画出一个以AB为边的口ABCD,且点C和点D均在格点上;(2)、在图2中画出一个以AB为对角线的菱形AEBF,且点E和点F均在格点上.13. 我县组织开展研学活动,共有月岩,陈树湘烈士纪念馆,濂溪故里,葫芦岩红军渡4个地点可供选择,让同学们投票决定最终研学地点,现将同学们的投票结果制成如下统计图(其中A:月岩,B:陈树湘烈士纪念馆,C:濂溪故里,D:葫芦岩红军渡),根据相关信息,回答下列问题:
 (1)、本次抽样的样本容量为 , 请补全条形统计图;(2)、扇形统计图中a的值为 , 圆心角β的度数为;(3)、若我县有5000名同学参加研学活动,试估计去月岩的有多少?14. 某中学为了创建良好的校园读书环境,去年购买了一批图书.其中故事书的单价比文学书的单价多4元,用1200元购买的故事书与用800元购买的文学书数量相等.(1)、求去年购买的文学书和故事书的单价各是多少元?(2)、若今年文学书的单价比去年提高了25%,故事书的单价与去年相同,这所中学今年计划再购买文学书和故事书共200本,且购买文学书和故事书的总费用不超过2120元,这所中学今年至少要购买多少本文学书?15. 过山车是倍受年轻人喜爱的经典娱乐项目.如图14,为过山车的一部分轨道(B为轨道与地面的交点,图中的x轴表示地面),它可以看成抛物线的一部分,其中米(轨道厚度忽略不计).
(1)、本次抽样的样本容量为 , 请补全条形统计图;(2)、扇形统计图中a的值为 , 圆心角β的度数为;(3)、若我县有5000名同学参加研学活动,试估计去月岩的有多少?14. 某中学为了创建良好的校园读书环境,去年购买了一批图书.其中故事书的单价比文学书的单价多4元,用1200元购买的故事书与用800元购买的文学书数量相等.(1)、求去年购买的文学书和故事书的单价各是多少元?(2)、若今年文学书的单价比去年提高了25%,故事书的单价与去年相同,这所中学今年计划再购买文学书和故事书共200本,且购买文学书和故事书的总费用不超过2120元,这所中学今年至少要购买多少本文学书?15. 过山车是倍受年轻人喜爱的经典娱乐项目.如图14,为过山车的一部分轨道(B为轨道与地面的交点,图中的x轴表示地面),它可以看成抛物线的一部分,其中米(轨道厚度忽略不计). (1)、写出a , b之间的数量关系;(2)、已知米.
(1)、写出a , b之间的数量关系;(2)、已知米.①求抛物线的解析式;
②在轨道距离地面32米处有两个位置M和C , 当过山车运动到点C处时,沿着平行于地面的轨道向前运动了18米至点G , 又进入下坡段(G接口处轨道忽略不计,点H为轨道与地面的交点).已知轨道抛物线的形状与抛物线的形状相同,求的长度;
③现需要在轨道下坡段进行一种安全加固,建造某种材料的水平和竖直支架 , , 且要求 , 如图所示,已知这种材料的价格是5000元/米.当PE的长度为多少时会使造价最低?并求最低造价为多少元?
16. 如图①,在正方形ABCD中,点E , F分别在边AB、BC上,DF⊥CE于点O , 点G , H分别在边AD、BC上,GH⊥CE . (1)、问题解决:①写出DF与CE的数量关系:;
(1)、问题解决:①写出DF与CE的数量关系:;②的值为 ;
(2)、类比探究,如图②,在矩形ABCD中,(k为常数),将矩形ABCD沿GH折叠,使点C落在AB边上的点E处,得到四边形EFGH交AD于点P , 连接CE交GH于点O . 试探究GH与CE之间的数量关系,并说明理由;(3)、拓展应用,如图③,四边形ABCD中,∠BAD=90°,AB=BC=6,AD=CD=4,BF⊥CE , 点E、F分别在边AB、AD上,求的值.