江苏省常州市金坛区2024年中考数学二模试题

试卷更新日期：2024-05-27 类型：中考模拟

进入出卷网下载

一、选择题（本大题共8小题，每小题2分，共16分．在每小题所给出的四个选项中，只有一项是正确的）

1. 如果向东走 $10 m$ 记作 $+ 10 m$ ，那么向西走 $8 m$ 记作（）

A、 $- 10 m$ B、 $+ 10 m$ C、 $+ 8 m$ D、 $- 8 m$

查看试题解析
2. 计算 $2 a - a$ 的结果是（）

A、a B、 $- a$ C、3a D、1

查看试题解析
3. 某几何体的三视图如图所示，则该几何体是（）

A、圆柱 B、圆锥 C、长方体 D、三棱柱

查看试题解析
4. 下列运算正确的是（）

A、 $(a - b) (a + b) = a^{2} + b^{2}$ B、 $(- m + 2) (- m - 2) = m^{2} - 4$ C、 ${(a - b)}^{2} = a^{2} - b^{2}$ D、 ${(a + b)}^{2} = a^{2} + b^{2}$

查看试题解析
5. 元朝朱世杰所著的《算学启蒙》中，记载了这样一道题：良马日行二百四十里，驽马日行一百五十里，驽马先行一十二日，问良马几何日追及之？其大意如下：快马每天行240里，慢马每天行150里，慢马先行12天，快马几天可追上慢马？若设快马x天可追上慢马，可列出方程（）

A、 $\frac{x}{240} = \frac{x}{150} - 12$ B、 $\frac{x}{240} = \frac{x + 12}{150}$ C、 $240 x = 150 (x + 12)$ D、 $240 (x - 12) = 150 x$

查看试题解析
6. 如图，直线CD、EF被OA、OB所截， $C D ∥ E F$ ．若 $∠ 1 = 108 °$ ，则 $∠ 2$ 的度数是（）

A、 $52 °$ B、 $62 °$ C、 $72 °$ D、 $82 °$

查看试题解析
7. 四边形ABCD的边长如图所示，对角线AC的长度随四边形ABCD形状的改变而变化．当 $△ A B C$ 为等腰三角形时，对角线AC的长是（）

A、2 B、3 C、4 D、5

查看试题解析
8. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图像过点 $(- 1, 0)$ ，抛物线的对称轴是直线 $x = 1$ ，顶点在第一象限，给出下列结论：① $a b < 0$ ；② $4 a + 2 b + c > 0$ ；③ $3 a + c > 0$ ；④若 $A (x_{1}, y_{1})$ 、 $B (x_{2}, y_{2})$ （其中 $x_{1} < x_{2}$ ）是抛物线上的两点，且 $x_{1} + x_{2} = 2$ ，则 $y_{1} = y_{2}$ ．其中，错误的结论是（）

A、① B、② C、③ D、④

查看试题解析

二、填空题（本大题共10小题，每小题2分，共20分．不需写出解答过程，请把答案直接写在答题卡相应位置上）

9. 如图，在数轴上，点A表示 $\sqrt{3}$ ，点B与点A位于原点的两侧，且到原点的距离相等，则点B表示的数是．

查看试题解析
10. 计算：（xy²）²= ．

查看试题解析
11. 若 $a + 2 b = 2$ ，则 $2 a + 4 b =$ ．

查看试题解析
12. 因式分解： $m x^{2} - 4 m y^{2} =$ ．

查看试题解析
13. 如图，在 $R t △ A B C$ 中，D是斜边BC的中点，连接AD，若 $A B = 5$ ， $A D = 6.5$ ，则 $A C =$ ．

查看试题解析
14. 如图，在矩形ABCD中， $A B = 2 B C = 4$ ，将线段AB绕点A逆时针方向旋转，使得点B落在边CD上的点E处，则 $\overset{⌢}{B E}$ 的长是．

查看试题解析
15. 如图，AD是 $⊙ O$ 的直径，AB是 $⊙ O$ 的弦，BC与 $⊙ O$ 相切于点B，连接OB．若 $∠ A B C = 65 °$ ，则 $∠ B O D =$ ．

查看试题解析
16. 如图，E是 $▱ A B C D$ 边AB上一点，连接AC、DE交于点F， $\frac{A E}{E B} = \frac{2}{3}$ ，则 $\frac{S_{△ A E F}}{S_{△ C D F}} =$ ．

查看试题解析
17. 如图，在平面直角坐标系中，点A、B在函数 $y = \frac{k}{x}$ （ $k > 0$ ， $x > 0$ ）的图像上，分别以点A、B为圆心，2为半径作圆， $⊙ A$ 与y轴相切、 $⊙ B$ 与x轴相切，连接AB，若 $A B = 4 \sqrt{2}$ ，则 $k =$ ．

查看试题解析
18. 如图，矩形纸片ABCD，E是边CD上一点，连接AE、BE．F是边AD上一个动点，连接BF，沿直线BF将 $△ A B F$ 翻折，点A落在 $△ A B E$ 内部的点G处．若 $A B = \frac{7}{2}$ ， $B C = 4$ ， $D E = \frac{1}{2}$ ，则AF的取值范围是．

查看试题解析

三、解答题（本大题共10小题，共84分．请在答题卡指定区域内作答，如无特殊说明，解答应写出文字说明、演算步骤或推理过程）

19. 计算： ${(\sqrt{3})}^{0} - \sqrt{12} - {(\frac{1}{2})}^{- 1} + | \sqrt{3} + 1 |$ ．

查看试题解析
20. 解方程和不等式组：

(1)、 $\frac{1}{x - 1} + 1 = \frac{3}{2 x - 2}$ ；

(2)、 ${\begin{cases} 2 x + 1 > 0 \\ \frac{x - 1}{3} > x - 1 \end{cases}$

查看试题解析
21. 为增强学生的社会实践能力，促进学生全面发展，某校计划建立小记者站，有 $20$ 名学生报名参加选拔 $.$ 报名的学生需参加采访、写作、摄影三项测试，每项测试均由七位评委打分 $($ 满分 $100$ 分 $)$ ，取平均分作为该项的测试成绩，再将采访、写作、摄影三项的测试成绩按 $4$ ： $4$ ： $2$ 的比例计算出每人的总评成绩．

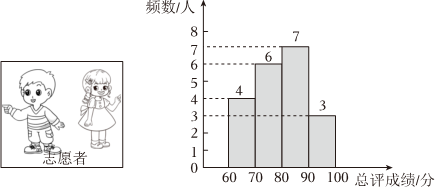
小悦、小涵的三项测试成绩和总评成绩如表，这 $20$ 名学生的总评成绩频数分布直方图 $($ 每组含最小值，不含最大值 $)$ 如图．
选手
测试成绩 $/$ 分
总评成绩 $/$ 分
采访
写作
摄影
小悦
$83$
$72$
$80$
$78$
小涵
$86$
$84$
$▲$
$▲$

(1)、在摄影测试中，七位评委给小涵打出的分数如下： $67$ ， $72$ ， $68$ ， $69$ ， $74$ ， $69$ ， $71 .$ 这组数据的中位数是分，众数是分，平均数是分；

(2)、请你计算小涵的总评成绩；

(3)、学校决定根据总评成绩择优选拔 $12$ 名小记者 $.$ 试分析小悦、小涵能否入选，并说明理由．

查看试题解析
22. 为落实“双减”政策要求，丰富学生课余生活，某校七年级根据学生需求，组建了四个社团供学生选择：A（合唱社团）、B（硬笔书法社团）、C（面点社团）D（街舞社团）．学生从中任意选择两个社团参加活动．

(1)、小明对这4个社团都很感兴趣，如果他随机选择1个社团，他选中D（街舞社团）的概率是；

(2)、小宇和小江在选择过程中，首先都选了社团D（街舞社团），他俩决定各自随机选择第2个社团，请用列表法或树状图求他俩在选第2个社团中选到相同社团的概率．

查看试题解析
23. 如图，在 $△ A B C$ 中， $A B = A C$ ， AD为 $△ A B C$ 的角平分线，以点A为圆心，AD长为半径画弧，与AB、AC分别交于点E、F，连接DE、DF．

(1)、求证： $D E = D F$ ；

(2)、若 $∠ B A C = 80 °$ ，求 $∠ C D F$ 的度数．

查看试题解析
24. 如图，一次函数 $y = m x + n$ 的图像与y轴负半轴交于点A，与反比例函数 $y = \frac{k}{x} (x > 0)$ 的图像交于点 $B (3, 2)$ ．

(1)、求反比例函数的表达式；

(2)、连接OB，当 $△ O A B$ 的面积为3时，求一次函数的表达式．

查看试题解析
25. 如图，学校为美化校园环境，打造绿色校园，决定用60米长的篱笆围成一个一面靠墙（墙足够长）的长方形花园，并用一道篱笆把花园分为A、B两块长方形区域．

(1)、设垂直于墙的篱笆长是 $x m$ ，花园面积是 $S m^{2}$ ，写出S关于x的函数表达式，并求S的最大值；

(2)、在花园面积最大的条件下，A、B两块区域内分别种植牡丹和芍药，每平方米种植2株，若A区域面积不小于B区域面积的2倍，则至少要购买多少株牡丹？

查看试题解析
26. 给出如下定义：点 $P (x_{1}, y_{1})$ ，点 $Q (x_{2}, y_{2})$ 是平面直角坐标系xOy中不同的两点，且 $x_{1} \neq x_{2}$ ，若存在一个正数k，使点P、Q的坐标满足 $| y_{2} - y_{1} | = k | x_{2} - x_{1} |$ ，则称P、Q为一对“斜关点”，k叫点P、Q的“斜关比”，记作 $k (P, Q)$ ．由定义可知， $k (P, Q) = k (Q, P)$ ．例如：若 $P (1, 0)$ ， $Q (3, \frac{1}{2})$ ，有 $| \frac{1}{2} - 0 | = \frac{1}{4} | 3 - 1 |$ ，所以点P、Q为一对“斜关点”，且“斜关比”为 $\frac{1}{4}$ ．
如图，已知平面直角坐标系xOy中，点 $A (1, 0)$ 、 $B (3, 1)$ 、 $C (3, 0)$ 、 $D (3, - 3)$ ．

(1)、在点A、B、C、D中，写出一对“斜关点”是，此两点的“斜关比”是（只需写出一对即可）．

(2)、若存在点E，使得点A、E是一对“斜关点”，点C、E也是一对“斜关点”，且 $k (A, E) = k (C, E) = 2$ ，求点E的坐标．

(3)、若 $⊙ O$ 的半径是4，M是 $⊙ O$ 上一点，满足 $M T = 1$ 的所有点T，都与点D是一对“斜关点”，且 $k (T, D) \geq 1$ ．请直接写出点M横坐标m的取值范围．

查看试题解析
27. 如图，在 $R t △ A B C$ 中， $∠ A C B = 90 °$ ，将线段BC绕点B按顺时针方向旋转到BD，连接CD．点F是边AB上一个动点，连接DF交BC于点E．已知 $B C = 2$ ， $∠ D C B - ∠ A B C = 45 °$ ．

(1)、若 $∠ C A B = 70 °$ ，则 $∠ A B D =$ ；

(2)、若 $∠ C B A = 27 °$ ， $D C = D E$ ，求CD的长；

(3)、若 $D F ⊥ A B$ ，点E是BC的中点，求AC的长．

查看试题解析
28. 如图，在平面直角坐标系xOy中，二次函数 $y = x^{2} + b x + 4$ 的图像与x轴正半轴交于点A、B，与y轴交于点C， $O C = 4 O A$ ，点P是线段BC上一点（不与点B、C重合），过点P作 $P Q ⊥ x$ 轴，交抛物线于点Q，连接OQ，四边形OCPQ是平行四边形．

(1)、填空： $b =$ ．

(2)、求四边形OCPQ的面积；

(3)、若点D是OC的中点，连接AD、AC．点 $E (5, 4)$ 是抛物线上一点，F是直线QE上一点，连接BE、BF若 $△ B E F$ 与 $△ A D C$ 相似，求点F的坐标．

查看试题解析

选手	测试成绩 $/$ 分			总评成绩 $/$ 分
选手	采访	写作	摄影	总评成绩 $/$ 分
小悦	$83$	$72$	$80$	$78$
小涵	$86$	$84$	$▲$	$▲$