湖北省恩施市沙地、崔坝、双河、新塘四校2023-2024学年七年级下学期数学期中联考试题

试卷更新日期：2024-05-27 类型：期中考试

进入出卷网下载

一、选择题（共10题，每题3分，共30分．每题只有一个选项符合题目要求）

1. 实数9的平方根为（）

A、3 B、 $\sqrt{3}$ C、 $\pm \sqrt{3}$ D、 $\pm 3$

查看试题解析
2. 在实数 $- \sqrt{2}$ ， $0.31$ ， $\frac{π}{3}$ ， $0.1010010001$ ， $\sqrt{8}$ 中，无理数有（　　）个

A、1 B、2 C、3 D、4

查看试题解析
3. 下列图形中，由∠1=∠2能得到AB∥CD的是（）

A、 B、 C、 D、

查看试题解析
4. 如图，一把长方形直尺沿直线断开并错位，点E、D、B、F在同一条直线上，若∠ADE=125°，则∠DBC的度数为（）

A、55° B、65° C、75° D、125°

查看试题解析
5. 交换下列命题的题设和结论，得到的新命题是假命题的是(　　)

A、两直线平行，同位角相等 B、相等的角是对顶角 C、所有的直角都是相等的 D、若a=b，则a﹣3=b﹣3

查看试题解析
6.
如图，直线AB∥CD，一个含60°角的直角三角板EFG（∠E=60°）的直角顶点F在直线AB上，斜边EG与AB相交于点H，CD与FG相交于点M．若∠AHG=50°，则∠FMD等于（　　）

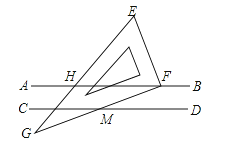A、10° B、20° C、30° D、50°

查看试题解析
7. 如图，A，B，C，D中的哪幅图案可以通过图案①平移得到（　　）

A、 B、 C、 D、

查看试题解析
8. 下列各式正确的是（）

A、 $\pm \sqrt[3]{1} = \pm 1$ B、 $\sqrt{4} = \pm 2$ C、 $- \sqrt{(- 6)^{2}} = 6$ D、 $\sqrt[3]{- 27} = 3$

查看试题解析
9. 如图，把一张长方形纸条ABCD沿EF折叠，若∠1=56°，则∠FGE应的( )

A、68° B、34° C、56° D、不能确定

查看试题解析
10. 如图， $a / / b$ ， M ， N分别在a ， b上，P为两平行线间一点，那么 $∠ 1 + ∠ 2 + ∠ 3 =$ （）

A、 $180 °$ B、 $270 °$ C、 $360 °$ D、 $540 °$

查看试题解析

二、填空题（共5题，每题3分，共15分）

11. 实数 $- \sqrt{2}$ 的绝对值是．

查看试题解析
12. 若 $2 n - 5$ 与 $n - 1$ 是正数 $x$ 的两个平方根，则 $x =$ ．

查看试题解析
13. 如图，直线AB、CD相交于点O，OM⊥AB于点O，若∠MOD=43°，则∠COB=度．

查看试题解析
14. 如图，将三角形 $A B C$ 沿 $B C$ 向右平移得到三角形 $D E F$ ，若 $B C = 5, E C = 3$ ，则 $C F$ 的长是．

查看试题解析
15. 在草稿纸上计算：① $\sqrt{1^{3}}$ ；② $\sqrt{1^{3} + 2^{3}}$ ；③ $\sqrt{1^{3} + 2^{3} + 3^{3}}$ ；④ $\sqrt{1^{3} + 2^{3} + 3^{3} + 4^{3}}$ ，观察你计算的结果，用你发现的规律直接写出下面式子的值 $\sqrt{1^{3} + 2^{3} + 3^{3} + \cdot \cdot \cdot + 28^{3}}$ = ．

查看试题解析

三、解答题（共9题，共75分，解答应写出文字说明，证明过程或演算步骤）

16.

(1)、计算： $\sqrt[3]{- 27} + | - 3 |$

(2)、求 $x$ 的值： $3 x^{2} = 27$

查看试题解析
17. 一个角的补角等于它的余角的3倍，求这个角的度数．

查看试题解析
18. 如图， $E$ 点为 $D F$ 上的点， $B$ 为 $A C$ 上的点， $∠ 1 = ∠ 2$ ， $∠ C = ∠ D$ ，那么 $D F ∥ A C$ ，请完成以下证明过程（在括号内要写出相应的几何依据）
证明： $∵ ∠ 1 = ∠ 2$ ， $∠ 2 = ∠ 3$ ， $∠ 1 = ∠ 4$ ，
$∴ ∠ 3 = ∠ 4$
∴_▲_ $∥$ _▲_（_▲_）
$∴ ∠ C = ∠ A B D$ （_▲_）
$∵ ∠ C = ∠ D$
$∴ ∠ D = ∠ A B D$ （_▲_）
$∴ D F ∥ A C$ （_▲_）

查看试题解析
19. 如图，已知： $A E$ 平分 $∠ B A C, C E$ 平分 $∠ A C D$ ，且 $A B ∥ C D$ ．
求证： $∠ E = 90 °$

查看试题解析
20. 已知 $\sqrt{36} = x, \sqrt{y} = 3, z$ 是 $- 27$ 的立方根，求： $2 x + y - 5 z$ 的值．

查看试题解析
21. 如图， $△ A B C$ 的三个顶点都在正方形网格的格点上（网格中每个小正方形的边长都为1个单位长度），将 $△ A B C$ 平移，使点 $A$ 到 $A_{1}$ 的位置.

(1)、画出平移后的 $△ A_{1} B_{1} C_{1}$ ；

(2)、连接 $A A_{1}$ 、 $B B_{1}$ ，则线段 $A A_{1}$ 与 $B B_{1}$ 的关系是；

(3)、求 $△ A_{1} B_{1} C_{1}$ 的面积.

查看试题解析
22. 如图，已知 $∠ 1 + ∠ 2 = 180 °$ ， $∠ D E F = ∠ A$ ，
求证：

(1)、 $E F ∥ A B$ .

(2)、 $∠ A C B = ∠ D E B$ .

查看试题解析
23. 如图， $A B ∥ C D$ ，连接 $C A$ 并延长至点 $H$ ， $C F$ 平分 $∠ A C D$ ， $C E ⊥ C F$ ， $∠ G A H + ∠ A F C = 90 °$ ．

(1)、求证 $A G ∥ C E$ ；

(2)、若 $∠ G A F = 120 °$ ，求 $∠ A F C$ 的度数．

查看试题解析
24. 已知：直线EF分别与直线AB，CD相交于点G，H，并且∠AGE+∠DHE＝180°．

(1)、如图1，求证：AB∥CD；

(2)、如图2，点M在直线AB，CD之间，连接GM，HM，求证：∠M＝∠AGM+∠CHM；

(3)、如图3，在（2）的条件下，射线GH是∠BGM的平分线，在MH的延长线上取点N，连接GN，若∠N＝∠AGM，∠M＝∠N+ $\frac{1}{2}$ ∠FGN，求∠MHG的度数．

查看试题解析