广西河池市2023-2024学年八年级下学期数学期中考试试卷

试卷更新日期：2024-05-27 类型：期中考试

进入出卷网下载

一、选择题（共12小题，每小题3分，共36分．在每小题给出的四个选项中只有一项是符合要求的，用2B铅笔把答题卡上对应题目的答案标号涂黑．）

1. 下列式子中，是二次根式的是（）

A、 $π$ B、 $\frac{1}{3}$ C、 $\sqrt{- 2}$ D、 $\sqrt{2}$

查看试题解析
2. 如图，体育课上测量跳远成绩的依据是（）

A、平行线间的距离相等 B、垂线段最短 C、两点之间，线段最短 D、两点确定一条直线

查看试题解析
3. 与 $\sqrt{4 \times 9}$ 的结果不相等的是（　　）

A、 $\sqrt{(- 4) \times (- 9)}$ B、2×3 C、 $\sqrt{4} + \sqrt{9}$ D、 $(- \sqrt{6})^{2}$

查看试题解析
4. 下列二次根式中，与 $\sqrt{3}$ 属于同类二次根式的是（）

A、 $\sqrt{12}$ B、 $\sqrt{20}$ C、 $\sqrt{28}$ D、 $\sqrt{32}$

查看试题解析
5. 已知 $a ､ b ､ c$ 分别为三角形的三条边，下列条件中，不能判断 $△ A B C$ 为直角三角形的是（）

A、 $a^{2} + b^{2} = c^{2}$ B、 $∠ A + ∠ B = ∠ C$ C、 $a : b : c = 1 : 2 : 3$ D、 $a = 3, b = 4, c = 5$

查看试题解析
6. 下列说法正确的是（）

A、菱形的四个内角都是直角 B、正方形的每一条对角线平分一组对角 C、矩形的对角线互相垂直 D、平行四边形是轴对称图形

查看试题解析
7. 下列各图是以直角三角形各边为边，在三角形外部画正方形得到的，每个正方形中的数及字母 $S$ 表示所在正方形的面积．其中 $S$ 的值恰好等于10的是（）

A、 B、 C、 D、

查看试题解析
8. 如图，在矩形 $A B C D$ 中，对角线 $A C, B D$ 交于点 $O$ ，若 $∠ A O B = 6 0^{∘}$ ， $A B = 2$ ，则对角线 $A C$ 的长是（）

A、1 B、2 C、3 D、4

查看试题解析
9. 如图，在平面直角坐标系 $x O y$ 中，四边形 $A B C D$ 是菱形， $∠ A B C = 12 0^{∘}$ ，点 $B$ 的坐标为 $(0, - 3)$ ，则点 $A$ 的坐标为（）

A、 $(- 3 \sqrt{3}, 0)$ B、 $(3 \sqrt{3}, 0)$ C、 $(- 6, 0)$ D、 $(6, 0)$

查看试题解析
10. 如图，数学老师用四根长度相等的木条首尾顺次相接制成一个图1所示的菱形教具，此时测得 $∠ D = 6 0^{∘}$ ，对角线 $A C$ 长为 $16 c m$ ，改变教具的形状成为图2所示的正方形，则正方形的边长为（）

A、 $8 c m$ B、 $4 \sqrt{2} c m$ C、 $16 c m$ D、 $16 \sqrt{2} c m$

查看试题解析
11. 某数学兴趣小组开展了笔记本电脑的张角大小的实践探究活动．如图，当张角为 $∠ B A F$ 时，顶部边缘 $B$ 处距离桌面的高度 $B C$ 为 $7 c m$ ，此时底部边缘 $A$ 处与 $C$ 处间的距离 $A C$ 为 $24 c m$ ，小组成员调整张角的大小继续探究，最后发现当张角为 $∠ D A F$ 时（ $D$ 是 $B$ 的对应点），顶部边缘 $D$ 处到桌面的距离 $D E$ 为 $20 c m$ ，则底部边缘 $A$ 处与 $E$ 之间的距离 $A E$ 为（）

A、 $15 c m$ B、 $18 c m$ C、 $21 c m$ D、 $24 c m$

查看试题解析
12. 我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”，后人称之为“赵爽弦图”，它是由4个全等的直角三角形和一个小正方形组成一个大正方形．如图，直角三角形的直角边长为 $a ､ b$ ，斜边长为 $c$ ．若 $b - a = 2, c = 10$ ，则 $a + b$ 的值为（）

A、12 B、14 C、16 D、18

查看试题解析

二、填空题（本大题共6题，每小题2分，共12分．）

13. 式子 $y = \frac{1}{\sqrt{x - 5}}$ 在实数范围内有意义，则实数x的取值范围是.

查看试题解析
14. 一直角三角形两条直角边长分别为3和4，则该三角形的斜边长为．

查看试题解析
15. 当 $a < - 1$ 时， $\sqrt{(a + 1)^{2}} =$ ．

查看试题解析
16. 如图，一技术人员用刻度尺（单位： $c m$ ）测量某三角形部件的尺寸．已知 $∠ A C B = 9 0^{∘}$ ，点 $D$ 为边 $A B$ 的中点，点 $A ､ B$ 对应的刻度为1，7，则 $C D =$ $c m$ ．

查看试题解析
17. 如图，在周长为600米的三角形地块中修建如图所示的三条水渠，则水渠的总长为．米．

查看试题解析
18. 如图，某自动感应门的正上方A处装着一个感应器，离地 $A B = 2.5$ 米，当人体进入感应器的感应范围内时，感应门就会自动打开.一个身高1.6米的学生 $C D$ 正对门，缓慢走到离门1.2米的地方时（ $B C = 1.2$ 米），感应门自动打开，则 $A D =$ 米.

查看试题解析

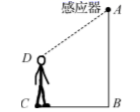
三、解答题（本大题共8小题，共72分，解答题应写出文字说明，证明过程或演算步骤．）

19. 计算 $4 \times \frac{\sqrt{3}}{2} + (2024)^{0} - {(\frac{1}{2})}^{- 1} - | 2 \sqrt{3} |$ ．

查看试题解析
20. 解不等式组 ${\begin{array}{l} x - 2 > \frac{x - 2}{3} \\ \frac{x - 1}{2} \leq 4 - x \end{array}$ ，并在数轴上表示此不等式组的解集．

查看试题解析
21. 阅读材料：如果一个三角形的三边长分别为 $a, b, c$ ，记 $p = \frac{a + b + c}{2}$ ，那么这个三角形的面积为 $S = \sqrt{p (p - a) (p - b) (p - c)}$ ．这个公式叫“海伦公式”，它是利用三角形的三条边的边长直接求三角形面积的公式，中国秦九韶也得出了类似的公式，称三斜求积术，故这个公式又被称为“海伦—秦九韶公式”．完成下列问题：
如图，在 $△ A B C$ 中， $a = 8, b = 5, c = 7$ ．

(1)、求 $△ A B C$ 的面积；

(2)、过点 $A$ 作 $A D ⊥ B C$ ，垂足为 $D$ ，求线段 $A D$ 的长．

查看试题解析
22. 【阅读理解】爱思考的小名在解决问题：已知 $a = \frac{1}{2 + \sqrt{3}}$ ，求 $2 a^{2} - 8 a + 1$ 的值．他是这样分析与解答的：
$∵ a = \frac{1}{2 + \sqrt{3}} = \frac{2 - \sqrt{3}}{(2 + \sqrt{3}) (2 - \sqrt{3})} = 2 - \sqrt{3}, a - 2 = - \sqrt{3}$ ．
$∴ (a - 2)^{2} = 3$ ，即 $a^{2} - 4 a + 4 = 3$ ．
$∴ a^{2} - 4 a = - 1$ ．
$∴ 2 a^{2} - 8 a + 1 = 2 (a^{2} - 4 a) + 1 = 2 \times (- 1) + 1 = - 1$ ．
请你根据小名的分析过程，解决如下问题：

(1)、计算： $\frac{1}{\sqrt{2} + 1} =$ ；

(2)、计算： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{100} + \sqrt{99}} =$ ；

(3)、若 $a = \frac{1}{\sqrt{5} - 2}$ ，求 $3 a^{2} - 12 a - 1$ 的值．

查看试题解析
23. 如图，四边形 $A B C D$ 中，对角线 $A C ､ B D$ 相交于点 $O, A O = C O$ ， $B O = D O$ ，且 $∠ A B C + ∠ A D C = 18 0^{∘}$ ．

(1)、求证：四边形 $A B C D$ 是矩形．

(2)、 $D E ⊥ A C$ 垂足为点 $E$ ，交 $B C$ 于点 $F$ ，若 $∠ A D F : ∠ F D C = 2 : 1$ ，则 $∠ B D F$ 的度数是多少？

查看试题解析
24. 某巨型摩天轮的最低点距离地面 $10 m$ ，圆盘半径为 $50 m$ ．摩天轮的圆周上均匀地安装了若干个座舱（本题中将座舱视为圆周上的点），游客在距离地面最近的位置进舱．小明、小丽先后从摩天轮的底部入舱出发开始观光，当小明观光到达点 $P$ 时，小丽到达点 $Q$ ，此时 $∠ P O Q = 9 0^{∘}$ ，且小丽距离地面 $20 m$ ．

(1)、求证： $△ O C P ≅ △ Q D O$ ；

(2)、求此时两人所在座舱距离地面的高度差．

查看试题解析
25. 如图，在 $R t △ A B C$ 中， $∠ C = 9 0^{∘}$ ，延长 $C B$ 至 $D$ ，使得 $B D = C B$ ，过点 $A, D$ 分别作 $A E$ $∥$ $B D, D E$ $∥$ $B A, A E$ 与 $D E$ 相交于点 $E$ ．下面是两位同学的对话：
小星：由题目的已知条件，若连接 $B E$ ，则可证明 $B E ⊥ C D$ ．
小红：由题目的已知条件，若连接 $C E$ ，则可证明 $C E = D E$ ．

(1)、请你选择一位同学的说法，并进行证明；

(2)、连接 $A D$ ，若 $A D = 5 \sqrt{2}, \frac{C B}{A C} = \frac{2}{3}$ ，求 $A C$ 的长．

查看试题解析
26. 台风“烟花”风力强，累计降雨量大，影响范围大，有极强的破坏力．如图，台风“烟花”中心沿东西方向 $A B$ 由 $A$ 向 $B$ 移动，已知点 $C$ 为一海港，且点 $C$ 与直线 $A B$ 上的两点 $A ､ B$ 的距离分别为 $A C = 300 k m, B C = 400 k m$ ，又 $A B = 500 k m$ ，经测量，距离台风中心 $260 k m$ 及以内的地区会受到影响．

(1)、海港 $C$ 受台风影响吗？为什么？

(2)、若台风中心的移动速度为25千米/时，则台风影响该海港持续的时间有多长？

查看试题解析