广东省东莞市常平镇2023-2024年七年级下学期数学期中试题

试卷更新日期：2024-05-27 类型：期中考试

进入出卷网下载

一、单项选择题（本大题共10小题，每小题3分，共30分）

1. 64的平方根是（）

A、 $- 8$ B、8 C、 $\pm 8$ D、 $\pm 4$

查看试题解析
2. 下列各式中，是关于 $x$ ， $y$ 的二元一次方程的是（）

A、 $2 x - y$ B、 $x y + x - 2 = 0$ C、 $x - 3 y = - 1$ D、 $\frac{2}{x} - y = 0$

查看试题解析
3. 在平面直角坐标系中，将点 $(- 2, 3)$ 向右平移4个单位长度后得到的点的坐标为（）

A、 $(- 6, 3)$ B、 $(2, 3)$ C、 $(- 2, 7)$ D、 $(- 2, - 1)$

查看试题解析
4. 下列哪对x ， y的值是二元一次方程 $x + 2 y = 6$ 的解（）

A、 ${\begin{cases} x = 2 \\ y = 2 \end{cases}$ B、 ${\begin{cases} x = 0 \\ y = 2 \end{cases}$ C、 ${\begin{cases} x = - 2 \\ y = - 2 \end{cases}$ D、 ${\begin{cases} x = 3 \\ y = 1 \end{cases}$

查看试题解析
5. 下列运算正确的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $- \sqrt{3^{2}} = 3$ C、 $\sqrt[3]{- 9} = - 3$ D、 $\pm \sqrt{9} = \pm 3$

查看试题解析
6. 如图，点E在AD延长线上，下列条件能判断 $A B ∥ C D$ 的是（）

A、 $∠ 3 = ∠ 4$ B、 $∠ C + ∠ A D C = 180 °$ C、 $∠ C = ∠ C D E$ D、 $∠ 1 = ∠ 2$

查看试题解析
7. 如图，直线MN与CD相交于点O ， $∠ M O C = 80 °$ ， $∠ 1 = 35 °$ ，则∠2的度数是（）

A、35 B、40° C、45° D、55°

查看试题解析
8. 已知点 $P (m + 2, 2 m - 4)$ 在x轴上，则点P的坐标是（）

A、 $(0, 4)$ B、 $(4, 0)$ C、 $(- 4, 0)$ D、 $(0, - 4)$

查看试题解析
9. 下列说法中正确的个数是（）
①无限小数都是无理数；②带根号的数都是无理数；③数轴上的点表示的数都是实数；
④有理数都是有限小数；⑤实数分为正实数，0，负实数．

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 如图，科技兴趣小组爱好编程的同学编了个电子跳蛙程序，跳蛙P在平面直角坐标系中按图中箭头所示方向跳动，第1次从原点跳到点 $(1, 1)$ ，第2次接着跳到点 $(2, 0)$ ，第3次接着跳到点 $(3, 2)$ ， …按这样的跳动规律，经过第2024次跳动后，跳蛙P的坐标是（）

A、 $(2024, 0)$ B、 $(2024, 1)$ C、 $(2023, 1)$ D、 $(2024, 2)$

查看试题解析

二、填空题

11. 比较大小： $\sqrt{5}$ 3．（“＞”“＜”或“=”）

查看试题解析
12. 将命题“同角的余角相等”改成“如果…那…的形式为：．

查看试题解析
13. 在平面直角坐标系的第四象限内有一点P ，点P到x轴的距离为7．到y轴的距离为8，则点P的坐标为．

查看试题解析
14. 已知 ${\begin{cases} x = - 1 \\ y = 2 \end{cases}$ 是方程 $a x + y = 4$ 的一个解，则a的值为．

查看试题解析
15. 如图，将一张长方形纸片沿EF折叠后，点D ， C分别落在 $D^{'}$ ， $C^{'}$ 的位置，ED的延长线与BC交于点G ．若 $∠ E F G = 55 °$ ，则 $∠ 1 =$ ．

查看试题解析

三、解答题

16. 计算： $\sqrt{2} (\sqrt{2} - 1) + \sqrt[3]{- 27} + | \sqrt{2} - 3 |$ ．

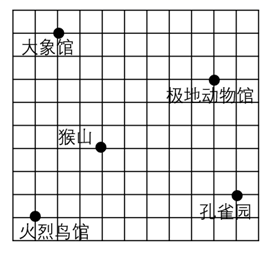
查看试题解析
17. 如图，图中每个小正方形的边长均为1，已知极地动物馆的坐标为 $(5 ， 4)$ ，孔雀园的坐标为 $(6 ， - 1)$ ，先建立平面直角坐标系，再表示其他三个景点的坐标．

查看试题解析

四、解答题

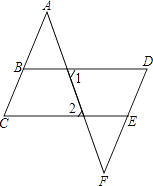
18. 解方程组： ${\begin{cases} 4 x - 3 y = 6 \\ 3 x - y = 7 \end{cases}$

查看试题解析
19. 如图，已知∠1=∠2，∠C=∠D，求证：∠A=∠F．

查看试题解析
20. 如图，直角坐标系中，△ABC的顶点都在网格点上，其中C点坐标为 $(1, 2)$ ，将△ABC先向左平移2个单位长度，再向上平移1个单位长度，得到 $△ A^{'} B^{'} C^{'}$ ．

(1)、画出 $△ A^{'} B^{'} C^{'}$ ；

(2)、求△ABC的面积．

查看试题解析

五、解答题

21. 某校为丰富学生的校园生活，准备从某体育用品商店次性购买若干个足球和篮球，若购买3个足球和2个篮球共需210元，购买2个足球和1个篮球共需130元，请问购买一个足球，一个篮球各需多少元？

查看试题解析
22. 如图所示， $E F ⊥ B C$ 于点F ， $D M ⊥ B C$ 于点M ， $∠ 1 = ∠ 2$ ， $∠ 3 = ∠ C$ ．求证： $A B ∥ M N$ ．

查看试题解析
23. 小明制作了一张面积为81cm²的正方形贺卡想寄给朋友．现有一个长方形信封如图所示，长、宽之比为5：3，面积为150cm² ．

(1)、求长方形信封的长和宽：

(2)、小明能将贺卡不折叠就放入此信封吗？请通过计算给出判断，

查看试题解析

六、解答题（共2小题，每小题10分，共20分）

24. 如图，直线AB相与CD相交于O ， OF ， OD分别是 $∠ A O E$ ， $∠ B O E$ 平分线．

(1)、写出∠DOE的两个补角：

(2)、若 $∠ D O E = 30 °$ ．求∠BOC和∠EOF的度数；

(3)、试问射线OD与OF之间有什么特殊的位置关系？为什么？

查看试题解析
25. 如图，在长方形OABC中，O为平面直角坐标系的原点，点A的坐标为 $(a, 0)$ ．点C的坐标为 $(0, b)$ 且a、b满足 $\sqrt{a - 8} + | b - 12 | = 0$ ，点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着 $O - C - B - A - O$ 的线路移动．

(1)、点B的坐标为；当点P移动5秒时，点P的坐标为；

(2)、在移动过程中，当点P到x轴的距离为4个单位长度时，求点P移动的时间；

(3)、在 $O - C - B$ 的线路移动过程中，是否存在点P使△OBP的面积是20，若存在，请算出点P移动的时间；若不存在，请说明理由．

查看试题解析