2024年广东省深圳市中考数学仿真模拟试卷(二)
试卷更新日期:2024-05-27 类型:中考模拟
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,只有一个是正确的)
-
1. 下列四个数中,是无理数的是( )A、3.14 B、 C、 D、02. 一粒大米的质量约为0.000021千克,将0.000021这个数用科学记数法表示正确的是( )A、 B、 C、 D、3. 下列图形中,轴对称图形的个数为( )
 A、4 B、3 C、2 D、14. 小莉的作业本上有以下四题,正确的是( )A、 B、 C、 D、5. 如图,直线 , 直线分别交 , 于点 , , 以点B为圆心,长为半径画弧,若在弧上存在点C使 , 则的度数是( )
A、4 B、3 C、2 D、14. 小莉的作业本上有以下四题,正确的是( )A、 B、 C、 D、5. 如图,直线 , 直线分别交 , 于点 , , 以点B为圆心,长为半径画弧,若在弧上存在点C使 , 则的度数是( )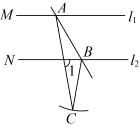 A、 B、 C、 D、6. 某种柑橘果肉清香、酸甜适度,深受人们的喜爱,也是馈赠亲友的上佳礼品.首批柑橘成熟后,某电商用3500元购进这种柑橘进行销售,面市后,线上订单猛增,供不应求,该电商又用2500元购进第二批这种柑橘,由于更多柑橘成熟,单价比第一批每箱便宜了4元,但数量与第一批的数量一样多,求购进的第一批柑橘的单价.设购进的第一批柑橘的单价为x元,根据题意可列方程为( )A、 B、 C、 D、7. 如图所示,一次函数与正比例函数的图象相交于点 , 下列判断错误的是( )
A、 B、 C、 D、6. 某种柑橘果肉清香、酸甜适度,深受人们的喜爱,也是馈赠亲友的上佳礼品.首批柑橘成熟后,某电商用3500元购进这种柑橘进行销售,面市后,线上订单猛增,供不应求,该电商又用2500元购进第二批这种柑橘,由于更多柑橘成熟,单价比第一批每箱便宜了4元,但数量与第一批的数量一样多,求购进的第一批柑橘的单价.设购进的第一批柑橘的单价为x元,根据题意可列方程为( )A、 B、 C、 D、7. 如图所示,一次函数与正比例函数的图象相交于点 , 下列判断错误的是( ) A、关于x的方程的解是 B、关于x的不等式的解集是 C、当时,函数的值比函数的值大 D、关于x , y的方程组的解是8. 如图,EF是△ABC的中位线,点O是EF上一点,且满足 , 则△ABC 的面积与△AOC的面积之比为( )
A、关于x的方程的解是 B、关于x的不等式的解集是 C、当时,函数的值比函数的值大 D、关于x , y的方程组的解是8. 如图,EF是△ABC的中位线,点O是EF上一点,且满足 , 则△ABC 的面积与△AOC的面积之比为( ) A、 B、 C、 D、9.
A、 B、 C、 D、9.如图,A,B,C,D为⊙O的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O路线作匀速运动,设运动时间为t(秒).∠APB=y(度),则下列图象中表示y与t之间函数关系最恰当的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 10. 如图,△ABC的顶点都在正方形网格的格点上,则tanA的值是( )
10. 如图,△ABC的顶点都在正方形网格的格点上,则tanA的值是( )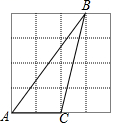 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题(本题有5小题,每小题3分,共15分)
-
11. 的公因式是 .12. 方程x2﹣6x+4=0的两个实根分别为x1 , x2 , 那么x1x2﹣x1﹣x2的值为 .13. 已知数据 的平均数是2,方差是3,则一组新数据 的平均数是 , 方差是 .14. 如图,双曲线y= 经过Rt△BOC斜边上的点A,且满足 = ,与BC交于点D,S△BOD=21,求k= .
 15. 如题图所示,在中存在一面积为的内切圆,其圆心为点 , 连接 , 若满足 , , , 则实数的值为 .
15. 如题图所示,在中存在一面积为的内切圆,其圆心为点 , 连接 , 若满足 , , , 则实数的值为 .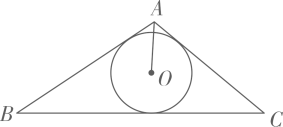
三、解答题(共7题,共55分)
-
16. 计算: .17. 先化简,再求值: , 其中 .18. 新颁布的《义务教育课程方案和课程标准(2022年版)》优化了课程设置,将劳动从综合实践活动课程中独立出来,彰显劳动教育的重要性.为了解某校学生一周内劳动教育情况,随机抽查部分学生一周内课外劳动时间,将数据进行整理并制成如下统计图的图1和图2.

请根据图中提供的信息,解答下面的问题:
(1)、求图1中m的值为 , 此次抽查数据的中位数是 h;(2)、求该校此次抽查的学生一周内平均课外劳动时间;(3)、若该校共有2000名学生,请你估计该校学生一周内课外劳动时间不小于的人数.19. 图、图、图均是的正方形网格,每个小正方形的边长均为 , 每个小正方形的顶点称为格点点、均在格点上,只用无刻度的尺,分别在给定的网格中按下列要求作 , 点在格点上.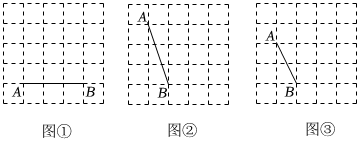 (1)、在图中,的面积为;(2)、在图中,的面积为;(3)、在图中,是面积为的钝角三角形.20. 超市购进A、B两种商品,购进4件A种商品比购进5件B种商品少用10元,购进20件A种商品和10件B种商品共用去160元.(1)、求A、B两种商品每件进价分别是多少元?(2)、若该商店购进A、B两种商品共200件,都标价10元出售,售出一部分商品后降价促销,以标价的八折售完所有剩余商品,以10元售出的商品件数比购进A种商品的件数少30件,该商店此次销售A、B两种商品共获利不少于640元,求至少购进A种商品多少件?21. 某校项目式学习小组开展项目活动,过程如下:
(1)、在图中,的面积为;(2)、在图中,的面积为;(3)、在图中,是面积为的钝角三角形.20. 超市购进A、B两种商品,购进4件A种商品比购进5件B种商品少用10元,购进20件A种商品和10件B种商品共用去160元.(1)、求A、B两种商品每件进价分别是多少元?(2)、若该商店购进A、B两种商品共200件,都标价10元出售,售出一部分商品后降价促销,以标价的八折售完所有剩余商品,以10元售出的商品件数比购进A种商品的件数少30件,该商店此次销售A、B两种商品共获利不少于640元,求至少购进A种商品多少件?21. 某校项目式学习小组开展项目活动,过程如下:项目主题:测量旗杆高度

问题驱动:能利用哪些科学原理来测量旗杆的高度?
组内探究:由于旗杆较高,需要借助一些工具来测量,比如自制的直角三角形硬纸板,标杆,镜子,甚至还可以利用无人机…确定方法后,先画出测量示意图,然后实地进行测量,并得到具体数据,从而计算旗杆的高度.
成果展示:下面是同学们进行交流展示时的部分测量方案:
方案一
方案二
…
测量工具
标杆,皮尺
自制直角三角板硬纸板,皮尺
…
测量示意图

说明:线段AB表示学校旗杆,小明的眼睛到地面的距离CD=1.7m,测点F与B,D在同一水平直线上,D,F,B之间的距离都可以直接测得,且A,B,C,D,E,F都在同一竖直平面内,点A,C,E三点在同一直线上.

说明:线段AB表示旗杆,小明的身高CD=1.7m,测点D与B在同一水平直线上,D,B之间的距离可以直接测得,且A,B,C,D,E,F,G都在同一竖直平面内,点A,C,E三点在同一直线上,点C,F,G三点在同一直线上.
测量数据
B,D之间的距离
16.8m
B,D之间的距离
16.8m
…
D,F之间的距离
1.35m
EF的长度
0.50m
…
EF的长度
2.60m
CE的长度
0.75m
…
…
…
根据上述方案及数据,请你选择一个方案,求出学校旗杆AB的高度.(结果精确到0.1m);
22. “转化”是解决数学问题的重要思想方法,通过构造图形全等或者相似建立数量关系是处理问题的重要手段. (1)、【问题情景】:如图(1),正方形中,点是线段上一点(不与点、重合),连接.将绕点顺时针旋转90°得到 , 连接 , 求的度数.
(1)、【问题情景】:如图(1),正方形中,点是线段上一点(不与点、重合),连接.将绕点顺时针旋转90°得到 , 连接 , 求的度数.以下是两名同学通过不同的方法构造全等三角形来解决问题的思路,
①小聪:过点作的延长线的垂线;
②小明:在上截取 , 使得;
请你选择其中一名同学的解题思路,写出完整的解答过程.
(2)、【类比探究】:如图(2)点是菱形边上一点(不与点、重合), , 将绕点顺时针旋转得到 , 使得(),则的度数为(用含的代数式表示)(3)、【学以致用】:如图(3),在(2)的条件下,连结 , 与相交于点 , 当时,若 , 求的值.