2024年广东省深圳市八年级下册数学期末模拟试卷(三)

试卷更新日期：2024-05-24 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分，每小题有四个选项，只有一个是正确的）

1. “二十四节气”是中华上古农耕文明的智慧结晶．下列四幅标识图，其中文字上面图案是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 若m＜n，则下列不等式正确的是（）

A、 $m - 1 < n - 1$ B、 $\frac{m}{2} ＞ \frac{n}{2}$ C、 $4 m > 4 n$ D、 $m^{2} > n^{2}$

查看试题解析
3. 下列式子： $- 5 x$ ， $\frac{1}{a + b}$ ， $\frac{1}{2} a^{2} - \frac{1}{2} b^{2}$ ， $\frac{3}{10 m}$ ， $\frac{2}{π}$ ，其中分式有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
4. 若 $x$ 、 $y$ 的值均扩大为原来的 $5$ 倍，则下列分式的值保持不变的是（）

A、 $\frac{x + y}{x y}$ B、 $\frac{x + y}{x - y}$ C、 $\frac{x + y}{y + 1}$ D、 $\frac{x}{y + 1}$

查看试题解析
5. 如图所示，一次函数 $y = k x + b (k \neq 0)$ 与正比例函数 $y = m x (m \neq 0)$ 的图象相交于点 $M (1, 2)$ ，下列判断错误的是（）

A、关于x的方程 $m x = k x + b$ 的解是 $x = 1$ B、关于x的不等式 $m x \geq k x + b$ 的解集是 $x > 1$ C、当 $x < 0$ 时，函数 $y = k x + b$ 的值比函数 $y = m x$ 的值大 D、关于x ， y的方程组 ${\begin{array}{l} y - m x = 0 \\ y - k x = b \end{array}$ 的解是 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$

查看试题解析
6. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ，斜边 $A B$ 的垂直平分线 $l$ 交 $A C$ 于点 $D$ ，连接 $B D .$ 若 $A B = 13$ ， $B C = 5$ ，则 $△ B C D$ 的周长为( )

A、 $18$ B、 $17$ C、 $11.5$ D、 $11$

查看试题解析
7. 如图， $A B ⊥ A F$ ， $E F ⊥ A F$ ， $B E$ 与 $A F$ 交于点 $C$ ，点 $D$ 是 $B C$ 的中点， $∠ A E B = 2 ∠ B$ ．若 $B C = 8$ ， $E F = \sqrt{7}$ ，则 $A F$ 的长是（）

A、 $\sqrt{6}$ B、 $\sqrt{7}$ C、3 D、5

查看试题解析
8. 如图，平行四边形ABCD的对角线AC与BD相交于点O ， AE⊥BC于E ， AB＝ $\sqrt{3}$ ，AC＝2，BD＝4，则AE的长为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{3}{2}$ C、 $\frac{\sqrt{21}}{7}$ D、 $\frac{2 \sqrt{21}}{7}$

查看试题解析
9. 已知a，b，c分别是△ABC的三边长，若 $a^{2} + 2 a b + b^{2} = c^{2} + 24$ ， $a + b - c = 4$ ，则△ABC的周长是（）

A、3 B、6 C、8 D、12

查看试题解析
10. 如图，在 $△ A B D$ 中， $A D = A B$ ， $∠ D A B = 90 °$ ，在 $△ A C E$ 中， $A C = A E$ ， $∠ E A C = 90 °$ ， $C D$ ， $B E$ 相交于点 $F$ ，有下列四个结论： $① ∠ B D C = ∠ B E C$ ； $② F A$ 平分 $∠ D F E$ ； $③ D C ⊥ B E$ ； $④ D C = B E .$ 其中，正确的结论有( )

A、 $① ② ③ ④$ B、 $① ③ ④$ C、 $② ③$ D、 $② ③ ④$

查看试题解析

二、填空题（本题有5小题，每小题3分，共15分）

11. 分解因式： $a^{2} b - a^{2} =$ ．

查看试题解析
12. 关于 $x$ 的分式方程 $\frac{m}{x - 1} + \frac{3}{1 - x} = 1$ 的解为负数，则 $m$ 的取值范围是．

查看试题解析
13. 不等式组 ${\begin{array}{l} 2 (x + 1) < 3 x - 6 \\ x < 4 m \end{array}$ 无解，则m的取值范围是．

查看试题解析
14. “绿水青山就是金山银山”.某地为美化环境，计划种植树木1000棵.由于志愿者的加入，实际每天植树的棵数比原计划增加了25%，结果提前2天完成任务.则实际每天植树棵.

查看试题解析
15. 在 $▱ A B C D$ 中， $A B = 6 c m$ ， $A D = 10 c m$ ，点P在 $A D$ 边上以每秒 $1 c m$ 的速度从点A向点D运动．点Q在 $B C$ 边上以每秒 $4 c m$ 的速度从点C出发，在 $C B$ 之间往返运动．两个点同时出发，当点P到达点D时停止（同时点Q也停止运动），设运动时间为t秒．当 $5 < t < 10$ 时，运动时间 $t =$ 时，以P、D、Q、B为顶点的四边形是平行四边形．

查看试题解析

三、解答题（共7题，共55分）

16. 解不等式（组） ${\begin{matrix} 2 x - 2 > x ① \\ \frac{5}{3} x + 1 \geq 2 x ② \end{matrix}$ ，并把它的解集表示在数轴上．

查看试题解析
17. 先化简，再求值： $(\frac{x}{x - 1} - 1) \div \frac{x^{2} - x}{x^{2} - 2 x + 1}$ ，再从不等式 $- 1 \leq x \leq 1$ 的整数解中选择一个适当的数代入求值．

查看试题解析
18. 如图，在平面直角坐标系中，△ABC三个顶点的坐标分别为A（-2，4），B（-4，1），C（0，1）．

⑴画出与△ABC关于x轴对称的△A₁B₁C₁ ，并写出点C₁的坐标；

⑵画出以C₁为旋转中心，将△A₁B₁C₁逆时针旋转90°后的△A₂B₂C₂；

⑶尺规作图：连接A₁A₂ ，在C₁A₂边上求作一点P，使得点P到A₁A₂的距离等于PC₁的长（保留作图痕迹，不写作法）；

⑷请直接写出∠C₁A₁P的度数为．

查看试题解析
19. 如图，∠B=∠C=90°，点E为BC的中点，DE平分∠ADC，过点E作EF⊥AD，垂足为F，连结AE、BF．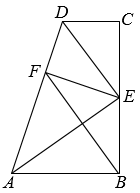

(1)、求证：AE是∠DAB的平分线．

(2)、求证：线段AE垂直平分BF．

查看试题解析
20. 某果园实验基地推广甲、乙两种芒果苗，已知乙种芒果苗比甲种芒果苗每株贵 $2$ 元，且用 $240$ 元钱购买甲种芒果苗的株数与用 $360$ 元钱购买乙种芒果苗的株数刚好相同．

(1)、求甲、乙两种芒果苗每株的价格；

(2)、果农 $A$ 准备从甲、乙两种芒果苗中选购一种，已知购买数量相同且数量不少于 $500$ 株，该果园实验基地负责人可给予以下优惠：购买甲种芒果苗每株按原售价九折优惠；购买乙种芒果苗，不多于 $500$ 株按原售价付款不优惠，超过 $500$ 株每株按原售价五折优惠 $.$ 请帮助果农 $A$ 判断购买哪种芒果苗更省钱．

(3)、果农 $B$ 计划购买甲、乙两种芒果苗共 $300$ 株 $.$ 调查统计发现，甲、乙两种芒果苗的成活率分别为 $90 %$ 、 $95 %$ ，要使这批芒果苗的成活率不低于 $93 %$ ，且使购买芒果苗的费用最低，应如何选购芒果苗？最低费用是多少？

查看试题解析
21. 阅读下面的材料：把一个分式写成两个分式的和叫作把这个分式表示成“部分分式”.
例：将分式 $\frac{1 - 3 x}{x^{2} - 1}$ 表示成部分分式，解：设 $\frac{1 - 3 x}{x^{2} - 1} = \frac{M}{x + 1} + \frac{N}{x - 1}$ ，将等式右边通分，得 $\frac{M (x - 1) + N (x + 1)}{(x + 1) (x - 1)} = \frac{(M + N) x + (N - M)}{x^{2} - 1}$ ，依据题意，得 ${\begin{array}{l} M + N = 3 \\ N - M = 1 \end{array}$ ，解得 ${\begin{array}{l} M = - 2 \\ N = - 1 \end{array}$ ，所以 $\frac{1 - 3 x}{x^{2} - 1} = \frac{- 2}{x + 1} + \frac{- 1}{x - 1}$ 请你适用上面所学到的方法，解决下面的问题：

(1)、 $\frac{1}{n (n + 1)} = \frac{A}{n} + \frac{B}{n + 1}$ （A ， B为常数），则 $A =$ ， $B =$ ；

(2)、一个容器装有 $1 L$ 水，按照如下要求把水倒出：第1次倒出 $\frac{1}{2} L$ 水，第2次倒出的水量是 $\frac{1}{2} L$ 的 $\frac{1}{3}$ ，第3次倒出的水量是 $\frac{1}{3} L$ 的 $\frac{1}{4}$ ，第4次倒出的水量是 $\frac{1}{4} L$ 的 $\frac{1}{5}$ …第n次倒出的水量是 $\frac{1}{n} L$ 的 $\frac{1}{n + 1}$ …按照这种倒水的方法，这 $1 L$ 的水是否能倒完？如果能，多少次能倒完？如果不能，请说明理由；

(3)、按照（2）的条件，现在开始重新实验，按照如下要求把水倒出：第1次倒出 $\frac{1}{3} L$ 水，第2次倒出的水量是 $\frac{1}{15} L$ ，第3次倒出的水量是 $\frac{1}{35} L$ ，第4次倒出的水量是 $\frac{1}{63} L$ ，请问经过多少次操作后，杯内剩余水量能否变成原来水量的 $\frac{100}{199}$ ？试说明理由.

查看试题解析
22.

(1)、【问题探究】如图，已知 $A D$ 是 $△ A B C$ 的中线，延长 $A D$ 至点E，使 $D E = A D$ ，连接 $B E$ ， $C E$ 可得四边形 $A B E C$ ，求证：四边形 $A B E C$ 是平行四边形．
请你完善以下证明过程：
∵ $A D$ 是 $△ A B C$ 的中线
∴=
∵ $D E = A D$
∴四边形 $A B E C$ 是平行四边形

(2)、【拓展提升】如图2，在 $△ A B C$ 的中线 $A D$ 上任取一点M（不与点A重合），过点M、点C分别作 $M E / / A B$ ， $C E / / A D$ ，连接 $A E$ ．
求证：四边形 $A B M E$ 是平行四边形．

(3)、【灵活应用】如图，在 $△ A B C$ 中， $∠ B = 90 °$ ， $A B = 4$ ， $B C = 6$ ，点D是 $B C$ 的中点，点M是直线 $A D$ 上的动点，且 $M E / / A B$ ， $C E / / A D$ ，当 $M E + M C$ 取最小值时，求线段 $C E$ 的长．

查看试题解析