2024年广东省深圳市八年级下册数学期末模拟试卷(一)
试卷更新日期:2024-05-24 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,只有一个是正确的)
-
1. 下列与杭州亚运会有关的图案中,中心对称图形是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列各项变形,是因式分解的是( )A、a(a﹣2)=a2﹣2a B、a2+4a﹣5=(a+5)(a﹣1) C、y2﹣1=y(y﹣ ) D、am+bm+c=m(a+b)+c3. 如果 , 那么下列各式中正确的是( )A、 B、 C、 D、4. 已知等腰三角形的一边长为2,一边的长为6,则此等腰三角形的周长为( )A、14 B、12 C、10 D、10或145. 下列分式是最简分式的是( )A、 B、 C、 D、6. 下列在数轴上表示的不等式组的解集,正确的是( )A、
2. 下列各项变形,是因式分解的是( )A、a(a﹣2)=a2﹣2a B、a2+4a﹣5=(a+5)(a﹣1) C、y2﹣1=y(y﹣ ) D、am+bm+c=m(a+b)+c3. 如果 , 那么下列各式中正确的是( )A、 B、 C、 D、4. 已知等腰三角形的一边长为2,一边的长为6,则此等腰三角形的周长为( )A、14 B、12 C、10 D、10或145. 下列分式是最简分式的是( )A、 B、 C、 D、6. 下列在数轴上表示的不等式组的解集,正确的是( )A、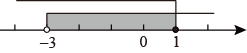 B、
B、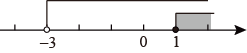 C、
C、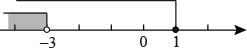 D、
D、 7. 关于x的不等式组有且只有2个整数解,则符合要求的所有整数a的和为( )A、 B、 C、0 D、78. 若分式方程无解,则的值是( )A、或 B、 C、或 D、或9. 几个同学包租一辆面包车去旅游,面包车的租价为180元,后来又增加了两名同学,租车价不变,结果每个同学比原来少分摊了3元车费.若设原计划参加旅游的同学共有人,则根据题可列方程( )A、 B、 C、 D、10. 如图,在等边△PQB中,点A为PQ上一动点(不与P,Q重合),再以AB为边作等边△ABC,连接PC.有以下结论:①PB平分∠ABC;②AQ=CP;③PC//QB;④PB=PA+PC;⑤当 BC⊥BQ时,△ABC的周长最小,其中一定正确的有( )
7. 关于x的不等式组有且只有2个整数解,则符合要求的所有整数a的和为( )A、 B、 C、0 D、78. 若分式方程无解,则的值是( )A、或 B、 C、或 D、或9. 几个同学包租一辆面包车去旅游,面包车的租价为180元,后来又增加了两名同学,租车价不变,结果每个同学比原来少分摊了3元车费.若设原计划参加旅游的同学共有人,则根据题可列方程( )A、 B、 C、 D、10. 如图,在等边△PQB中,点A为PQ上一动点(不与P,Q重合),再以AB为边作等边△ABC,连接PC.有以下结论:①PB平分∠ABC;②AQ=CP;③PC//QB;④PB=PA+PC;⑤当 BC⊥BQ时,△ABC的周长最小,其中一定正确的有( )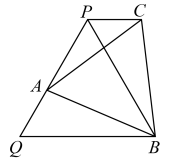 A、①②③ B、②③④ C、③④⑤ D、②③④⑤
A、①②③ B、②③④ C、③④⑤ D、②③④⑤二、填空题(本题有5小题,每小题3分,共15分)
-
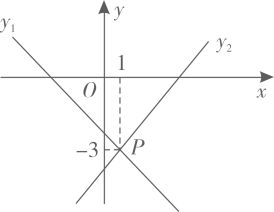
11. 分解因式: .12. 已知 , 则= .13. 如图,直线与相交于点 , 已知点的坐标为 , 则关于的不等式的解集是。
 14. 如图,矩形ABCD中,对角线AC、BD相交于点O , ∠AOB=60°,AE平分∠BAD交BC于点E , 连接OE , 则∠BOE的度数是 .
14. 如图,矩形ABCD中,对角线AC、BD相交于点O , ∠AOB=60°,AE平分∠BAD交BC于点E , 连接OE , 则∠BOE的度数是 . 15. 如图,在中, , 把绕边的中点O旋转后得 , 若直角顶点E恰好落在边上,且边交边于点G,则的面积为 .
15. 如图,在中, , 把绕边的中点O旋转后得 , 若直角顶点E恰好落在边上,且边交边于点G,则的面积为 .
三、解答题(共7题,共55分)
-
16. 解不等式组: , 并写出该不等式组的所有整数解.17. 化简求值: , 其中 .18. 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(5,4),B(1,1),C(5,1).

⑴请画出△ABC关于x轴对称的△A1B1C1 , 并写出点A1的坐标;
⑵以O为对称中心,画出△ABC关于O成中心对称的图形△A'B'C';
⑶请用无刻度的直尺画出∠ABC的平分线BQ(点Q在线段AC上)(保留作图辅助线).
19. 如图,在中, , 平分 , , 点在上,且 . 求证: .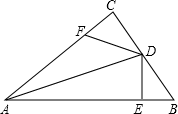 20. 学校需要购买一批篮球和足球,已知一个篮球比一个足球的单价高30元,买两个篮球和三个足球一共需要510元.(1)、求篮球和足球的单价分别为多少元?(2)、根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的 , 学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?(3)、若学校购买这批篮球和足球的总费用为(元 , 在(2)的条件下,求哪种方案能使总费用最小,并求出的最小值.21. 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.
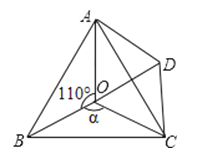
20. 学校需要购买一批篮球和足球,已知一个篮球比一个足球的单价高30元,买两个篮球和三个足球一共需要510元.(1)、求篮球和足球的单价分别为多少元?(2)、根据实际需要,学校决定购买篮球和足球共100个,其中篮球购买的数量不少于足球数量的 , 学校可用于购买这批篮球和足球的资金最多为10500元.请问有几种购买方案?(3)、若学校购买这批篮球和足球的总费用为(元 , 在(2)的条件下,求哪种方案能使总费用最小,并求出的最小值.21. 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=a.将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD.(1)求证:△COD是等边三角形;
(2)当a=150°时,试判断△AOD的形状,并说明理由;
(3)探究:当a为多少度时,△AOD是等腰三角形?
 22. 【问题背景】
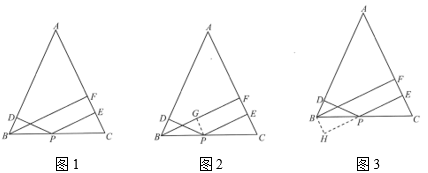
22. 【问题背景】某“数学学习兴趣小组”在学习了“等腰三角形的性质”和“平行四边形的性质和判定”后,在习题中发现了这样一个问题:如图1,在等腰中, , 点D、E分别是边上的点,点P是底边上的点,且 , 过点B作于点F,请写出线段、、之间满足的数量关系式.
同学们经过交流讨论,得到了如下两种解决思路:
解决思路1:如图2,过点P作于点G;
解决思路2:如图3,过点B作 , 交的延长线于点H;
 (1)、上述两种解决思路都可以证明一组三角形全等,判定一个四边形为平行四边形,从而可证得线段之间满足的数量关系式为 .(2)、【类比探究】
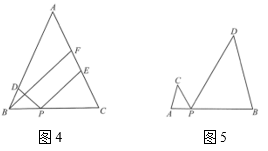
(1)、上述两种解决思路都可以证明一组三角形全等,判定一个四边形为平行四边形,从而可证得线段之间满足的数量关系式为 .(2)、【类比探究】如图4,在等腰中, , 点D、E分别是边上的点,点P是底边上的点,且 , 过点B作交于点F,请写出线段之间满足的数量关系式,并说明理由.
(3)、 【拓展应用】如图5,在与中, , , 点A、B、P在同一条直线上,若 , , 则 .