2024年广东省深圳市七年级下册数学期末模拟试卷(三)
试卷更新日期:2024-05-24 类型:期末考试
一、选择题(本大题共10小题,每小题3分,共30分,每小题有四个选项,只有一个是正确的)
-
1. 小篆,是在秦始皇统一六国后创制的汉字书写形式.下列四个小篆字中为轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 计算a2•a5的结果是( )A、a10 B、a7 C、a3 D、a83. 1986年9月,深圳市评选簕杜鹃为深圳市市花,簕杜鹃又名三角梅、九重葛。簕杜鹃属于紫茉莉科叶子花属的藤状灌木,具有旺盛的生命力和较长的花期,它的苞片大而美丽,颜色鲜艳,给人以奔放、热烈的感受。簕杜鹃的单粒的花粉粒直径约为 , 数据0.000015用科学记数法表示为( )A、 B、 C、 D、4. 抛掷一枚质地均匀的正方体骰子,骰子各面分别标有数字1、2、3、4、5、6,则出现朝上的数字小于3的概率是( )A、 B、 C、 D、5. 若完全平方式 , 则( )A、30 B、 C、25 D、106. 如图,下列推理错误的是( )
2. 计算a2•a5的结果是( )A、a10 B、a7 C、a3 D、a83. 1986年9月,深圳市评选簕杜鹃为深圳市市花,簕杜鹃又名三角梅、九重葛。簕杜鹃属于紫茉莉科叶子花属的藤状灌木,具有旺盛的生命力和较长的花期,它的苞片大而美丽,颜色鲜艳,给人以奔放、热烈的感受。簕杜鹃的单粒的花粉粒直径约为 , 数据0.000015用科学记数法表示为( )A、 B、 C、 D、4. 抛掷一枚质地均匀的正方体骰子,骰子各面分别标有数字1、2、3、4、5、6,则出现朝上的数字小于3的概率是( )A、 B、 C、 D、5. 若完全平方式 , 则( )A、30 B、 C、25 D、106. 如图,下列推理错误的是( )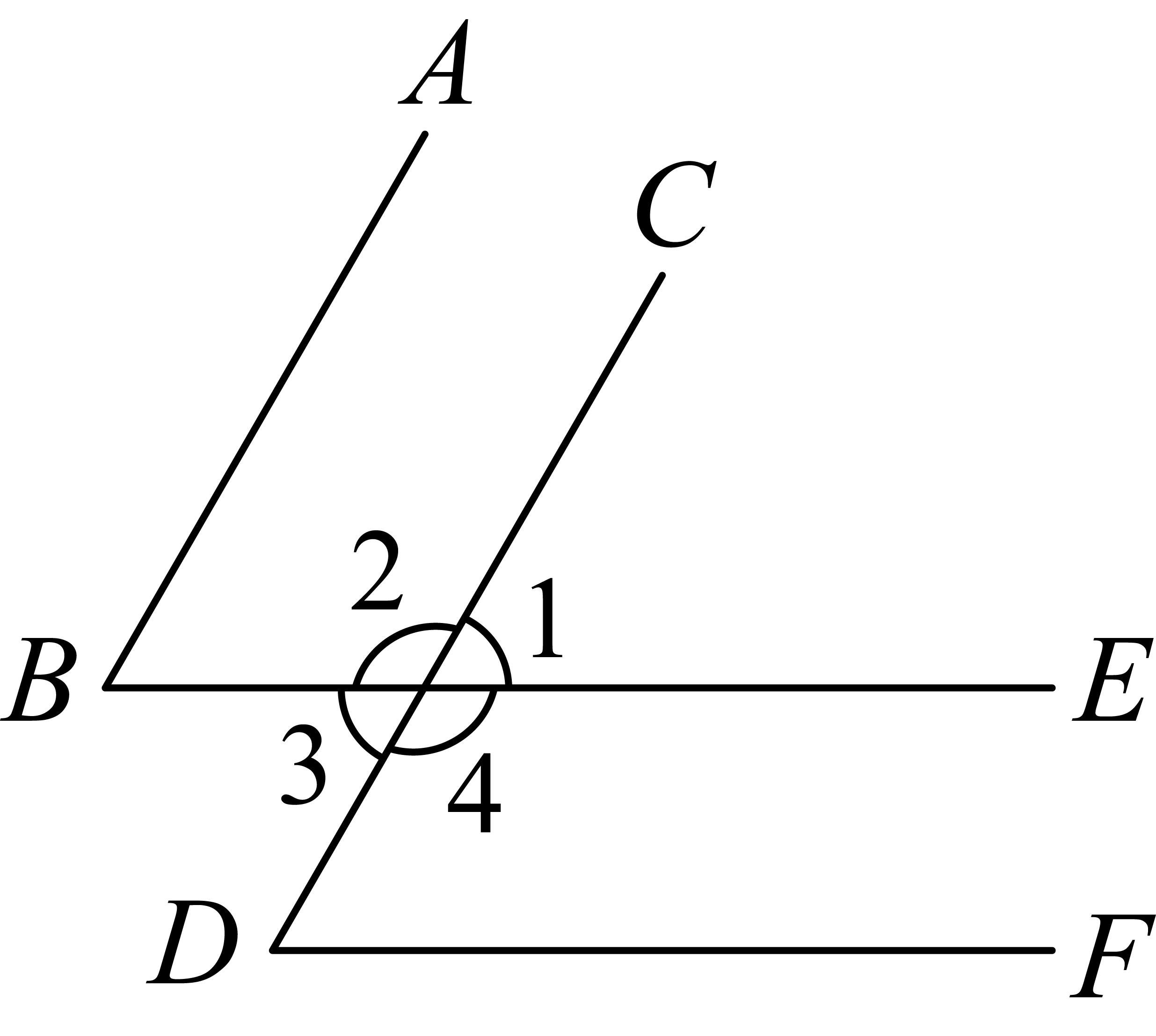 A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 下列实际情境中的变量关系可以用如图近似地刻画的是( )
A、若 , 则 B、若 , 则 C、若 , 则 D、若 , 则7. 下列实际情境中的变量关系可以用如图近似地刻画的是( )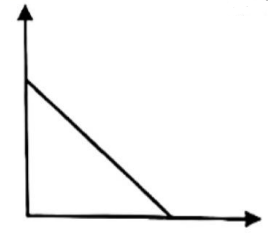 A、匀速骑行的自行车(速度与时间的关系) B、篮球运动员投出去的篮球(高度与时间的关系) C、燃烧的蜡烛(蜡烛长度与时间的关系) D、早晨升旗仪式(国旗高度与时间的关系)8. 用三角板作的高,下列作法正确的是( )A、
A、匀速骑行的自行车(速度与时间的关系) B、篮球运动员投出去的篮球(高度与时间的关系) C、燃烧的蜡烛(蜡烛长度与时间的关系) D、早晨升旗仪式(国旗高度与时间的关系)8. 用三角板作的高,下列作法正确的是( )A、 B、
B、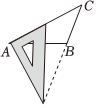 C、
C、 D、
D、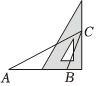 9. 若一个角的补角是这个角余角的4倍,则这个角是( )A、30° B、45° C、60° D、90°10.
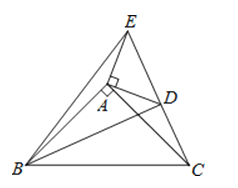
9. 若一个角的补角是这个角余角的4倍,则这个角是( )A、30° B、45° C、60° D、90°10.已知:如图,在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②∠ACE+∠DBC=45°;③BD⊥CE;④∠BAE+∠DAC=180°.
其中结论正确的个数是( )
 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题(本题有5小题,每小题3分,共15分)
-
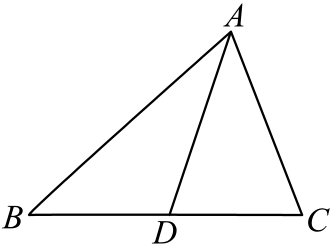
11. 计算: .12. 如图,在中,是边上的中线,若 , , 则点D到的距离为 .
 13. 若n满足 , 则等于 .14. 小颖准备乘出租车到距家超过3km的科技馆参观,出租车的收费标准如下:
13. 若n满足 , 则等于 .14. 小颖准备乘出租车到距家超过3km的科技馆参观,出租车的收费标准如下:里程数/km
收费/元
3km以内(含3km)
8.00
3km以外每增加1km
1.80
则小颖应付车费y(元)与行驶里程数x(km)之间的关系式为 .
15. 如图,已知 , , 点E、F在线段上,且满足平分 , 平分 , 可以左右平行移动.给出下列四个结论.其中正确的结论有(填写所有正确结论的序号).
①;
②;
③;
④
三、解答题(共7题,共55分)
-
16. 计算:(1)、(2)、17. 先化简,再求值: , 其中 ,18.
尺规作图,已知线段 、线段 和∠ ,用直尺和圆规作△ABC,使BC= ,AB= ,∠ABC=∠ 。(要求画出图形,并保留作图痕迹,不必写作法)
 19. 如图, 长 , 宽 的大长方形被分割成 9 小块, 除阴影 外, 其余 7 块是形状、大小完全相同的小长方形,其中较短一边长为 .
19. 如图, 长 , 宽 的大长方形被分割成 9 小块, 除阴影 外, 其余 7 块是形状、大小完全相同的小长方形,其中较短一边长为 . (1)、 从图可知, 每个小长方形较长一边长为 (用含 的代数式表示).(2)、 分别用含 的代数式表示阴影 的面积.(3)、若阴影 与阴影 的面积差不会随着 的变化而变化, 请求出 的取值, 并说明理由.20. 【项目学习】“我们把多项式a2+2ab+b2及a2―2ab+b2叫做完全平方式”.
(1)、 从图可知, 每个小长方形较长一边长为 (用含 的代数式表示).(2)、 分别用含 的代数式表示阴影 的面积.(3)、若阴影 与阴影 的面积差不会随着 的变化而变化, 请求出 的取值, 并说明理由.20. 【项目学习】“我们把多项式a2+2ab+b2及a2―2ab+b2叫做完全平方式”.如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式中出现完全平方式,再减去这个项,使整个式的值不变,这种方法叫做配方法,配方法是一种重要的解决问题的数学方法.例如:求当a取何值,代数式a2+6a+8有最小值?最小值是多少?
解:a2+6a+8=a2+6a+32—32+8=(a+3)2—1
因为(a+3)2≥0,所以a2+6a+8≥—1,
因此,当a=―3时,代数式α2+6a+8有最小值,最小值是-1.
(1)、【问题解决】利用配方法解决下列问题:①当x=时,代数式x2—2x一1有最小值,最小值为.
②当x取何值时,代数式2x2+8x+12有最小值?最小值是多少?
(2)、【拓展提高】③当x,y何值时,代数式5x2—4xy+y2+6x+25取得最小值,最小值为多少?
④如图所示的第一个长方形边长分别是2α十5、3α十2,面积为S1;如图所示的第二个长方形边长分别是5a、a+5,面积为S2 . 试比较S1与S2的大小,并说明理由.
 21. 如图
21. 如图 (1)、【探究与发现】如图1,是的中线,延长至点E,使 , 连接 , 写出图中全等的两个三角形 .(2)、【理解与应用】填空:如图2,是的中线,若 , , 设 , 则x的取值范围是 .(3)、已知:如图3,是的中线, , 点Q在的延长线上, , 求证: .22. 综合与实践
(1)、【探究与发现】如图1,是的中线,延长至点E,使 , 连接 , 写出图中全等的两个三角形 .(2)、【理解与应用】填空:如图2,是的中线,若 , , 设 , 则x的取值范围是 .(3)、已知:如图3,是的中线, , 点Q在的延长线上, , 求证: .22. 综合与实践问题情境:“综合与实践”课上,老师将一副直角三角板摆放在直线MN上(如图1,).保持三角板EDC不动,老师将三角板ABC绕点以每秒的速度顺时针旋转,旋转时间为秒,当AC与射线CN重合时停止旋转.各小组解决老师给出的问题,又提出新的数学问题,请你解决这些问题.
深入探究:
 (1)、老师提出,如图2,当AC转到与∠DCE的角平分线重合时,∠ECB-∠DCA=15°,当AC转到与的角平分线重合时, , 当AC在内部的其他位置时,结论是否依然成立?请说明理由.(2)、勤学小组提出:若AC旋转至的外部,与是否还存在如上数量关系?若存在,请说明理由;若不存在,请写出与的数量关系,并说明理由.(3)、拓展提升:
(1)、老师提出,如图2,当AC转到与∠DCE的角平分线重合时,∠ECB-∠DCA=15°,当AC转到与的角平分线重合时, , 当AC在内部的其他位置时,结论是否依然成立?请说明理由.(2)、勤学小组提出:若AC旋转至的外部,与是否还存在如上数量关系?若存在,请说明理由;若不存在,请写出与的数量关系,并说明理由.(3)、拓展提升:智慧小组提出:若AC旋转到与射线CM重合时停止旋转.在旋转过程中,直线DE与直线AC是否存在平行的位置关系?若存在,请直接写出的值;若不存在,请说明理由.