2024年广东省深圳市七年级下册数学期末模拟试卷(二)
试卷更新日期:2024-05-24 类型:期末考试
一、选择题
-
1. 下列计算正确的是( )A、x8÷x4=x2 B、x3•x4=x12 C、(x3)2=x6 D、(﹣x2y3)2=﹣x4y62. 2023年10月26日神舟十七号载人飞船在酒泉卫星发射中心圆满发射成功.此次神舟十七号载人飞船航天员空间站还将进行一系列科学实验,包括“空间蛋白质分子组装与应用研究”.其中某一蛋白质分子的直径仅0.000000028米,这个数用科学记数法表示为( )A、 B、 C、 D、3. 如果多项式是一个完全平方式,则的值是( )A、4 B、 C、8 D、4. 下列图形能够直观地解释的是( )A、
 B、
B、 C、
C、 D、
D、 5. 多项式 , 则( )A、6 B、 C、8 D、6. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P , 点F为焦点.若∠1=x°,∠2=y°,则∠3的度数为( )
5. 多项式 , 则( )A、6 B、 C、8 D、6. 如图,一束平行于主光轴的光线经凸透镜折射后,其折射光线与一束经过光心O的光线相交于点P , 点F为焦点.若∠1=x°,∠2=y°,则∠3的度数为( )
 A、(x﹣y)° B、(180﹣x﹣y)° C、(180﹣x+y)° D、(x+y﹣90)°7. 吴老师在演示概率试验时,连续随机抛掷一枚质地均匀的骰子,前3次的结果是“6”,则第4次的结果是“6”的概率是( )A、0 B、 C、 D、18. 小明家有一本200页的故事书,已知他每小时能看50页,星期天上午小明先看了故事书的一半后又做了一个小时的作业,然后他才继续看完这本书.下列能体现这本书剩下的页数y(页)与时间t(时)之间关系的是( )A、
A、(x﹣y)° B、(180﹣x﹣y)° C、(180﹣x+y)° D、(x+y﹣90)°7. 吴老师在演示概率试验时,连续随机抛掷一枚质地均匀的骰子,前3次的结果是“6”,则第4次的结果是“6”的概率是( )A、0 B、 C、 D、18. 小明家有一本200页的故事书,已知他每小时能看50页,星期天上午小明先看了故事书的一半后又做了一个小时的作业,然后他才继续看完这本书.下列能体现这本书剩下的页数y(页)与时间t(时)之间关系的是( )A、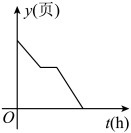 B、
B、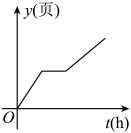 C、
C、 D、
D、 9. 下列说法中正确的是( )
9. 下列说法中正确的是( )①角平分线上任意一点到角的两边的距离相等;
②等腰三角形两腰上的高相等;
③等腰三角形的中线也是它的高;
④线段垂直平分线上的点(不在这条线段上)与这条线段两个端点构成等腰三角形
A、①②③④ B、①②③ C、①②④ D、②③④10. 如图,ABC的三条边相等,三个内角也相等,且 , 连接DE,DF,EF,CD与BE交于H点,以下结论:①;②BDE与CFD的面积相等;③;④ . 其中正确的是( )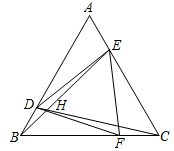 A、①②③④ B、①② C、②③④ D、③④
A、①②③④ B、①② C、②③④ D、③④二、填空题(本题有5小题,每小题3分,共15分)
-
11. 若 , 则的结果是 .12. 等腰三角形的一个内角是 , 则它底角的度数是 .13. “四时花竞巧,九子粽争新”,端午节吃粽子是我国的传统习俗.小佩的妈妈准备了形状大小一样的豆沙粽3个、红枣粽4个、腊肉粽2个,板栗粽3个,其中腊肉粽是咸粽,其它粽是甜粽.小佩随机选一个,选到咸粽的概率是 .14. 某市区出租车的收费标准是起步价元(行程小于或等于千米),超过千米每增加千米(不足千米按千米计算)加收元,则出租车费(元)与行程(千米)()之间的关系式为 .15. 如图,在中, , , D、E分别在、上,将沿折叠得 , 且满足 , 则.

三、解答题(共7题,共55分)
-
16. 计算:(1)、(2)、(用整式乘法公式计算).17. 先化简,再求值; , 其中 .18. 如图,∠AOB

(画图时不要求写出画法,但要保留画图痕迹)
(1)、用尺规作出∠AOB的平分线OD.(2)、以OA为一边在∠AOB的外部画,∠AOB的余角∠AOC.19. 如图,已知是的平分线,交于点F , D、E、G分别是、、上的点,且 , (1)、图中与是一对 , 与是一对 , 与是一对 . (填“同位角”或“内错角”或“同旁内角”)(2)、判断与是什么位置关系?说明理由;(3)、若 , 垂足为F , , 求的度数20. 由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”为了测定某种型号小型载客汽车的刹车性能车速不超过 , 对这种型号的汽车进行了测试,测得的数据如下表:
(1)、图中与是一对 , 与是一对 , 与是一对 . (填“同位角”或“内错角”或“同旁内角”)(2)、判断与是什么位置关系?说明理由;(3)、若 , 垂足为F , , 求的度数20. 由于惯性的作用,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”为了测定某种型号小型载客汽车的刹车性能车速不超过 , 对这种型号的汽车进行了测试,测得的数据如下表:刹车时车速
刹车距离
请回答下列问题:
(1)、在这个变化过程中,自变量是 , 因变量是;(2)、当刹车时车速为时,刹车距离是;(3)、根据上表反映的规律写出该种型号汽车与之间的关系式:;(4)、该型号汽车在高速公路上发生了一次交通事故,现场测得刹车距离为 , 推测刹车时车速是多少?并说明事故发生时,汽车是超速行驶还是正常行驶?相关法规:道路交通安全法第七十八条:高速公路上行驶的小型载客汽车最高车速不得超过每小时公里
21. 【项目学习】配方法是数学中重要的一种思想方法,它是指将一个式子的某部分通过恒等变形化为完全平方式或几个完全平方式的和的方法,这种方法常被用到代数式的变形中,并结合非负数的意义来解决一些问题.例如,把二次三项式进行配方
解:
我们定义:一个整数能表示成(a,b是整数)的形式,则称这个数为“完美数”例如,5是“完美数”,理由:因为 , 再如, , (x,y是整数)所以M也是“完美数”
(1)、【问题解决】下列各数中,“完美数”有 . (填序号)
①10 ②45 ③28 ④29
(2)、若二次三项式(是整数)是“完美数”,可配方成(m,为常数),则的值为;(3)、【问题探究】已知(x,y是整数,k是常数),要使S为“完美数”,试求出符合条件的k的值.
(4)、【问题拓展】已知实数x,y满足 , 求的最小值.
22. 如图 (1)、问题发现:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,我们把具有这种规律的图形称为“手拉手”图形,
(1)、问题发现:两个顶角相等的等腰三角形,如果具有公共的顶角的顶点,并把它们的底角顶点连接起来,则形成一组全等的三角形,我们把具有这种规律的图形称为“手拉手”图形,如图1,和ΔADE是顶角相等的等腰三角形,即 , , 且 , 分别连接 , . 求证:;
(2)、类比探究:如图2,和ΔADE都是等腰三角形,即 , , 且 , B,C,D在同一条直线上.请判断线段与存在怎样的数量关系及位置关系,并说明理由.(3)、问题解决:如图3,若ΔACB和ΔDCE均为等腰直角三角形,且CA=CB,CD=CE,∠ACB=∠DCE=90°,点A,D,E在同一条直线上,CM为ΔDCE中DE边上的高,连接BE,若AE=7,BE=2,请直接写出CM的长,不说明理由.