2024年广东省深圳市七年级下册数学期末模拟试卷(一)

试卷更新日期：2024-05-24 类型：期末考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分，每小题有四个选项，只有一个是正确的）

1. 下列运算正确的是（）

A、 $a^{3} + a^{3} = a^{6}$ B、 $a^{2} \cdot a^{3} = a^{6}$ C、 ${(- 3 a)}^{2} = - 6 a^{2}$ D、 $a^{2} \cdot {(- a)}^{2} = a^{4}$

查看试题解析
2. 某种冠状病毒的大小约为0.000125mm，该数用科学记数法表示正确的是（）

A、0.125×10^﹣3 B、0.125×10^﹣4 C、1.25×10^﹣3 D、1.25×10^﹣4

查看试题解析
3. 下列各式能用平方差公式计算的是（）

A、 $(x - y) (x - y)$ B、 $(2 x + y) (2 y - x)$ C、 $(x + 1) (x - 1)$ D、 $(x - 1) (1 - x)$

查看试题解析
4. 如图，下列条件不能判定 $A D ∥ E F$ 的是（）

A、 $∠ A = ∠ C B E$ B、 $∠ A + ∠ A B E = 180 °$ C、 $∠ D = ∠ D B E$ D、 $∠ D = ∠ C B E$

查看试题解析
5. 如图，点E、F分别为长方形纸片ABCD的边AB ， CD上的点，将长方形纸片沿EF翻折，点C ， B分别落在点C $’$ ， B $’$ 处．若∠DFC $’$ =a ，则∠FEA-∠AEB $’$ 的度数为（）

A、 $45 ° + \frac{1}{2} α$ B、 $60 ° - \frac{1}{2} α$ C、 $90 ° - \frac{1}{2} α$ D、 $90 ° - \frac{3}{2} α$

查看试题解析
6. 佳佳和爸爸一道从家出发，25min后走到离家1000m的公园，爸爸随即原速返回，她停留10min后返回，两人恰好同时到家，下列图象中，表示她离家后距离与时间关系的是（）

A、 B、 C、 D、

查看试题解析
7. 如图，AB=DB，∠1=∠2，请问添加下面哪个条件不能判断△ABC≌△DBE的是（）

A、BC=BE B、AC=DE C、∠A=∠D D、∠ACB=∠DEB

查看试题解析
8. 等腰三角形的一边长 $11 c m$ ，另一边长 $5 c m$ ，它的第三边长为（）

A、 $5 c m$ B、 $6 c m$ C、 $11 c m$ D、 $5 c m$ 或 $11 c m$

查看试题解析
9. 如图（1）所示为长方形纸带，将纸带沿EF折叠成图（2）；再沿BF折叠成图（3）；继续沿EF折叠成图（4）按此操作，最后一次折叠后恰好完全盖住∠EFG，整个过程共折叠了9次，问图（1）中∠DEF的度数是（）

A、20° B、19° C、18° D、15°

查看试题解析
10. 如图，△ABC和△BDE都是等边三角形，点A，B，D在一条直线上。给出4个结论：①AE=CD；②AB⊥FB；③∠AFC=60°；④△BGH是等边三角形。其中正确的是（）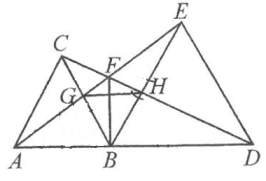

A、①，②，③ B、①，②，④ C、①，③，④ D、②，③，④

查看试题解析

二、填空题（本题有5小题，每小题3分，共15分）

11. 若 $x^{2} - 6 x + k$ 是一个完全平方式，则 $k =$ ．

查看试题解析
12. 如图，一块长为 $a c m$ ，宽为 $b c m$ 的长方形地板中间有一条裂痕(如图甲)，若把裂痕右边的一块向右平移 $1 c m$ (如图乙)，则产生的裂缝的面积是. $c m^{2}$ .

查看试题解析
13. 欢欢观察“抖空竹”时发现，可以将某一时刻的情形抽象成数学问题：如图，已知AB∥CD，∠BAE＝92°，∠DCE＝115°，则∠E的度数是°．

查看试题解析
14. 一个不透明的袋子里装有白球、黄球共32个，这些球除颜色外都相同，小明通过多次试验发现，摸出黄球的频率稳定在0.25左右，则袋子中白球的个数最有可能是个.

查看试题解析
15. 如图， $A D$ 、 $C D$ 、 $B D$ 分别平分 $△ A B C$ 的外角 $∠ E A C$ 、 $∠ A C F$ 、内角 $∠ A B C$ ，若 $∠ A B C = ∠ A C B$ ，以下结论： $① A D / / B C$ ； $② ∠ A D B = \frac{1}{2} ∠ A C B$ ； $③ ∠ A D C = 90 ° - \frac{1}{2} ∠ A C B$ ； $④ D B$ 平分 $∠ A D C$ ； $⑤ ∠ A B C + ∠ B D C = 90 ° .$ 其中正确的结论是 $($ 填序号 $)$ ．

查看试题解析

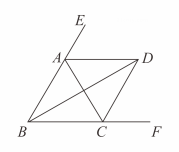
三、解答应（共7题，共55分）

16. 计算 $- 1^{2} + {(π - 3.14)}^{0} - {(- \frac{1}{3})}^{- 2} + {(- 2)}^{3}$ ．

查看试题解析
17. 先化简，再求值： $[(a - 2 b)^{2} - (a - 2 b) (a + 2 b) + 4 b^{2}] \div 2 b$ ，其中 $a = 1$ ， $b = 2$ ．

查看试题解析
18. 已知：线段a，∠α，∠β．
求作：△ABC，使BC＝a，∠B＝∠α，∠C＝∠β．

查看试题解析
19. 中国联通在某地的资费标准为包月186元时，超出部分国内拨打0.36元/分，由于业务多，小明的爸爸打电话已超出了包月费．
下表是超出部分国内拨打的收费标准
时间/分
1
2
3
4
5
…
电话费/元
0.36
0.72
1.08
1.44
1.8
…
（1）这个表反映了哪两个变量之间的关系？哪个是自变量？
（2）如果用x表示超出时间，y表示超出部分的电话费，那么y与x的表达式是什么？
（3）如果打电话超出25分钟，需付多少电话费？
（4）某次打电话的费用超出部分是54元，那么小明的爸爸打电话超出几分钟？

查看试题解析
20. 如图，在△ABC中，点D、F在BC边上，点E在AB边上，点G在AC边上，EF与GD的延长线交于点H ， $∠ 1 = ∠ B$ ， $∠ 2 + ∠ 3 = 180 °$ ．

(1)、判断EH和AD的位置关系，并说明理由；

(2)、若 $∠ D G C = 60 °$ ，且 $∠ H - ∠ 4 = 4 °$ ，求∠H的度数．

查看试题解析
21. 多项式乘法的学习中，等式 $(a + b) (c + d) = a c + a d + b c + b d$ 可以用平面图形（图 $1$ ）的面积来说明．

(1)、【初步探究】
请使用（图 $2$ ）的 $2$ 种规格的正方形，设计一个平面图形方案说明等式 ${(a + b)}^{2} = a^{2} + 2 a b + b^{2}$ 是正确的；

(2)、【知识拓展】
为进一步探索部分平面图形的面积与等式的关系，在某次数学活动中，准备（图 $3$ ）所示的三种规格的正方形、长方形卡片若干张．小明从中选取 $9$ 张，拼成一个边长为 $(a + b + c)$ 的正方形，请你写出与其面积相应的等式；

(3)、【延伸应用】
请利用（ $2$ ）中得到的等式解答以下问题：若实数 $x ， y$ ，满足 $x^{2} + 4 y^{2} + 9 z^{2} = 8$ ， $x + 2 y + 3 z = 4$ ，求 $2 x y + 3 x z + 6 y z$ 的值．

查看试题解析
22. 探究题：如图：

(1)、△ABC为等边三角形，动点D在边CA上，动点P在边BC上，若这两点分别从C、B点同时出发，以相同的速度由C向A和由B向C运动，连接AP，BD交于点Q，两点运动过程中AP=BD成立吗？请证明你的结论；

(2)、如果把原题中“动点D在边CA上，动点P边BC上，”改为“动点D，P在射线CA和射线BC上运动”，其他条
件不变，如图（2）所示，两点运动过程中∠BQP的大小保持不变．请你利用图（2）的情形，

求证：∠BQP=60°；

(3)、如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动，连接PD交BC于E”，其他条件不变，如图（3），则动点D，P在运动过程中，DE始终等于PE吗？写出证明过程．

查看试题解析

时间/分	1	2	3	4	5	…
电话费/元	0.36	0.72	1.08	1.44	1.8	…