2024年中考数学考前20天终极冲刺专题之几何综合
试卷更新日期:2024-05-23 类型:三轮冲刺
一、解答题
-
1.
 (1)、如图1,平分分别在射线上,若 , 求证:;(2)、如图2,在中,交边于点于点H . 已知 , 求的面积;(3)、如图3,在等边中,点D在边上,P为延长线上一点,E为边上一点,已知平分 , 求的长.2. 已知 , , , 点是边上一点,过点作于点 , 连接 , 点是中点,连接 , .
(1)、如图1,平分分别在射线上,若 , 求证:;(2)、如图2,在中,交边于点于点H . 已知 , 求的面积;(3)、如图3,在等边中,点D在边上,P为延长线上一点,E为边上一点,已知平分 , 求的长.2. 已知 , , , 点是边上一点,过点作于点 , 连接 , 点是中点,连接 , . (1)、如图①,线段 , 之间的数量关系为 , 的度数为;(2)、如图②,将绕点按顺时针方向旋转 , 请判断线段 , 之间的数量关系及的度数,并说明理由;(3)、若绕点旋转的过程中,当点落到直线上时,连接 , 若 , , 请直接写出的长.3. 如图1,在菱形中,对角线 , 相交于点 , , , 点为线段上的动点(不与点 , 重合),连接并延长交边于点 , 交的延长线于点 .
(1)、如图①,线段 , 之间的数量关系为 , 的度数为;(2)、如图②,将绕点按顺时针方向旋转 , 请判断线段 , 之间的数量关系及的度数,并说明理由;(3)、若绕点旋转的过程中,当点落到直线上时,连接 , 若 , , 请直接写出的长.3. 如图1,在菱形中,对角线 , 相交于点 , , , 点为线段上的动点(不与点 , 重合),连接并延长交边于点 , 交的延长线于点 . (1)、当点恰好为的中点时,求证:;(2)、求线段的长;(3)、当为直角三角形时,求的值;(4)、如图2,作线段的垂直平分线,交于点 , 交于点 , 连接 , 在点的运动过程中,的度数是否为定值?如果是,求出这个定值;如果不是,请说明理由.4. 已知在中, , , , 以边为直径作 , 与边交于点 , 点为边的中点,连接 .
(1)、当点恰好为的中点时,求证:;(2)、求线段的长;(3)、当为直角三角形时,求的值;(4)、如图2,作线段的垂直平分线,交于点 , 交于点 , 连接 , 在点的运动过程中,的度数是否为定值?如果是,求出这个定值;如果不是,请说明理由.4. 已知在中, , , , 以边为直径作 , 与边交于点 , 点为边的中点,连接 .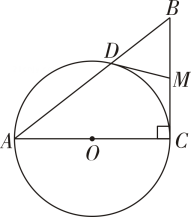 (1)、求证:是的切线;(2)、点为直线上任意一动点,连接交于点 , 连接 .
(1)、求证:是的切线;(2)、点为直线上任意一动点,连接交于点 , 连接 .当时,求的长;
求的最大值.
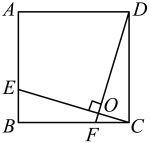
5. 已知内接于 , 为的直径,N为的中点,连接交于点H .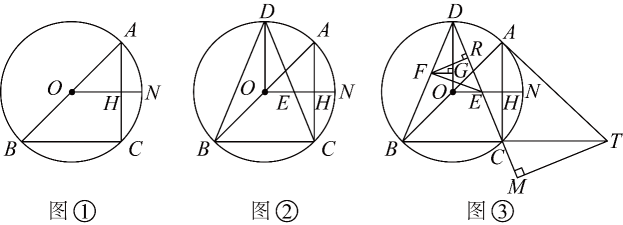 (1)、如图①,求证;(2)、如图②,点D在上,连接 , , , 交于点E , 若 , 求证;(3)、如图③,在(2)的条件下,点F在上,过点F作 , 交于点G . , 过点F作 , 垂足为R , 连接 , , , 点T在的延长线上,连接 , 过点T作 , 交的延长线于点M , 若 , 求的长.6. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .
(1)、如图①,求证;(2)、如图②,点D在上,连接 , , , 交于点E , 若 , 求证;(3)、如图③,在(2)的条件下,点F在上,过点F作 , 交于点G . , 过点F作 , 垂足为R , 连接 , , , 点T在的延长线上,连接 , 过点T作 , 交的延长线于点M , 若 , 求的长.6. 小王在学习浙教版九上课本第72页例2后,进一步开展探究活动:将一个矩形ABCD绕点A顺时针旋转α(0°<α≤90°),得到矩形AB′C′D′,连结BD .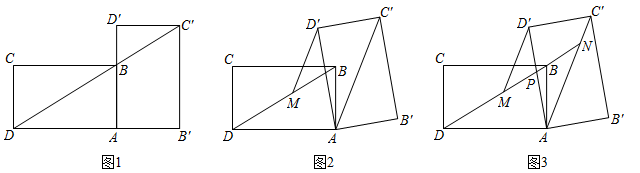
[探究1]如图1,当α=90°时,点C′恰好在DB延长线上.若AB=1,求BC的长.
[探究2]如图2,连结AC′,过点D′作D′M∥AC′交BD于点M . 线段D′M与DM相等吗?请说明理由.
[探究3]在探究2的条件下,射线DB分别交AD′,AC′于点P , N(如图3),发现线段DN , MN , PN存在一定的数量关系,请写出这个关系式,并加以证明.
7.已知正方形 的对角线 , 相交于点 .
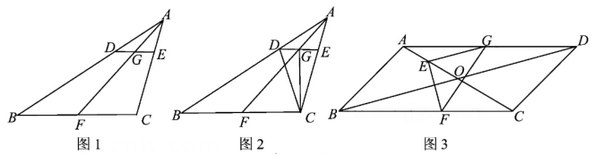
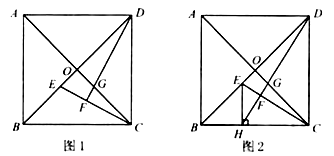 (1)、如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;(2)、如图2, 是 上的点,过点 作 ,交线段 于点 ,连结 交 于点 ,交 于点 .若 ,
(1)、如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;(2)、如图2, 是 上的点,过点 作 ,交线段 于点 ,连结 交 于点 ,交 于点 .若 ,①求证: ;
②当 时,求 的长.
二、实践探究题
-
8. 已知正方形ABCD,E为对角线AC上一点.

① ② ③(1)、【建立模型】如图①所示,连接BE,DE.求证:BE=DE;
(2)、【模型应用】如图②所示,F是DE延长线上一点,EF交AB于点G,FB⊥BE,判断△FBG的形状,并说明理由;
(3)、【模型迁移】如图③所示,F是DE延长线上一点,EF交AB于点G,FB⊥BE,BE=BF,求证:GE=(-1)DE.
9. 【问题呈现】和都是直角三角形, , 连接 , , 探究 , 的位置关系.
 (1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】
(1)、如图1,当时,直接写出 , 的位置关系:;(2)、如图2,当时,(1)中的结论是否成立?若成立,给出证明;若不成立,说明理由.(3)、【拓展应用】当时,将绕点C旋转,使三点恰好在同一直线上,求的长.
10. (1)、【特例感知】
(1)、【特例感知】如图1,在正方形ABCD中,点P在边AB的延长线上,连结PD , 过点D作DM⊥PD , 交BC的延长线于点M . 求证:△DAP≌△DCM .
(2)、【变式求异】如图2,在Rt△ABC中,∠ABC=90°,点D在边AB上,过点D作DQ⊥AB , 交AC于点Q , 点P在边AB的延长线上,连结PQ , 过点Q作QM⊥PQ , 交射线BC于点M . 已知BC=8,AC=10,AD=2DB , 求的值.
(3)、【拓展应用】如图3,在Rt△ABC中,∠BAC=90°,点P在边AB的延长线上,点Q在边AC上(不与点A , C重合),连结PQ , 以Q为顶点作∠PQM=∠PBC , ∠PQM的边QM交射线BC于点M . 若AC=mAB , CQ=nAC(m , n是常数),求的值(用含m , n的代数式表示).
11. 【问题背景】人教版八年级下册数学教材第63页“实验与探究”问题1如下:如图,正方形的对角线相交于点 , 点又是正方形的一个顶点,而且这两个正方形的边长相等,无论正方形绕点怎样转动,两个正方形重叠部分的面积,总等于一个正方形面积的 . 想一想,这是为什么?(此问题不需要作答)
九年级数学兴趣小组对上面的问题又进行了拓展探究、内容如下:正方形的对角线相交于点 , 点落在线段上,为常数).
 (1)、【特例证明】
(1)、【特例证明】如图1,将的直角顶点与点重合,两直角边分别与边 , 相交于点 , .
①填空: ▲ ;
②求证: . (提示:借鉴解决【问题背景】的思路和方法,可直接证明;也可过点分别作 , 的垂线构造全等三角形证明.请选择其中一种方法解答问题②.
(2)、【类比探究】如图2,将图1中的沿方向平移,判断与的数量关系(用含的式子表示),并说明理由.
(3)、【拓展运用】如图3,点在边上, , 延长交边于点 , 若 , 求的值.
12. 【问题情境】如图,在中, , . 点D在边上将线段绕点D顺时针旋转得到线段(旋转角小于),连接 , , 以为底边在其上方作等腰三角形 , 使 , 连接 .(1)、【尝试探究】如图1,当时,易知;
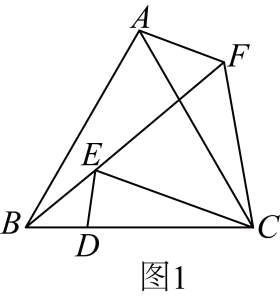
如图2,当时,则与的数量关系为;
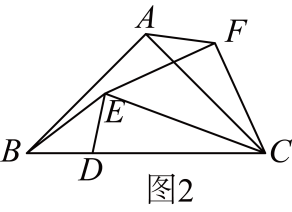 (2)、如图3,写出与的数量关系(用含α的三角函数表示).并说明理由;
(2)、如图3,写出与的数量关系(用含α的三角函数表示).并说明理由; (3)、【拓展应用】
(3)、【拓展应用】如图4,当 , 且点B , E , F三点共线时.若 , , 请直接写出的长.
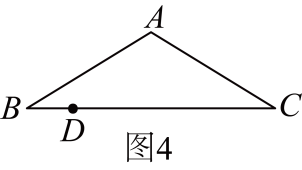 13. 【阅读理解】如图1,在矩形中,若 , 由勾股定理,得 , 同理 , 故 .
13. 【阅读理解】如图1,在矩形中,若 , 由勾股定理,得 , 同理 , 故 . (1)、【探究发现】如图2,四边形为平行四边形,若 , 则上述结论是否依然成立?请加以判断,并说明理由.
(1)、【探究发现】如图2,四边形为平行四边形,若 , 则上述结论是否依然成立?请加以判断,并说明理由. (2)、【拓展提升】如图3,已知为的一条中线, . 求证: .
(2)、【拓展提升】如图3,已知为的一条中线, . 求证: . (3)、【尝试应用】如图4,在矩形中,若 , 点P在边上,则的最小值为 .
(3)、【尝试应用】如图4,在矩形中,若 , 点P在边上,则的最小值为 . 14. 综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点, ,EP与正方形的外角 的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;
14. 综合与实践,【问题情境】:数学活动课上,老师出示了一个问题:如图1,在正方形ABCD中,E是BC的中点, ,EP与正方形的外角 的平分线交于P点.试猜想AE与EP的数量关系,并加以证明;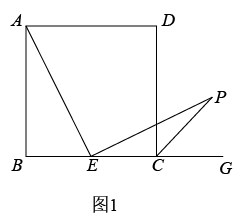
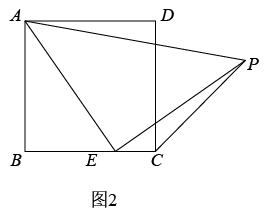
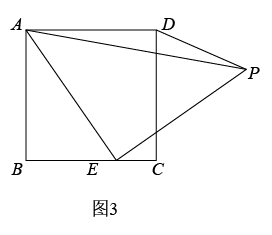 (1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.15.(1)、【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证:
(1)、【思考尝试】同学们发现,取AB的中点F,连接EF可以解决这个问题.请在图1中补全图形,解答老师提出的问题.(2)、【实践探究】希望小组受此问题启发,逆向思考这个题目,并提出新的问题:如图2,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接CP,可以求出 的大小,请你思考并解答这个问题.(3)、【拓展迁移】突击小组深入研究希望小组提出的这个问题,发现并提出新的探究点:如图3,在正方形ABCD中,E为BC边上一动点(点E,B不重合), 是等腰直角三角形, ,连接DP.知道正方形的边长时,可以求出 周长的最小值.当 时,请你求出 周长的最小值.15.(1)、【探究发现】如图①所示,在正方形中,为边上一点,将沿翻折到处,延长交边于点.求证: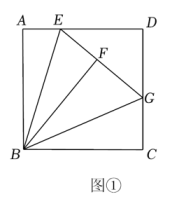 (2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长.
(2)、【类比迁移】如图②,在矩形中,为边上一点,且将沿翻折到处,延长交边于点延长交边于点且求的长. (3)、【拓展应用】如图③,在菱形中,为边上的三等分点,AB=6,将沿翻折得到 , 直线交于点求的长.
(3)、【拓展应用】如图③,在菱形中,为边上的三等分点,AB=6,将沿翻折得到 , 直线交于点求的长. 16. 华师版八年级下册数学教材第121页习题19.3第2小题及参考答案.
16. 华师版八年级下册数学教材第121页习题19.3第2小题及参考答案.2.如图,在正方形ABCD中,.求证:.
证明:设CE与DF交于点O,
∵四边形ABCD是正方形,
∴ , .
∴.
∵ ,
∴.
∴.
∴.
∴.
∴.
某数学兴趣小组在完成了以上解答后,决定对该问题进一步探究
(1)、【问题探究】如图,在正方形ABCD中,点E、F、G、H分别在线段AB、BC、CD、DA上,且.试猜想的值,并证明你的猜想. (2)、【知识迁移】如图,在矩形ABCD中, , , 点E、F、G、H分别在线段AB、BC、CD、DA上,且.则.
(2)、【知识迁移】如图,在矩形ABCD中, , , 点E、F、G、H分别在线段AB、BC、CD、DA上,且.则. (3)、【拓展应用】如图,在四边形ABCD中, , , , 点E、F分别在线段AB、AD上,且.求的值.
(3)、【拓展应用】如图,在四边形ABCD中, , , , 点E、F分别在线段AB、AD上,且.求的值. 17.
17. (1)、【基础巩固】
(1)、【基础巩固】
如图1,在△ABC中,D,E,F分别为AB,AC,BC上的点,DE∥BC,BF=CF,AF交DE于点G,求证:DG= EG.(2)、【尝试应用】
如图2,在(1)的条件下,连结CD,CG.若CG⊥DE,CD=6,AE=3,求 的值.(3)、【拓展提高】
如图3,在▱ABCD中,∠ADC=45°,AC与BD交于点O,E为AO上一点,EG∥BD交AD于点G,EF⊥EG交BC于点F.若∠EGF=40°,FG平分∠EFC,FG=10,求BF的长.
18. 如图, (1)、【推理】
(1)、【推理】
如图1,在正方形ABCD中,点E是CD上一动点,将正方形沿着BE折叠,点C落在点F处,连结BE,CF,延长CF交AD于点G. 求证: .(2)、【运用】
如图2,在(推理)条件下,延长BF交AD于点H.若 , ,求线段DE的长.(3)、【拓展】
将正方形改成矩形,同样沿着BE折叠,连结CF,延长CF,BF交直线AD于G,两点,若 , ,求 的值(用含k的代数式表示).19. 如图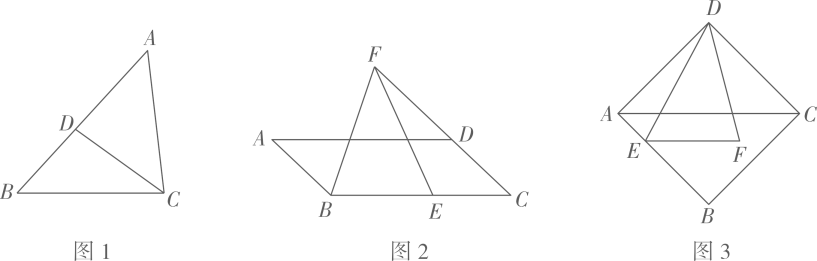 (1)、【基础巩固】
(1)、【基础巩固】如图1,在△ABC中,D为AB上一点,∠ACD=∠B.求证: .
(2)、【尝试应用】如图2,在 中,E为BC上一点,F为CD延长线上一点,∠BFE=∠A.若BF=4,BE=3,求AD的长.
(3)、【拓展提高】如图3,在菱形ABCD中,E是AB上一点,F是△ABC内一点,EF∥AC,AC=2EF, ,AE=2,DF=5,求菱形ABCD的边长.
三、综合题
-
20. 如图,在平面直角坐标系中,点M是第一象限内一点,过M的直线分别交x轴,y轴的正半轴于A,B两点,且M是AB的中点.以OM为直径的⊙P分别交x轴,y轴于C,D两点,交直线AB于点E(位于点M右下方),连结DE交OM于点K.
 (1)、若点M的坐标为(3,4),
(1)、若点M的坐标为(3,4),①求A,B两点的坐标;
②求ME的长.
(2)、若 =3,求∠OBA的度数.(3)、设tan∠OBA=x(0<x<1), =y,直接写出y关于x的函数解析式.21.(1)、[问题探究]如图1,在正方形中,对角线相交于点O.在线段上任取一点P(端点除外),连接 .
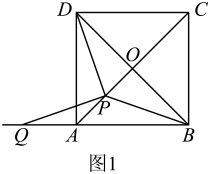
①求证:;
②将线段绕点P逆时针旋转,使点D落在的延长线上的点Q处.当点P在线段上的位置发生变化时,的大小是否发生变化?请说明理由;
③探究与的数量关系,并说明理由.
(2)、[迁移探究]如图2,将正方形换成菱形 , 且 , 其他条件不变.试探究与的数量关系,并说明理由.
 22. 如图1,点为等边的重心,点为边的中点,连接并延长至点 , 使得 , 连接 , , ,
22. 如图1,点为等边的重心,点为边的中点,连接并延长至点 , 使得 , 连接 , , , (1)、求证:四边形为菱形.(2)、如图2,以点为圆心,为半径作
(1)、求证:四边形为菱形.(2)、如图2,以点为圆心,为半径作①判断直线与的位置关系,并予以证明.
②点为劣弧上一动点(与点、点不重合),连接并延长交于点 , 连接并延长交于点 , 求证:为定值.
23. 综合与实践问题背景
数学小组发现国旗上五角星的五个角都是顶角为的等腰三角形,对此三角形产生了极大兴趣并展开探究.

探究发现
如图1,在中, , .
 (1)、操作发现:将折叠,使边落在边上,点的对应点是点 , 折痕交于点 , 连接 , , 则 , 设 , , 那么(用含的式子表示);(2)、进一步探究发现: , 这个比值被称为黄金比.在(1)的条件下试证明:;
(1)、操作发现:将折叠,使边落在边上,点的对应点是点 , 折痕交于点 , 连接 , , 则 , 设 , , 那么(用含的式子表示);(2)、进一步探究发现: , 这个比值被称为黄金比.在(1)的条件下试证明:;拓展应用:
当等腰三角形的底与腰的比等于黄金比时,这个三角形叫黄金三角形.例如,图1中的是黄金三角形.如图2,在菱形中, , . 求这个菱形较长对角线的长.
 (3)、拓展应用:
(3)、拓展应用:当等腰三角形的底与腰的比等于黄金比时,这个三角形叫黄金三角形.例如,图1中的是黄金三角形.如图2,在菱形中, , . 求这个菱形较长对角线的长.
 24. 综合与实践.
24. 综合与实践. (1)、提出问题如图 , 在和中, , 且 , , 连接 , 连接交的延长线于点 .
(1)、提出问题如图 , 在和中, , 且 , , 连接 , 连接交的延长线于点 .的度数是 .
: .
(2)、类比探究如图 , 在和中, , 且 , , 连接、并延长交于点 .的度数是 ;
: .
(3)、问题解决如图 , 在等边中,于点 , 点在线段上不与重合 , 以为边在的左侧构造等边 , 将绕着点在平面内顺时针旋转任意角度如图 , 为的中点,为的中点.说明为等腰三角形.
求的度数.