2024年中考数学考前20天终极冲刺专题之新定义问题

试卷更新日期：2024-05-22 类型：三轮冲刺

进入出卷网下载

一、选择题

1. 定义一种新运算 $a * b = - a b$ ，那么 $(m - n) * m$ 的运算结果为（）

A、 $m^{2} - m n$ B、 $- m^{2} + m n$ C、 $- m^{2} - m n$ D、 $m^{2} - n$

查看试题解析
2. 定义新运算： $a * b = \frac{\sqrt{a + b}}{a - b} (a \neq b$ 且 $a + b > 0)$ ，则 $6 * (6 * 3)$ 的值为（）

A、1 B、 $\frac{\sqrt{7}}{5}$ C、 $\sqrt{7}$ D、 $\frac{7}{5}$

查看试题解析
3. 定义一种新运算： $a & b = {\begin{array}{l} 4 a b - b^{2} (a > b) \\ a b + a - b (a < b) \end{array}$ ，则 $(1 & 4) & (- 1)$ 的值为（）

A、3 B、 $- 3$ C、5 D、 $- 5$

查看试题解析
4. 定义新运算： $m \oplus n = - \frac{n}{m} (m \neq 0)$ ，则对于函数 $y = x \oplus 2$ ，下列说法正确的是（）

A、当 $x < 0$ 时， $y$ 随 $x$ 增大而增大 B、该函数图象经过点 $(2 ， 1)$ C、该函数图象位于第一、三象限 D、当 $- 2 < x < - 1$ 时， $- 2 < y < - 1$

查看试题解析
5. 定义新运算： $p \oplus q = {\begin{array}{l} \frac{p}{q} (q > 0) ， \\ - \frac{p}{q} (q < 0) ， \end{array}$ 例如 $3 \oplus 5 =$ $\frac{3}{5} ， 3 \oplus (- 5) = \frac{3}{5}$ ，则 $y = 2 \oplus x (x \neq 0)$ 的图像可能是（）

A、 B、 C、 D、

查看试题解析
6. 设 $a$ ， $b$ 是实数，定义一种新运算： $a * b = {(a - b)}^{2}$ ，下面有四个推断：
$① a * b = b * a$ ；
$② {(a * b)}^{2} = a^{2} * b^{2}$ ；
$③ (- a) * b = a * (- b)$ ；
$④ a * (b + c) = a * b + a * c$ ．
其中所有正确推断的序号是（）

A、 $① ② ③ ④$ B、 $① ③ ④$ C、 $① ②$ D、 $① ③$

查看试题解析
7. 若定义一种新的运算 $m Δ n = \frac{m + n}{1 + m n}$ ，例如： $3 Δ 2 = \frac{3 + 2}{1 + 3 \times 2} = \frac{5}{7}$ ，计算 $(- 5 Δ 2) Δ \frac{1}{3}$ 的结果为（）

A、 $\frac{3}{5}$ B、 $- \frac{3}{5}$ C、 $\frac{2}{7}$ D、 $- \frac{2}{7}$

查看试题解析
8. 定义一种新运算：当 $a > b$ 时， $a * b = a b + b$ ；当 $a < b$ 时， $a * b = a b - b$ ．若 $3 * (x + 2) > 0$ ，则x的取值范围是（）

A、 $- 1 < x < 1$ 或 $x < - 2$ B、 $x < - 2$ 或 $1 < x < 2$ C、 $- 2 < x < 1$ 或 $x > 1$ D、 $x < - 2$ 或 $x > 2$

查看试题解析
9. 对代数式 $A$ 定义新运算： $\sqrt{A^{2}} = | A |$ ．在代数式 $a + b + c$ 中任意加新运算，然后按给出的运算顺序重新运算，称此为“新运算操作”．实数 $a$ ， $b$ ， $c$ 在数轴上的位置如图所示．例如： $a + \sqrt{b^{2}} + c = a + | b | + c = a - b + c$ ， $\sqrt{a^{2}} + \sqrt{{(b + c)}^{2}} = | a | + | b + c | = a - b - c$ ， $⋯$ ．下列说法正确的个数是（）
① $\sqrt{a^{2}} + b + \sqrt{c^{2}} > 0$ ；
② $a + \sqrt{{(b + c)}^{2}} = a + \sqrt{b^{2}} + \sqrt{c^{2}}$ ；
③至少存在一种“新运算操作”，使运算结果与原代数式之和为0；
④至少存在一种“新运算操作”，使运算结果为 $- a - b + c$ ．

A、4 B、3 C、2 D、1

查看试题解析
10. 对于任意实数m，n，若定义新运算 $m \otimes n = {\begin{array}{l} \sqrt{m} - \sqrt{n} (m \geq n) ， \\ \sqrt{m} + \sqrt{n} (m < n) \end{array}$ ，给出三个说法：
① $18 \otimes 2 = 2 \sqrt{2}$ ；② $\frac{1}{1 \otimes 2} + \frac{1}{2 \otimes 3} + \frac{1}{3 \otimes 4} + \cdot \cdot \cdot + \frac{1}{99 \otimes 100} = 100 \otimes 1$ ；③ $(a \otimes b) \cdot (b \otimes a) = | a - b |$ ．
以上说法中正确的个数是（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
11. 定义符号min{a，b}的含义为：当a≥b时， min{a，b}=b；当a<b时，min{a，b}=a.如：min{1，-3}=-3，min{-4，-2}=-4.已知一种关于x的新函数y=min{x+1，-x+m}，且m>-1，则关于y的函数下面说法错误的是（）.

A、若m=1，则当y≤-2时，则x≤-3或x≥3 B、当函数图象经过(0， $\frac{1}{2}$ )时，该函数图象的最高点的坐标为( $- \frac{1}{4}$ ， $\frac{3}{4}$ ) C、( $\frac{m}{2}$ ， y₁) ( $\frac{m + 1}{2}$ ， y₂)是函数图象上的两点，则y₁>y₂ D、当1≤x≤2时，函数y的最大值为3，则m=3或5

查看试题解析
12. 在平面直角坐标系中，对于点 $P (x, y)$ ，把点 $P_{1} (y, \frac{1}{1 - x})$ 叫做点 $P$ 的友好点．已知点 $A_{1}$ 的友好点为点 $A_{2}$ ，点 $A_{2}$ 的友好点为点 $A_{3} ⋯$ 这样依次得到点 $A_{1}, A_{2}, A_{3}, A_{4} ⋯ A_{x}$ ，若点 $A_{1}$ 的坐标为 $(\frac{1}{2}, 2)$ ，则根据友好点的定义，点 $A_{2023}$ 的坐标为（）

A、 $(\frac{1}{2}, 2)$ B、 $(2, - 1)$ C、 $(- 1, - 1)$ D、 $(- 1, \frac{1}{2})$

查看试题解析
13. 定义一种对正整数 $n$ 的“ $F$ ”运算：①当 $n$ 为奇数时， $F (n) = 5 n + 3$ ；②当 $n$ 为偶数时， $F (n) = \frac{n}{2^{k}}$ （其中， $k$ 是使 $F (n)$ 为奇数的正整数）， $\dots \dots$ ，两种运算交替重复进行，例如，取 $n = 20$ ，则运算过程如图所示：若 $n = 3$ ，则第2023次“ $F$ ”运算的结果是（）

A、3 B、9 C、18 D、48

查看试题解析
14. 定义：在平面直角坐标系中，对于点P（x₁ ， y₁），当点Q（x₂ ， y₂）满足2（x₁+x₂）＝y₁+y₂时，称点Q（x₂ ， y₂）是点P（x₁ ， y₁）的“倍增点”．已知点P₁（1，0），有下列结论：
①点Q₁（3，8），Q₂（﹣2，﹣2）都是点P₁的“倍增点”；
②若直线y＝x+2上的点A是点P₁的“倍增点”，则点A的坐标为（2，4）；
③抛物线y＝x²﹣2x﹣3上存在两个点是点P₁的“倍增点”；
④若点B是点P₁的“倍增点”，则P₁B的最小值是 $\frac{4 \sqrt{5}}{5}$ ；
其中，正确结论的个数是（　　）

A、1 B、2 C、3 D、4

查看试题解析
15. 定义：如果代数式 $A = a_{1} x^{2} + b_{1} x + c_{1} (a_{1} \neq 0 ， a_{1} ， b_{1} ， c_{1}$ 是常数 $)$ 与 $B = a_{2} x^{2} + b_{2} x + c_{2} (a_{2} \neq 0 ， a_{2} ， b_{2} ， c_{2}$ 是常数 $)$ ，满足 $a_{1} + a_{2} = 0$ ， $b_{1} = b_{2}$ ， $c_{1} + c_{2} = 0$ ，则称这两个代数式 $A$ 与 $B$ 互为“同心式”，下列四个结论：
$(1)$ 代数式： $- 3 x^{2} + 2 x$ 的“同心式”为 $3 x^{2} - 2 x$ ；
$(2)$ 若 $8 m x^{2} + n x - 5$ 与 $6 n x^{2} - 4 x + 5$ 互为“同心式”，则 $(m + n)^{2023}$ 的值为 $1$ ；
$(3)$ 当 $b_{1} = b_{2} = 0$ 时，无论 $x$ 取何值时，“同心式” $A$ 与 $B$ 的值始终互为相反数；
$(4)$ 若 $A$ 、 $B$ 互为“同心式”，且 $b_{1}^{2} - 36 a_{1} c_{1} = 0$ ，则 $A - 2 B = 0$ 有两个相等的实数根．
其中，正确的结论有个．（）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
16. 定义：如果代数式 $A = a_{1} x^{2} + b_{1} x + c_{1}$ ( $a_{1} \neq 0$ ， $a_{1}$ ， $b_{1}$ ， $c_{1}$ 是常数)与 $B = a_{2} x^{2} + b_{2} x + c_{2}$ ( $a_{2} \neq 0$ ， $a_{2}$ ， $b_{2}$ ， $c_{2}$ 是常数)，满足 $a_{1} + a_{2} = 0$ ， $b_{1} + b_{2} = 0$ ， $c_{1} + c_{2} = 0$ ，则称这两个代数式 $A$ 与 $B$ 互为“和谐式”，对于上述“和谐式” $A$ 、 $B$ ，下列三个结论正确的个数为（）
①若 $A = - x^{2} - \frac{4}{3} m x - 2$ ， $B = x^{2} - 2 n x + n$ ，则 $(m + n)^{2023}$ 的值为-1；
②若 $k$ 为常数，关于 $x$ 的方程 $A = k$ 与 $B = k$ 的解相同，则 $k = 0$ ；
③若 $p$ ， $q$ 为常数， $p A + q B$ 的最小值为 $p - q$ ，则 $A$ 有最小值，且最小值为1.

A、0个 B、1个 C、2个 D、3个

查看试题解析

二、填空题

17. 如果一个两位数a的个位数字与十位数字都不是零，且互不相同，我们称这个两位数为“英华数”，定义新运算：将一个“英华数”的个位数字与十位数字对调，把这个新两位数与原两位数的和与11的商记 $ω (a)$ ，例如：a=13，对调个位数字与十位数字得到新两位数31，新两位数与原两位数的和，31+13=44，和与11的商44÷11=4，所以 $ω (13) = 4$ ．根据以上定义，回答下列问题：

(1)、计算： $ω （ 27 ）$ ．

(2)、若m，n都是“英华数”，且m+n=100，则 $ω (m) + ω (n) =$ ．

查看试题解析
18. 对 $x$ ， $y$ 定义一种新运算 $F$ ，规定： $F (x ， y) = (m x + n y) (3 x - y)$ （其中 $m$ ， $n$ 均为非零常数）.例如： $F (1 ， 1) = 2 m + 2 n$ ， $F (- 1 ， 0) = 3 m$ .当 $F (1 ， - 1) = - 8$ ， $F (1 ， 2) = 13$ ，则 $F (x ， y) =$ ；当 $x^{2} \neq y^{2}$ 时， $F (x ， y) = F (y ， x)$ 对任意有理数 $x$ ， $y$ 都成立，则 $m$ ， $n$ 满足的关系式是.

查看试题解析
19. 对实数 $a$ 、 $b$ ，定义运算☆如下： $a$ ☆ $b =$ ${\begin{array}{l} a^{b} (a ＞ b ， a \neq 0 ） \\ a^{- b} (a \leq b ， a \neq 0 ）， \end{array}$ ，
例如2☆3= $2^{- 3} = \frac{1}{8}$ .计算[2☆( $- 4$ )] $\times$ [( $- 4$ )☆( $- 2$ )]=

查看试题解析
20. 定义： $Φ [a ， b ， c]$ 是以 $a$ 、 $b$ 、 $c$ 为系数的二次多项式，即 $Φ [a ， b ， c] = a x^{2} + b x + c$ ，其中 $a$ 、 $b$ 、 $c$ 均为实数 $.$ 例如 $Φ [1，2 ， 3] = x^{2} + 2 x + 3$ 、 $Φ [2，0 ， - 2] = 2 x^{2} - 2$ ．
$①$ 当 $x = 2$ 时，求 $Φ [1，1 ， 1] \times Φ [- 1 ， - 1 ， - 1] =$ ；
$②$ 若 $Φ [p ， q ， - 1] \times Φ [m ， n ， - 2] = 2 x^{4} + x^{3} - 10 x^{2} - x + 2$ ，求 $(4 p - 2 q - 1) (2 m - n - 1) =$ ．

查看试题解析

三、解答题

21. 对于特殊四边形，通常从定义、性质、判定、应用等方面进行研究，我们借助于这种研究的过程与方法来研究一种新的四边形——筝形．
定义：在四边形 $A B C D$ 中，若 $A B = A D ， B C = C D$ ，我们把这样四边形 $A B C D$ 称为筝形．
性质：按下列分类用文字语言填写相应的性质：
从对称性看：筝形是一个轴对称图形，它的对称轴是；
从边看：筝形有两组邻边分别相等；
从角看：；
从对角线看：．
判定：按要求用文字语言填写相应的判定方法，补全图形，并完成方法2的证明．
方法1：从边看：运用筝形的定义；
方法2：从对角线看：；
如图，四边形 $A B C D$ 中，．求证：四边形 $A B C D$ 是筝形．
应用：如图，探索筝形 $A B C D$ 的面积公式（直接写出结论）．

查看试题解析
22. 已如有理数 $a (a \neq 1)$ ，定义 $\frac{1}{1 - a}$ 为a的差倒数，如 $- 1$ 的差倒数为 $\frac{1}{1 - (- 1)} = \frac{1}{2}$ ．

(1)、 $- 3$ 的差倒数为；

(2)、如果 $a_{1} = - 1$ ， $a_{2}$ 是 $a_{1}$ 的差倒数． $a_{3}$ 是 $a_{2}$ 的差倒数……，依此类推．求 $a_{1} + a_{2} + a_{3} + \cdot \cdot \cdot + a_{2024}$ 的值．

查看试题解析
23. 对于整数n ，定义[ $\sqrt{n}$ ]为不大于 $\sqrt{n}$ 的最大整数，例如：[ $\sqrt{3}$ ]＝1，[ $\sqrt{4}$ ]＝2，[ $\sqrt{5}$ ]＝2．

(1)、直接写出[ $\sqrt{10}$ ]的值；

(2)、显然，当[ $\sqrt{n}$ ]＝1时，n＝1，2或3．
①当[ $\sqrt{n}$ ]＝2时，直接写出满足条件的n的值；
②当[ $\sqrt{n}$ ]＝10时，求满足条件的n的个数；

(3)、对72进行如下操作：72 $\overset{第一次}{\to}$ [ $\sqrt{72}$ ]＝8 $\overset{第二次}{\to}$ [ $\sqrt{8}$ ]＝2 $\overset{第三次}{\to}$ [ $\sqrt{2}$ ]＝1，即对72进行3次操作后变为1，类似地：①对25进行 ▲ 次操作后变为2；
②对整数m进行3次操作后变为2，直接写出m的最大值．

查看试题解析
24. 在数轴上，点O表示的数为0，点M表示的数为m（m≠0）．给出如下定义：对于该数轴上的一点P与线段OM上一点Q，如果线段PQ的长度有最大值，那么称这个最大值为点P与线段OM的“闭距离”．如图1，若m＝－1，点P表示的数为3，当点Q与点M重合时，线段PQ的长最大，值是4，则点P与线段OM的“闭距离”为4．

(1)、如图2，在该数轴上，点A表示的数为－1，点B表示的数为2．
①当m＝1时，点A与线段OM的“闭距离”为；
②若点B与线段OM的“闭距离”为3，求m的值；

(2)、在该数轴上，点C表示的数为－m，点D表示的数为－m＋3，若线段CD上存在点G，使得点G与线段OM的“闭距离”为5，直接写出m的最大值与最小值．

查看试题解析
25. 新定义：若无理数 $\sqrt{T}$ 的被开方数 $T$ （ $T$ 为正整数）满足 $n^{2} < T < (n + 1)^{2}$ （其中 $n$ 为正整数），则称无理数 $\sqrt{T}$ 的“青一区间”为 $(n ， n + 1)$ ；同理规定无理数 $- \sqrt{T}$ 的“青一区间”为 $(- n - 1 ， - n)$ ．例如：因为 $1^{2} < 2 < 2^{2}$ ，所以 $1 < \sqrt{2} < 2$ ，所以 $\sqrt{2}$ 的“青一区间”为 $(1 ， 2)$ ， $- \sqrt{2}$ 的“青一区间”为 $(- 2 ， - 1)$ ．请解答下列问题：

(1)、 $\sqrt{17}$ 的“青一区间”是； $- \sqrt{23}$ 的“青一区间”是；

(2)、若无理数 $- \sqrt{a}$ （ $a$ 为正整数）的“青一区间”为 $(- 3 ， - 2)$ ， $\sqrt{a + 3}$ 的“青一区间”为 $(3 ， 4)$ ，求 $\sqrt[3]{a + 1}$ 的值；

(3)、实数x ， y ， m满足关系式： $\sqrt{2 x + 3 y - m} + \sqrt{3 x + 4 y - 2 m} = \sqrt{x + y - 2023} + \sqrt{2023 - x - y}$ ，求 $m$ 的算术平方根的“青一区间”．

查看试题解析
26. 对于正数 $x$ ，用符号 $[x]$ 表示 $x$ 的整数部分，例如 $[0.1] = 0$ ， $[2.5] = 2$ ， $[3] = 3 .$ 点 $A (a ， b)$ 在第一象限内，以 $A$ 为对角线的交点画一个矩形，使它的边分别与两坐标轴垂直 $.$ 其中垂直于 $y$ 轴的边长为 $a$ ，垂直于 $x$ 轴的边长为 $[b] + 1$ ，那么，把这个矩形覆盖的区域叫做点 $A$ 的矩形域 $.$ 例如：点 $(3 ， \frac{3}{2})$ 的矩形域是一个以 $(3 ， \frac{3}{2})$ 为对角线交点，长为 $3$ ，宽为 $2$ 的矩形所覆盖的区域，如图 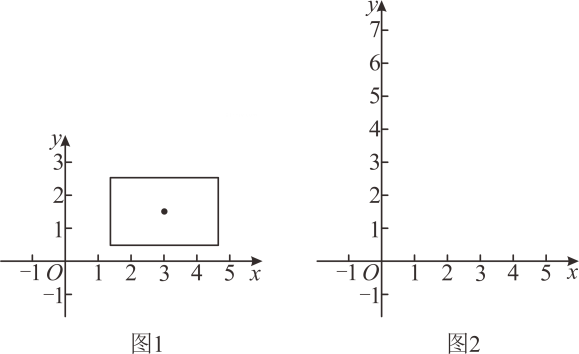$1$ 所示，它的面积是 $6$ ．
根据上面的定义，回答下列问题：

(1)、在图 $2$ 所示的坐标系中画出点 $(2 ， \frac{7}{2})$ 的矩形域，该矩形域的面积是；

(2)、点 $P (2 ， \frac{7}{2})$ ， $Q (a ， \frac{7}{2}) (a > 0)$ 的矩形域重叠部分面积为 $1$ ，则 $a$ 的值为．

查看试题解析
27. 定义：如果一个数的平方等于 $- 1$ ，记为 $i^{2} = - 1$ ，这个数 $i$ 叫做虚数单位，那么和我们所学的实数对应起来就叫做复数，表示为 $a + b i$ （a ， b为实数），a叫做这个复数的实部，b叫做这个复数的虚部，它的加、减、乘法运算与整式的加、减、乘法运算类似．例如计算： $(2 + i) + (3 - 4 i) = (2 + 3) + (i - 4 i) = 5 - 3 i$ ．

(1)、填空： $i^{3} =$ ； $i^{4} =$ ．

(2)、填空：① $(3 + i) (3 - i) =$ ；② ${(5 + i)}^{2} =$ ．

(3)、若两个复数相等，则它们的实部和虚部必须分别相等，完成下题：已知 $x + 4 i = (2 - x) - y i$ （x ， y为实数），求x、y的值．

查看试题解析
28. 我们知道，任意一个正整数n都可以进行这样的分解：n=p×q（p，q是正整数，且p≤q），在n的所有这种分解中，如果p，q两因数之差的绝对值最小，我们就称p×q是n的最佳分解．并规定：F（n）= $\frac{p}{q}$ ．
例如12可以分解成1×12，2×6或3×4，因为12﹣1＞6﹣2＞4﹣3，所以3×4是12的最佳分解，所以F（12）= $\frac{3}{4}$ ．
（Ⅰ）如果一个正整数m是另外一个正整数n的平方，我们称正整数m是完全平方数．
求证：对任意一个完全平方数m，总有F（m）=1；
（Ⅱ）如果一个两位正整数t，t=10x+y（1≤x≤y≤9，x，y为自然数），交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为36，那么我们称这个数t为“吉祥数”，求所有“吉祥数”；
（Ⅲ）在（2）所得“吉祥数”中，求F（t）的最大值．

查看试题解析